역시 이런 류는 icml 이지..
대부분의 sharpness 연구들은 scale dependency problem 이 있다. #126
요 문제를 해결하는 metric 들이 제안되었는데, (1, 2, 3, 4)
metric들을 제안한 paper들이 직접 학습들을 돌려보고 하지는 않았다.
3개의 contribution.
Adaptive Sharpness 제안
stronger correlation with generalization than sharpness does
adaptive sharpness를 활용한 learning 방법 제안
weight scale 에 따라 region을 maximization 하는 쪽으로 학습을 시킴
실험적으로 증명
SAM
SAM(#127) 설명은 생략.
SAM 결론만 살펴보면 다음과 같다.
ASAM
A가 loss function을 바꾸지 않는 scaling operator라고 할 때, (#126 참고)
분명 loss contour 등고선 간의 region 이 좁아질 수 있는데, 이럴 때도, $\rho$ 값이 유지되는건 문제가 있다.
우선 Normalization operator 를 정의한다.
${\huge Tw, w \in \mathbb{R}^k}$ 가 invertible linear operator 들이라고 놓자. given weight $w$ 에 대해 loss function을 건들이지 않고 ${\huge T^{-1}{Aw}A = T^{-1}_w}$ 이라면 ${\huge T^{-1}_w}$ 를 normalization operator 라고 하자.
Adaptive sharpness 는 다음과 같다.
논문에서 증명한 properties 까지 담고 있는 식.
결국, sharpness 값이 transformation 과 무관하게, 일정하게 나오게 만들어 준다는 것이다.
$w = (1, 1)$ 에 scaling operator $A=diag(3, 1/3)$ 을 곱해서 $w^{'} = (3, 1/3)$ 가 나왔다 가정하자.
파란색 line 위의 w 기준으로 SAM 에서처럼 $\max{L(w+\epsilon)}$에 해당하는 $\epsilon$ 값을 구해서 weight 를 구하고, Transforms들을 적용하면서, 빨간 line 을 그린다.
제안하는 방법은 epsilon ball 에도 transform 이 적용이 된다. (그림 참고)
generalization gap 은 mini-batch size, initial learning rate, weight decay coefficient, dropout rate 4개를 변경해 보면서, generalization gap 을 측정했다.
정의한 adaptive sharpness 와 correleation 을 찍어보면 유의미하다.
paper code
역시 이런 류는 icml 이지.. 대부분의 sharpness 연구들은 scale dependency problem 이 있다. #126 요 문제를 해결하는 metric 들이 제안되었는데, (1, 2, 3, 4) metric들을 제안한 paper들이 직접 학습들을 돌려보고 하지는 않았다.
3개의 contribution.
SAM
SAM(#127) 설명은 생략. SAM 결론만 살펴보면 다음과 같다.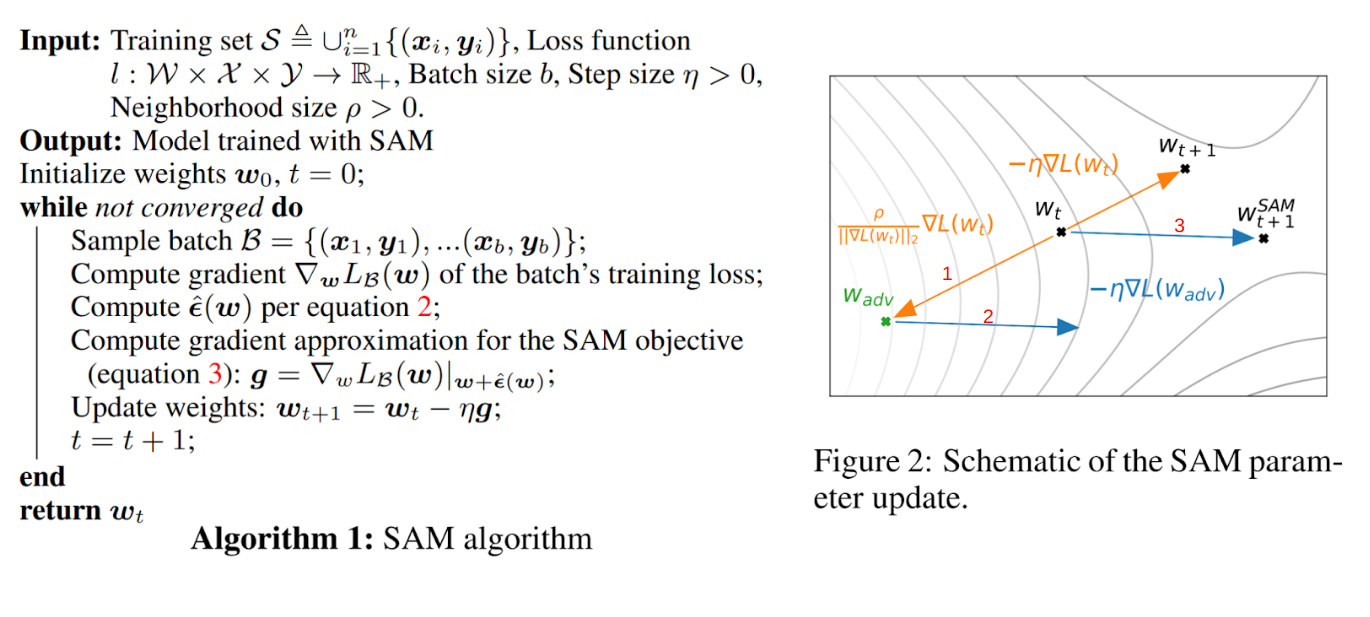
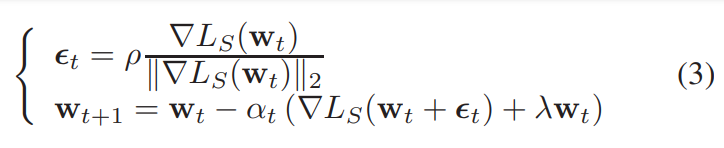
ASAM
A가 loss function을 바꾸지 않는 scaling operator라고 할 때, (#126 참고) 분명 loss contour 등고선 간의 region 이 좁아질 수 있는데, 이럴 때도, $\rho$ 값이 유지되는건 문제가 있다.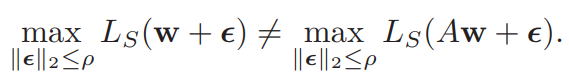
우선 Normalization operator 를 정의한다. ${\huge Tw, w \in \mathbb{R}^k}$ 가 invertible linear operator 들이라고 놓자. given weight $w$ 에 대해 loss function을 건들이지 않고 ${\huge T^{-1}{Aw}A = T^{-1}_w}$ 이라면 ${\huge T^{-1}_w}$ 를 normalization operator 라고 하자.
이를 만족시키는 $T_w$ 는 다음 두개를 써 볼 수 있다.
실제로 $T_w$ 를 계산할 때는, 안정성을 위해 $T_w +ηI_k$ 형태로 작은 $η$ 를 함께 썼다. (0.05) https://github.com/SamsungLabs/ASAM/blob/f156a680171db16d551c0d85cba2514fa3bff6a2/asam.py#L24
Adaptive sharpness 는 다음과 같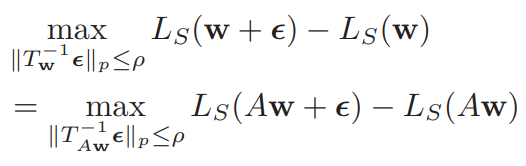다.
논문에서 증명한 properties 까지 담고 있는 식.
결국, sharpness 값이 transformation 과 무관하게, 일정하게 나오게 만들어 준다는 것이다.
$w = (1, 1)$ 에 scaling operator $A=diag(3, 1/3)$ 을 곱해서 $w^{'} = (3, 1/3)$ 가 나왔다 가정하자. 파란색 line 위의 w 기준으로 SAM 에서처럼 $\max{L(w+\epsilon)}$에 해당하는 $\epsilon$ 값을 구해서 weight 를 구하고, Transforms들을 적용하면서, 빨간 line 을 그린다.
제안하는 방법은 epsilon ball 에도 transform 이 적용이 된다. (그림 참고) generalization gap 은 mini-batch size, initial learning rate, weight decay coefficient, dropout rate 4개를 변경해 보면서, generalization gap 을 측정했다. 정의한 adaptive sharpness 와 correleation 을 찍어보면 유의미하다.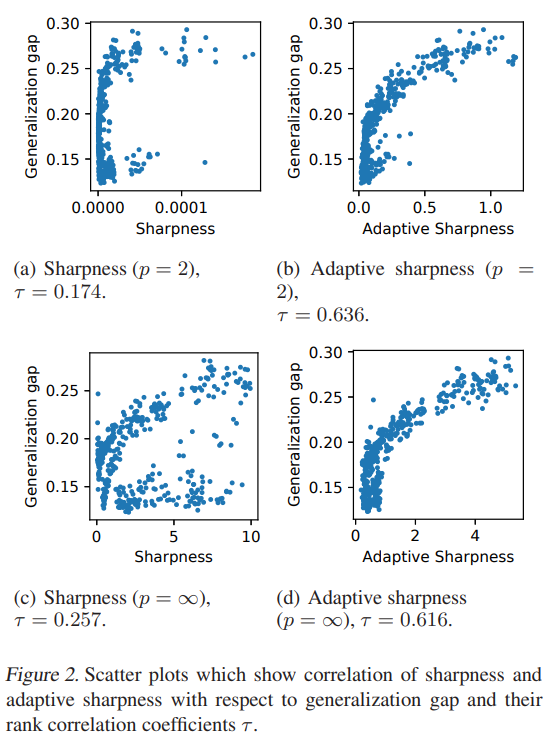
Adaptive Sharpness-Aware Minimization
그래서 minimization 은 어떻게 하냐.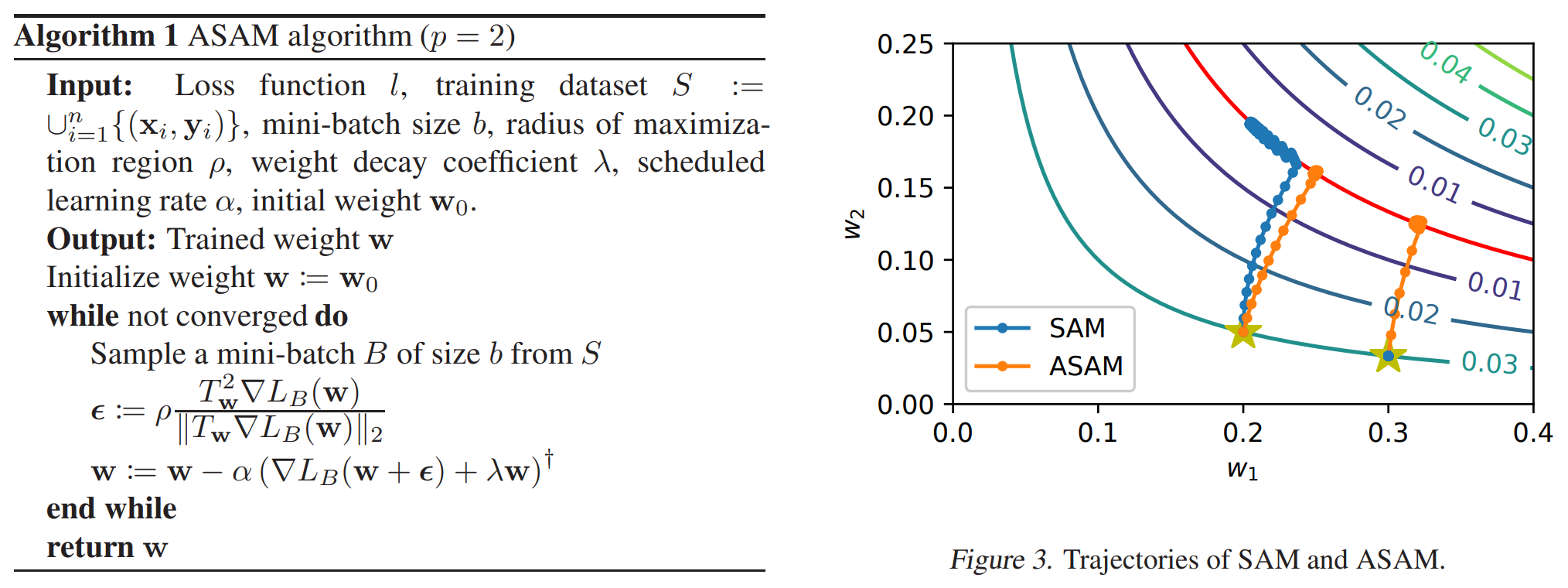
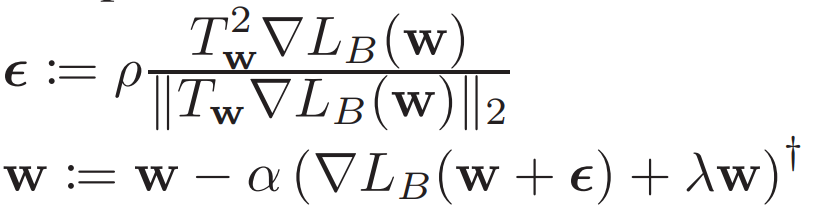
Results
norm 은 L2 쓰는게 좋다. $\rho$ 값은 여전히 hyperparameter.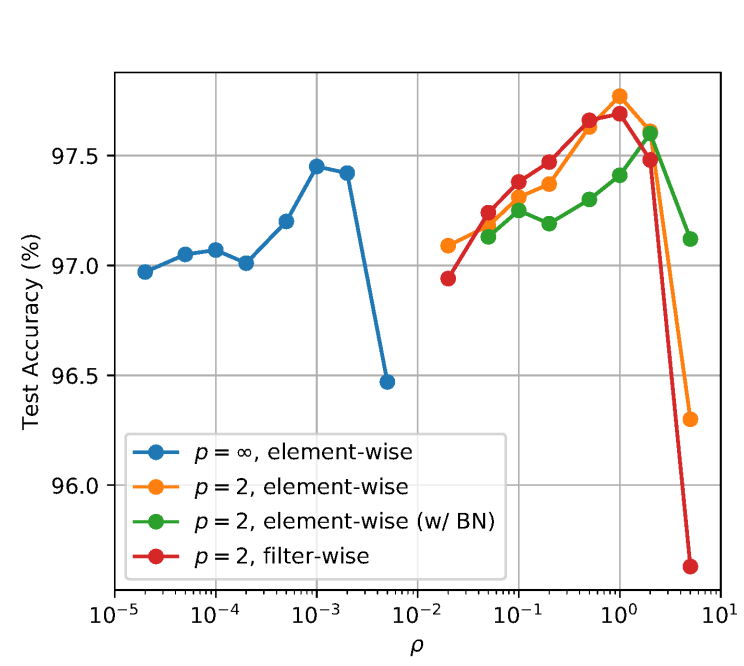
cifar-10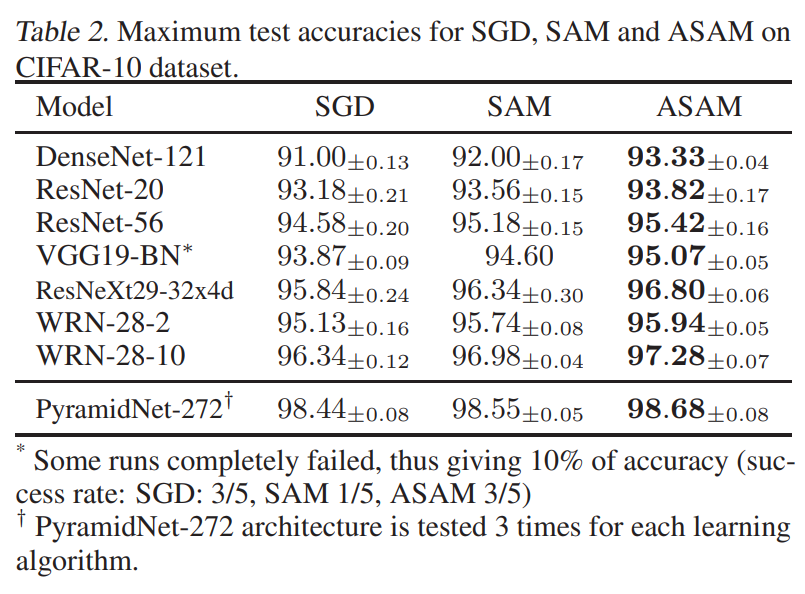
cifar-100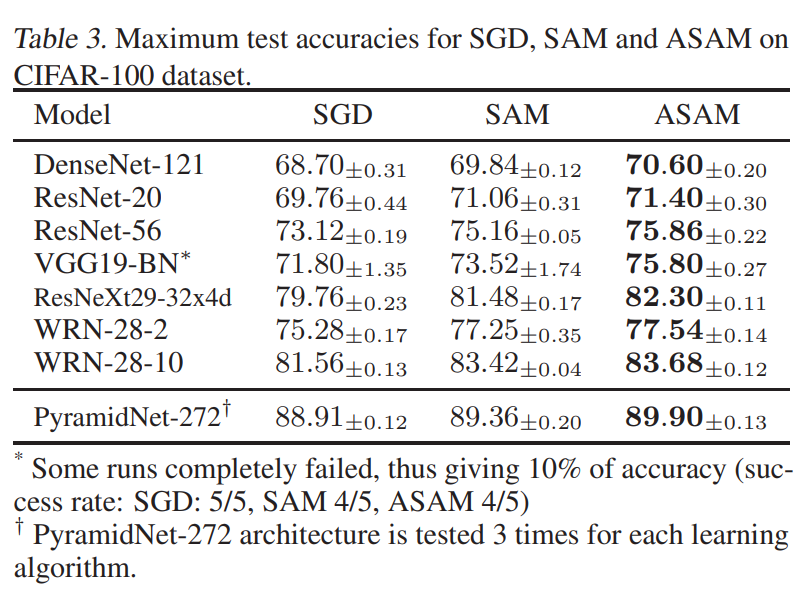
Imagenet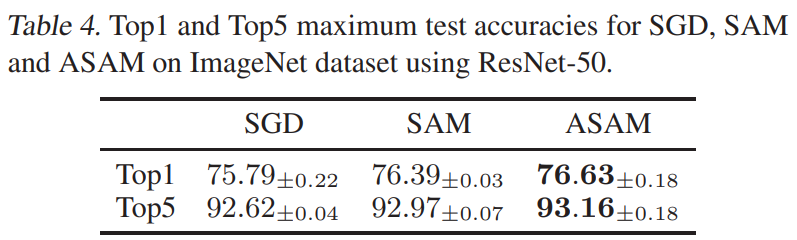
MNT (DE-EN)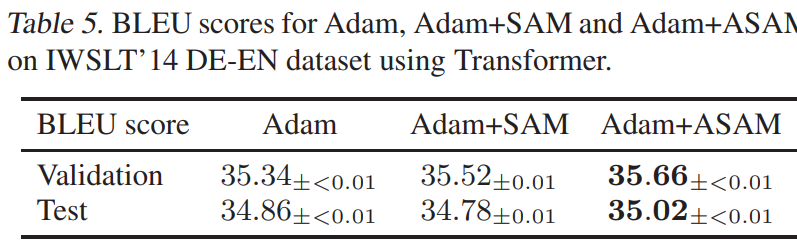
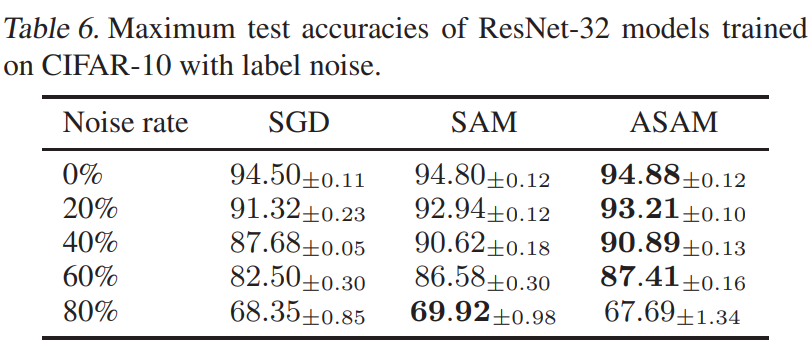
SAM 은 라벨 노이즈에 강인하다?