Taking point to point average

[htala]

Hi I was wondering does it make sense to take the average of the calculated force of a particular muscle of 17 subjects? I have normalized the forces of all subjects to 101 points and then used spm1d code to take the average but it seems like a point to point average is taken. The result makes me wonder if it makes sense at all.

Please correct me if I am wrong on how SPM1d take the average of multiple wave forms.

regards

[0todd0000]

Hello, you are correct regarding how SPM calculates means. Your question --- regarding whether this is appropriate --- is a very good one, as it gets right to the heart of SPM, and indeed highlights some important constraints regarding how SPM results should be interpreted.

Here is a short answer: Yes, computing means in this point-by-point manner makes sense, provided the data have been acceptably registered to a homologous domain.

where:

• "registered" means "time normalized" for these data, and is discussed further below
• "homologous" means "corresponding"
• "domain" means the measurement domain, in this case a one-dimensional time continuum

Here is a longer answer: Let's consider a conceptually simpler example first. Consider the temperature data in the figure below from Ramsay & Silverman (2005)

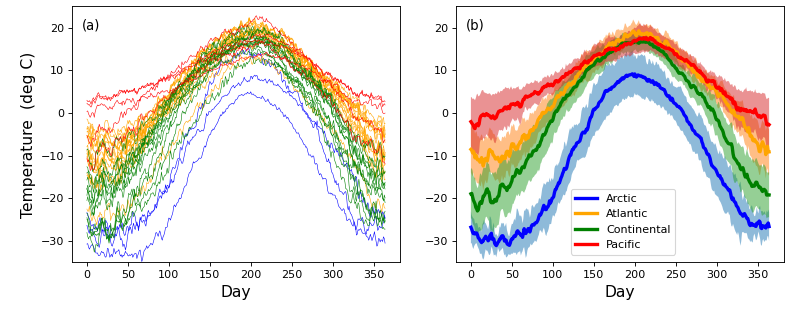
(Click here to see this figure in its original context.)

The left-hand panel depicts observations from multiple measurement stations in each of four geographical regions in Canada, where one observation was recorded each day for one year. The right-hand panel depicts within-region means with standard deviation clouds. For these data, does it make sense to calculate means on Jan.1, then Jan.2, then Jan.3, etc.? Perhaps, perhaps not. This is a judgment that the researcher must make.

The only thing we can say for sure is that calculating means (and standard deviations) imposes an assumption of data homology. In other words, if the data are not homologous, then means should not be calculated, and indeed no analysis should be performed at all. Note that this issue applies to all types of data, not just 1D (or nD) data.

For example, in the muscle force data you attached, one could calculate the mean of the maximum muscle forces (i.e., one maximum force value for each measurement). Are maximum muscle forces homologous? Perhaps, perhaps not. We know from Newton's second law of motion that maximum force is directly related only to maximum acceleration, but only if there are no other (changing) external forces. Since many muscles tend to exert forces on the same bodies, the maximum muscle force of a single muscle might not be have homologous physical meaning across multiple observations. How about physiological meaning? Maximum force appears to be a reasonable indicator of the physiological state of a muscle, but instantaneous muscle force is also affected by muscle length, rate-of-length-change, whether the muscle is shortening or lengthening, fatigue, etc. Thus maximum muscle forces across observations may not necessarily represent homologous physiological states. Regardless, we know that the literature commonly compares maximum forces. Does this make sense? Perhaps, perhaps not. Again, the only thing we can say for sure is that calculating means imposes an assumption of data homology.

Returning finally to your question, and to the 1D muscle force data you attached: does it make sense to calculate means at each point in normalized time? Perhaps, perhaps not. Like the weather data, and like maximum force values, calculating means imposes an assumption of data homology, and whether or not this assumption is appropriate is a judgment that the researcher must make.

Related to this issue is registration, a concept that is common for 2D and 3D data, as in image registration and volume registration, and applies equally to 1D data but is not very widely discussed in the biomechanics literature. From your description I gather that the muscle force data you attached were processed using linear registration (i.e., interpolated at N evenly-spaced nodes between the start and end times, separately for each 1D observation; in this case N=101). An alternative is to use nonlinear registration, where the N nodes tend not to be evenly spaced; when the nodes are unevenly spaced, time becomes warped. A wide variety of nonlinear registration algorithms exist for 1D data (e.g. Ramsay & Li 1998; Sadeghi et al., 2000; Wrobel et al. 2019; Zeng et al. 2019), including manual, nonlinear registration, and nonlinear registration of 1D data remains an active area of research. If you were to apply one of these nonlinear procedures to your data, one or more of these procedures may produce qualitatively better-looking means, likely with smaller standard deviations. But does a better-looking mean imply that computing means makes sense? Perhaps, perhaps not. All we can say for sure is that calculating means imposes an assumption of data homology, and it is up to us as researchers to judge whether that assumption is appropriate.

Your question therefore highlights an important bottleneck in SPM results interpretation: If it does indeed make sense to calculate means, then by definition it also makes sense to calculate standard deviations, t and F and other test statistics, and probability values. In contrast, if it does not make sense to calculate means, presumably because the data cannot be regarded as homologous, then none of the other calculations should be performed.

As a general analysis approach, it would be advisable to apply a variety of registration techniques (including both linear and nonlinear registration), and to qualitatively evaluate the effects on the corresponding SPM results, and possibly also on means themselves. If there is little qualitative difference amongst the varying techniques' results, then the results can be deemed to be robust to the various assumptions of the various techniques. If, however, qualitative differences are identified, then one should probe the data to ensure they understand why those qualitative differences have emerged.

Last, as general rules-of-thumb for interpretation:

• Statistical results following linear registration embody both amplitude and morphology effects, where "morphology effects" means "timing effects" if the 1D domain is time.
• Statistical results following nonlinear registration embody primarily amplitude effects. That is, nonlinear registration procedures tend to minimize timing variability amongst multiple 1D measurements.
• By extension, if the overall statistical effects become markedly reduced following nonlinear registration, relative to the effects following linear registration, this implies that the linear registration results are caused primarily by morphology effects and not amplitude effects.

References

Ramsay JO, Li X (1998). “Curve registration.” Journal of the Royal Statistical Society Series B.

Ramsay JO, Silverman BW (2005). Functional Data Analysis Springer-Verlag, New York.

Sadeghi H, Allard P, Shafie K, Mathieu P, Sadeghi S, Prince F, Ramsay J (2000). “Reduction of gait data variability using curve registration.” Gait and Posture, 12(3), 257–264.

Wrobel J, Zipunnikov V, Schrack J, Goldsmith J (2019). “Registration for exponential family functional data.” Biometrics, 75(1), 48–57.

Zeng P, Qing SJ, Kim WS (2019). “Simultaneous Registration and Clustering for Multi- dimensional Functional Data.” Journal of Computational and Graphical Statistics, 1, 1–32.