Thanks for the isolation of that issue with a small subset of data.
That issue here again is the cascading of construction, using an inexact arithmetic. Here by inserting the segments several time, you just worsen the situation.
The good news is that the patch introduced in CGAL-4.11.2 and CGAL-4.11.3 can be reused. By default, it snap newly constructed points to existing points with a distance of 4 ULP (ignoring between 2 and 3 bits of precision). You can add the following line:
#define CGAL_CDT_2_INTERSECTION_SNAPPING_ULP_DISTANCE 8at the top of your .cpp file, and it will use that distance 8 instead of 4, ignoring between 3 and 4 bits of precision. And that fixes your test case. Maybe with your real data you will need a bigger value. Each time you double that value, you ignore one more bit of precision (among the 53 bits of precision of the double type).
Updated Issue Details, @lrineau 2018/08/02
The following test case should not loop, because it uses CDT_plus_2, that should prevent the insertion of twice the same constraint. See https://github.com/CGAL/cgal/issues/3267#issuecomment-409906745.
The old title was: [Probable infinite loop] Constrained 2D Delaunay triangulation : inserting a set of constraints takes forever
Issue Details
CGAL 4.11.3 introcuded a problem in the following code snippet (it was not present with previous releases (tested 4.11, 4.11.1, 4.11.2)). Inserting a constraint causes the insert_constraint method to never return.
The set of constraints are shown in the picture below: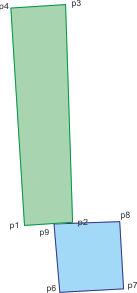
Source Code
I admit the use case is a bit contrived (inserting twice the same data). I don't know how to generate it in a simpler manner. I figured it was still worth submitting it.
Environment