first off all I have to admit that this is a very nicely documented issue 👍
Indeed I can reproduce it...
I'm wondering whether these values are way too small: νh=1e-3 κh=2e-3
Is these the values you intended or is there a typo here?
Closed Yesse42 closed 4 years ago
first off all I have to admit that this is a very nicely documented issue 👍
Indeed I can reproduce it...
I'm wondering whether these values are way too small: νh=1e-3 κh=2e-3
Is these the values you intended or is there a typo here?
I took those values from the Model Setup-Turbulent diffusivity closures and large eddy simulation models-constant anisotropic diffusivity section of the documentation. Probably should have sanity checked them beforehand.
julia> using Oceananigans.TurbulenceClosures
julia> closure = AnisotropicDiffusivity(νh=1e-3, νz=5e-2, κh=2e-3, κz=1e-1) AnisotropicDiffusivity: (νx=0.001, νy=0.001, νz=0.05), (κx=0.002, κy=0.002, κz=0.1)
Taking a look at my textbook, both the diffusivities look too small for the real world, especially the horizontal κh, as you mentioned. If I'm not mistaken, eddy diffusivity is much greater in magnitude than molecular diffusivity (and therefore more important), with typical vertical values of 10^-5 m^2/s, and horizontal eddy diffusivities range anywhere from 1m^2/sec to 10^4 m^2/sec. The kinematic viscosity νh=1e-3 looks to be much too big, though, with typical values ranging from 1.8 *10^-6 m^2/sec at 0ºC to 1.0*10^-6 m^2/ sec at 20ºC.
However, substituting those measured values in results in an even more fantastic blowup than before:

Substituting in a larger value (1) for the kinematic viscosity while keeping the above eddy diffusivities also leads to mayhem:

I should also note that the simulation issues happening in areas of strong temperature contrast are not exclusive to this specific kind of simulation. Even a simple wind stress simulation I tried to set up earlier with a fairly normal thermocline exhibits bizarre behavior at it (you'll probably have to view the gif frame by frame):

Given the above results, it seems like it may be something other than the anisotropic diffusivity messing things up.
You start with a very unstable stratification so you set up Rayleigh-Taylor instability. The reason you get inf temp is because simulation blows up. If I reduce the time-step I can integrate up to the final time of t=80sec that you chose, but if you need to integrate further probably you need to reduce the time-step further or add a time-step wizard...
I enhanced your script a bit with a log message to keep track of the CFL... I also added RK3 time-step. I also reduced the resolution to 128^3 so I can experiment as my laptop cannot casually run 256^3 simulations :)
using Oceananigans
using Oceananigans.OutputWriters, Oceananigans.Fields
using Oceananigans.Utils:day, hour, minute, second
grid1 = RegularCartesianGrid(size=(128, 128, 128), y=(-500, 500), x=(-500, 500), z=(-500, 0),topology = (Periodic, Periodic, Bounded))
model1=IncompressibleModel(grid=grid1,architecture = CPU(),float_type=Float64,clock = Clock(time=0.0),coriolis = BetaPlane(rotation_rate=7.292115e-5, latitude=0, radius=6371e3), timestepper = :RungeKutta3,
tracers=(:T, :S),buoyancy=SeawaterBuoyancy(),closure=AnisotropicDiffusivity(νh=1e-3, νz=5e-2, κh=2e-3, κz=1e-1))
@inline thermoc(x, y, z) = 16-12*tanh((z+250)/10)+rand(Float64)
@inline sal(x, y, z) = 16+12*tanh((z+250)/10)+rand(Float64)
set!(model1, u=-0.05, v=0, T=thermoc, S=sal)
using Oceananigans.Diagnostics: AdvectiveCFL
CFL = AdvectiveCFL(wizard)
start_time = time_ns()
progress(sim) = @printf("i: % 6d, sim time: % 10s, wall time: % 10s, Δt: % 10s, CFL: %.2e\n",
sim.model.clock.iteration,
prettytime(sim.model.clock.time),
prettytime(1e-9 * (time_ns() - start_time)),
prettytime(sim.Δt),
CFL(sim.model))
simulation = Simulation(model1, Δt=2., stop_time=80second, iteration_interval=4, progress=progress)
function init_save_some_metadata!(file, model)
file["author"] = "oofs"
return nothing
end
simulation.output_writers[:tracers] = JLD2OutputWriter(model1, model1.tracers,
prefix = "Temp Data",
schedule = TimeInterval(10second),
init = init_save_some_metadata!)
run!(simulation)
using Plots, JLD2, Printf, Oceananigans.Grids
x, y, z = nodes(model1.tracers.T)
file = jldopen(simulation.output_writers[:tracers].filepath)
iterations = parse.(Int, keys(file["timeseries/t"]))
anim = @animate for (i, iter) in enumerate(iterations)
@info "Drawing frame $i from iteration $iter..."
Temp = transpose(file["timeseries/T/$iter"][125,:,:])
timeofthing=file["timeseries/t/$iter"]
display(Temp)
contourf(y, z, Temp, title = "Temperature Profile at x=14000, t=$timeofthing",levels = 0:1:30,linewidth=0,xlabel = "y",ylabel = "z",)
end
gif(anim, "10s Timestep INFINITE TEMPERATURE REPRODUCER.gif", fps = 1)You'll see that even with these choice of parameters the CFL hits the roof (i.e., 1) pretty quickly...
i: 4, sim time: 8 seconds, wall time: 1.886 seconds, Δt: 2 seconds, CFL: 1.19e-02
i: 8, sim time: 16 seconds, wall time: 3.566 seconds, Δt: 2 seconds, CFL: 1.99e-02
i: 12, sim time: 24 seconds, wall time: 5.212 seconds, Δt: 2 seconds, CFL: 4.20e-02
i: 16, sim time: 32 seconds, wall time: 6.747 seconds, Δt: 2 seconds, CFL: 8.67e-02
i: 20, sim time: 40 seconds, wall time: 8.323 seconds, Δt: 2 seconds, CFL: 1.66e-01
i: 24, sim time: 48 seconds, wall time: 9.797 seconds, Δt: 2 seconds, CFL: 3.15e-01
i: 28, sim time: 56 seconds, wall time: 11.313 seconds, Δt: 2 seconds, CFL: 5.50e-01
i: 32, sim time: 1.067 minutes, wall time: 12.921 seconds, Δt: 2 seconds, CFL: 8.26e-01
i: 36, sim time: 1.200 minutes, wall time: 14.460 seconds, Δt: 2 seconds, CFL: 1.01e+00
i: 40, sim time: 1.333 minutes, wall time: 16.043 seconds, Δt: 2 seconds, CFL: 1.08e+00
[ Info: Simulation is stopping. Model time 1.333 minutes has hit or exceeded simulation stop time 1.333 minutes.
[ Info: Drawing frame 1 from iteration 0...
I am new to Julia, Oceananigans, and computational fluid dynamics, so please forgive me if I missed something obvious or made a trivial mistake.I am new to Julia, Oceananigans, and computational fluid dynamics, so please forgive me if I missed something obvious or made a trivial mistake.
No aspect of computational fluid dynamics is trivial or obvious! :-D I'd like to echo @navidcy for the thoughtful and well-documented issue.
Your issue is numerical instability! This occurs either because the time step is too large, or because the physical problem cannot be resolved on the specified grid, which can cause energy to accumulate at the grid scale, eventually leading to blow up. This example may be exhibiting both. As @navidcy demonstrates, reducing the time-step allows for a few time-steps to be taken without blowing up. However, the scale of the physics --- a Rayleigh-Taylor-type gravitational instability --- still appears to be quite small. The characteristic scale of the turbulent motions that result from your initial condition depends on the diffusivities that are prescribed.
Taking a look at my textbook, both the diffusivities look too small for the real world, especially the horizontal κh, as you mentioned. If I'm not mistaken, eddy diffusivity is much greater in magnitude than molecular diffusivity (and therefore more important), with typical vertical values of 10^-5 m^2/s, and horizontal eddy diffusivities range anywhere from 1m^2/sec to 10^4 m^2/sec
The turbulent eddy diffusivity is a property of turbulence, and thus of the physical scenario being simulated. So we can't say whether certain values are too large or too small, especially for an initial value problem like this. The numbers you've cited are typical numbers used for large-scale oceanographic problems (motions with scales of 10s of kilometers or more). However, the problem you are trying to simulate is very small scale, with a domain just 500 meters in each direction. and grid spacing down to 2 meters. In addition, its unlikely that putting this problem on a beta plane will change your results, because the domain is too small and the velocities too large for the effect of beta to influence your dynamics.
What kind of problem would you like to simulate? Perhaps we can help define a mathematical problem that is both simulate-able, and serves as a reasonable approximation for the physics you would like to explore.
Here's a script for Rayleigh-Taylor that produces this movie:

using Plots
using JLD2
using Printf
using Oceananigans
using Oceananigans.Grids
using Oceananigans.Advection
using Oceananigans.OutputWriters
using Oceananigans.Fields
using Oceananigans.Utils
using Oceananigans.Diagnostics: AdvectiveCFL
grid = RegularCartesianGrid(size=(128, 1, 128),
x = (-64, 64),
y = (0, 1),
z = (-64, 64),
topology = (Periodic, Periodic, Bounded))
model = IncompressibleModel(grid = grid,
architecture = CPU(),
advection = UpwindBiasedThirdOrder(),
timestepper = :RungeKutta3,
tracers = :b,
buoyancy = BuoyancyTracer(),
closure = IsotropicDiffusivity(ν=1e-2, κ=1e-2))
# Initial condition for Rayleigh-Taylor instability
#
# Rayleigh-Taylor instability occurs when dense fluid accelerates
# into lighter fluid below due to gravitational forces.
#
# The growth rate of Rayleigh-Taylor instability is
#
# γ = √(k * Δb)
#
# where k is the wavenumber of the unstable mode and Δb is the jump from
# light to dense fluid (I've defined buoyancy such that Δb = - g * Δρ, where g
# is gravitational acceleration and Δρ is the density jump). The growth rate is faster
# for smaller modes, which means the smallest scale of the motions that develop depend
# either on the viscous scale, or, in a numerical simulation, the grid scale.
#
# The rate at which energy is removed at the grid scale is roughly
@show γ_diffusion = model.closure.κ.b / grid.Δx^2
# We choose the buoyancy jump so that the growth rate at the grid scale
# is (hopefully) affected significantly by molecular viscosity and diffusion
# (but one large enough to allow the simulation to run in a reasonable amount
# of time). The grid-scale wavenumber is
k = grid.Nx * 2π / grid.Lx
# And our target growth rate is
γ_growth = 100 * γ_diffusion
# which yields a buoyancy jump
Δb = γ_growth^2 / k
# We also choose the width of the buoyancy jump to be
d = 2 * grid.Δz # a bit above the grid scale
# Initial condition: unstable buoyancy gradient + noise
unstable_buoyancy(x, y, z) = - Δb * tanh(z / d) * (1 + 1e-2 * Δb * randn())
set!(model, b = unstable_buoyancy)
wizard = TimeStepWizard(cfl=1.0, Δt=0.2, max_Δt=1.0, max_change=1.1)
CFL = AdvectiveCFL(wizard)
start_time = time_ns()
progress(sim) = @printf("i: % 6d, sim time: % 10s, wall time: % 10s, Δt: % 10s, CFL: %.2e\n",
sim.model.clock.iteration,
prettytime(sim.model.clock.time),
prettytime(1e-9 * (time_ns() - start_time)),
prettytime(sim.Δt.Δt),
CFL(sim.model))
simulation = Simulation(model,
Δt = wizard,
stop_iteration = 200,
iteration_interval = 2,
progress = progress)
simulation.output_writers[:tracers] =
JLD2OutputWriter(model, model.tracers,
prefix = "rayleigh_taylor_instability",
schedule = IterationInterval(2),
force = true)
run!(simulation)
x, y, z = nodes(model.tracers.b)
file = jldopen(simulation.output_writers[:tracers].filepath)
iterations = parse.(Int, keys(file["timeseries/t"]))
anim = @animate for (i, iter) in enumerate(iterations)
@info "Drawing frame $i from iteration $iter..."
b = file["timeseries/b/$iter"][:, 1, :]
t = file["timeseries/t/$iter"]
bmin = -Δb
bmax = +Δb
blevels = range(bmin, bmax, length=31)
contourf(x, z, clamp.(b, bmin, bmax)',
title = @sprintf("buoyancy at t = %.2f", t),
colors = :thermal,
aspectratio = :equal,
xlim = (-grid.Lx/2, grid.Lx/2),
ylim = (-grid.Lz/2, grid.Lz/2),
levels = blevels,
linewidth = 0,
xlabel = "x",
ylabel = "z")
end
gif(anim, "rayleigh_taylor_instability.gif", fps = 8)Firstly, thanks to both of you for pointing out the importance of the CFL in maintaining realistic simulation results. Switching to a lower time step/ lower CFL timestep-wizard fixed my problems in some other simulations I was trying to run, such as one of Couette flow and an Ekman spiral. Both of the simulations suffered from massive CFLs. Also, thanks @navidcy for mentioning a reduced grid size. It made the simulations run in a more reasonable amount of time
Here's a gif from the Couette flow that had a horrifying CFL, but now works.

Also, the in depth description of Rayleigh-Taylor instability from @glwagner was quite interesting, and thanks for taking the time to show me how to properly set up a simulation of highly nonlinear dynamics such as this. I didn't realize that numerical instability was such a problem beforehand.
Lastly, thank you @glwagner for offering to help me set up a basic model, but for now I think all my issues have been fixed with other simulations I was trying thanks to the CFL advice, so those will suffice for now; still, thanks for the great help you've both already given. Thanks for all the work you put into Oceananigans too; it's quite fascinating and I can't wait to explore more.
@Yesse42, you might wanna have a look at: https://clima.github.io/OceananigansDocumentation/stable/model_setup/time_stepping/ on how to set up adaptive time-step.
(Note that with RK3 time-stepping could be "OK" to cap CFL at ~0.6 or 0.7.)
Hello! I am new to Julia, Oceananigans, and computational fluid dynamics, so please forgive me if I missed something obvious or made a trivial mistake.
As a first exercise with Oceananigans I am trying to simulate some high salinity, low temperature water above low salinity, high temperature water (with a bit of random noise), with a small initial westward velocity component and a 10 second time step. The documentation was quite helpful (thanks for that), and the simulation works as expected until about t=50s, when small water parcels at the density interface heat up or cool down to unnatural levels (see attached gifs at bottom), and occasionally the entire temperature matrix fills with NaN's. I've tried removing all my boundary conditions to see if they were the problem, but the issue persisted.
For reference, I am using Julia v1.5 with Oceananigans 0.44.1, with this platform: OS: macOS (x86_64-apple-darwin18.7.0) CPU: Intel(R) Core(TM) i5-6360U CPU @ 2.00GHz WORD_SIZE: 64 LIBM: libopenlibm LLVM: libLLVM-9.0.1 (ORCJIT, skylake).
And here is a minimal example, along with code to gif-ify the output. Lowering the timestep down to 1 second from the current 10 seconds also does not fix anything. Also using a time step wizard with initial del_t at 1 second and cfl=0.3 still generates unrealistic temperatures; however, it then seems to freeze before converting entirely to NaN's and would not progress given an extra (real-life) hour to run compared to the fixed timestep.
And here are some gifs showcasing the issue from the code above with slight modifications. I also forgot to change the name of my plots; they are centered in the x-direction, but are not at x=14000m. Sorry about that. 1 second timestep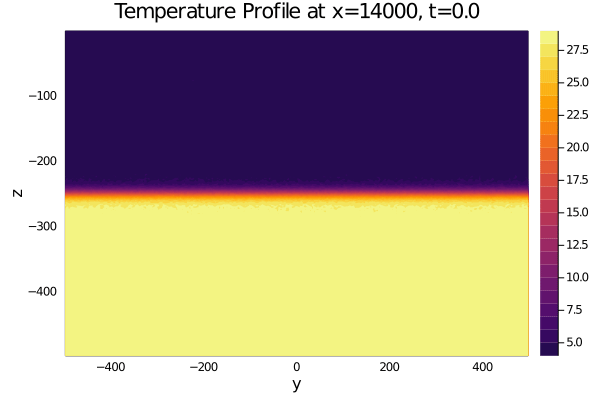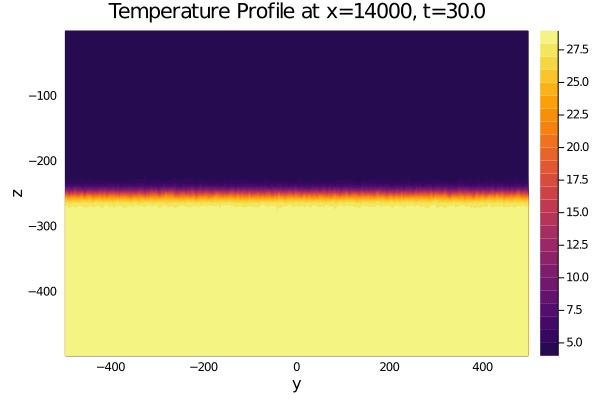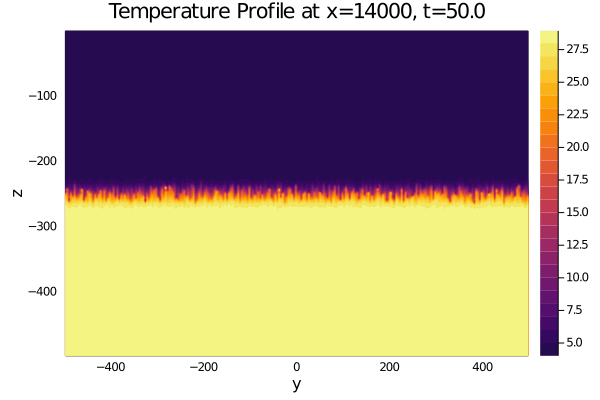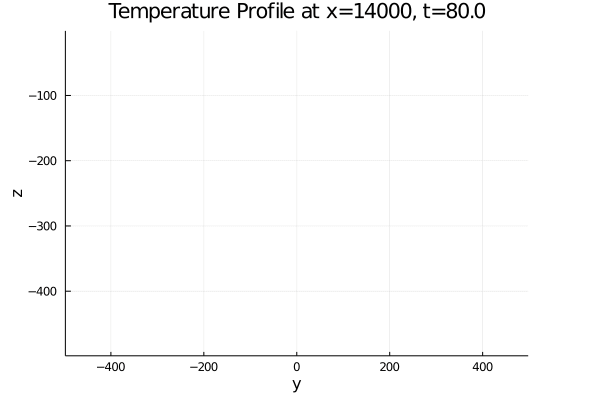
Initial 1 second timestep timestep wizard
10 second timestep (code exactly as written above)
Also do note that the 10 second solutions have run to run inconsistency in their bad behavior (probably due to the use of randomness to define the initial state).
I'm not sure if this is a considered a bug or just an artifact of an improper simulation setup, but thanks in advance for your help regardless!!