Open Doragd opened 10 months ago
港科大团队在Recsys23上提出了针对推荐系统中多兴趣召回问题的新策略。为应对select-interest-focused特性使现有负例采样策略失效和现有兴趣路由设计容易出现崩塌的挑战，作者提出难负例采样策略和路由正则化策略。这所带来的优化结果在实验证明了这些策略能有效提高推荐系统的性能，为推荐系统提供了新的优化视角。
多兴趣召回的核心是通过用户历史行为捕捉用户的多种兴趣表示，使用不同的兴趣表示进行多路兴趣感知的差异化并行召回。
从模型结构看，多兴趣召回需要结合用户画像特征和历史行为序列特征来生成item-to-interest的兴趣路由矩阵$A\in\mathbb{R}^{n\times K}$，其中$n$是历史行为序列的长度，$K$是用户兴趣head的数量。利用兴趣路由矩阵可以将item表示映射到具体的兴趣表示$V_u\in \mathbb{R}^{d \times K}$中，即$V_u=HA $，其中$H\in\mathbb{R}^{d \times n}$是用户历史行为序列中$n$个item的特征表示。这一部分的核心主要是怎么去学习一个好的兴趣路由矩阵。
从训练策略看，对于(user, target item)一对训练正样本，将多个兴趣表示与target item的兴趣表示计算相似度后，可以采用$\mathrm{argmax}$策略，得到与target item最相似的兴趣head表示作为user侧的表征$v_u\in\mathbb{R}^{d\times 1}$，即$k=\mathrm{argmax}{(V_u^Te^{i^+})}, v_u=V_u[:,k]$。随后，采用常规的交叉熵损失函数去优化：拉近user表征和target item之间的距离，同时排开负样本item，如下图所示。核心还是怎么去做负例的采样。
一般来说，采样有两种，全库均匀采样或者batch内采样。对于batch内采负例会面临着打压高热物料的问题，所以会有一个logQ消偏的方式。
至于serving策略，则是将$K$个兴趣表征分别作为user表征进行$K$路并行召回topN个item。
多兴趣召回在训练时采用的$\mathrm{argmax}$方式，选择最相似的兴趣head的表征作为user向量和target item向量构成一对正例pair进行训练，负样本则采用全库均匀采样或者batch内采样。尽管这种负采样方式采到的负例（如计算机、面包）对于由食品、电子产品等构成的用户历史行为序列而言是难负例，但是就特定兴趣的head（如书包）而言，这些难负例就会变成简单负例。因此，对于多兴趣召回这种select-interest-focused的训练方式，常见的负采样策略往往会失效。
作者也定量地分析了这一问题。REMI是作者提出的改进策略，PIMIRec和ComiRec则是经典的多兴趣召回策略。虚线表示四种策略采用全库softmax的方式（注：这里的全库相比工业界实际很小）的Recall@50，横轴则表示，采用Sampled Softmax方式时，负例的数量会严重影响模型的性能。考虑到工业届链路的压力，不可能落特别多的负样本到数据流中，因此在多兴趣召回中，需要研究仅有负例数量较少时的模型性能问题，即研究一个更加稳定的负例采样策略。
将不同多兴趣召回策略的路由矩阵进行可视化，作者发现ComiRec模型很容易收敛到一个尖峰分布的崩溃解，即对于某个兴趣head而言，路由权重总是集中在某一个item上，这使得行为序列中的其他item表征很难融合到这个兴趣head中。相比ComiRec，作者提出的优化策略得到的路由权重分布则更informative。
注：作者提出的这个策略基本参考的就是Contrastive Learning with Hard Negative Samples
考虑到多兴趣召回这种select-interest-focused的训练方式会使现有难负例采样策略失效的问题，作者提出了进一步地的优化。作者认为，一个理想的难负例采样策略应该是采样那些容易被特定兴趣head错误分类的样本，同时负例的难度应该是可以被调节的，以适应不同的数据分布。借鉴对比学习的思想，作者提出了一个更好的难负例分布： 说白了就是采那些和兴趣表征相似度大的真实负例。$\beta>0$就是调节负例难度的因子。loss就被重写成如下形式，问题也变成，怎么去更好地估计出这个负例分布。 为此，作者使用了蒙特卡洛重要性采样的技术：
看起来公式比较复杂，实际上从伪代码上看，就是用u侧表征和负例表征内积来对负例加权，与u侧表征相似度越高，在分母项中该负例的权重越大，越需要被优化。
这里主要是去解决之前说的路由崩塌问题，即作者观察到，经过多轮训练后，兴趣倾向于过度关注行为序列中的单个物品。在这种情况下，只有用户历史数据中的一小部分物品被考虑到，导致多兴趣表征的表达力受损。
这种现象的原因在于item-to-interest的兴趣路由矩阵的稀疏性，说白了就是优化到最后，某个兴趣head而言，路由权重总是集中在某一个item上。这种尖峰分布下，路由矩阵的方差会比较高。因此，作者搞了一个正则化策略，去约束路由矩阵的方差，这里用方差矩阵的Frobenius范数作为度量：
其中，$C$就是矩阵的协方差，$\overline{A}$就是路由矩阵的均值。
所以总的loss function为：
作者在ComiRec-SA版本上应用了上述优化方案。这里浅浅看看效果，还是很惊艳的，把多兴趣召回的经典方案的指标刷到了新的高度。这里的UMI_HN也是应用了UMI原文中提出的难负例策略的基线。
作者同样在现有的一些sota方案上应用了上述优化点，可以看到都能不同程度提高现有方案的效果。
路由矩阵的可视化图也能显示其缓解路由崩塌的效果：
从单个策略消融看，正则化策略提升的作用更大：
其他详细的分析可以看看原文，这里就不写了。
多兴趣表征学习一个难点是怎么让不同兴趣表征尽量差异化，使得多路召回的时候尽可能overlap小，从而带来更大的增量。这篇文章用了一种正则化手段去处理，前提假设就是路由矩阵的尖峰分布问题。此外，作者也从select-interest-focused出发涉及了一种简单的难负例采样策略，动机上也非常make sense。
RecSys'23 | 港科大：重新思考推荐系统中的多兴趣召回
太长不看
港科大团队在Recsys23上提出了针对推荐系统中多兴趣召回问题的新策略。为应对select-interest-focused特性使现有负例采样策略失效和现有兴趣路由设计容易出现崩塌的挑战，作者提出难负例采样策略和路由正则化策略。这所带来的优化结果在实验证明了这些策略能有效提高推荐系统的性能，为推荐系统提供了新的优化视角。
多兴趣召回的基本框架
多兴趣召回的核心是通过用户历史行为捕捉用户的多种兴趣表示，使用不同的兴趣表示进行多路兴趣感知的差异化并行召回。
从模型结构看，多兴趣召回需要结合用户画像特征和历史行为序列特征来生成item-to-interest的兴趣路由矩阵$A\in\mathbb{R}^{n\times K}$，其中$n$是历史行为序列的长度，$K$是用户兴趣head的数量。利用兴趣路由矩阵可以将item表示映射到具体的兴趣表示$V_u\in \mathbb{R}^{d \times K}$中，即$V_u=HA $，其中$H\in\mathbb{R}^{d \times n}$是用户历史行为序列中$n$个item的特征表示。这一部分的核心主要是怎么去学习一个好的兴趣路由矩阵。
从训练策略看，对于(user, target item)一对训练正样本，将多个兴趣表示与target item的兴趣表示计算相似度后，可以采用$\mathrm{argmax}$策略，得到与target item最相似的兴趣head表示作为user侧的表征$v_u\in\mathbb{R}^{d\times 1}$，即$k=\mathrm{argmax}{(V_u^Te^{i^+})}, v_u=V_u[:,k]$。随后，采用常规的交叉熵损失函数去优化：拉近user表征和target item之间的距离，同时排开负样本item，如下图所示。核心还是怎么去做负例的采样。
一般来说，采样有两种，全库均匀采样或者batch内采样。对于batch内采负例会面临着打压高热物料的问题，所以会有一个logQ消偏的方式。
至于serving策略，则是将$K$个兴趣表征分别作为user表征进行$K$路并行召回topN个item。
多兴趣召回的两大挑战
负例采样策略
兴趣路由崩塌
优化点一：难负例采样策略
考虑到多兴趣召回这种select-interest-focused的训练方式会使现有难负例采样策略失效的问题，作者提出了进一步地的优化。作者认为，一个理想的难负例采样策略应该是采样那些容易被特定兴趣head错误分类的样本，同时负例的难度应该是可以被调节的，以适应不同的数据分布。借鉴对比学习的思想，作者提出了一个更好的难负例分布：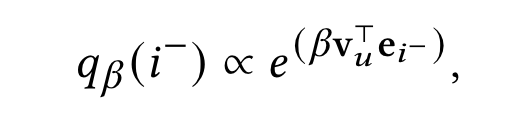
说白了就是采那些和兴趣表征相似度大的真实负例。$\beta>0$就是调节负例难度的因子。loss就被重写成如下形式，问题也变成，怎么去更好地估计出这个负例分布。
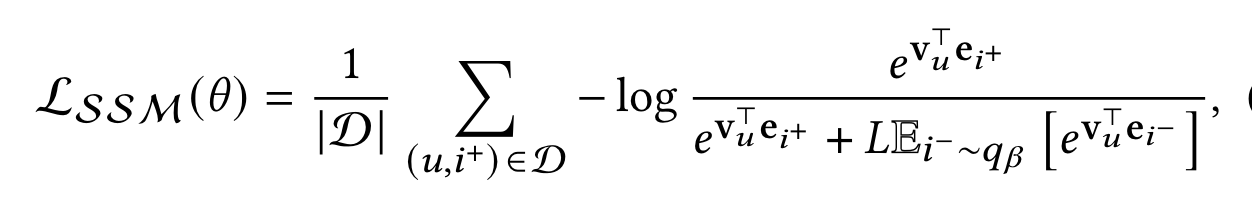为此，作者使用了蒙特卡洛重要性采样的技术：
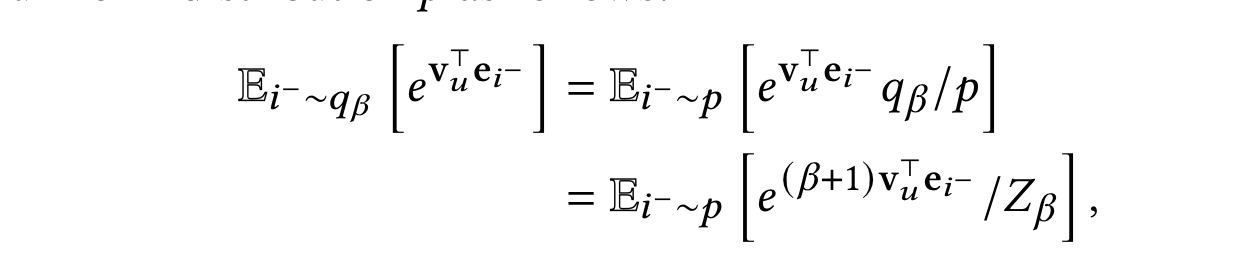
看起来公式比较复杂，实际上从伪代码上看，就是用u侧表征和负例表征内积来对负例加权，与u侧表征相似度越高，在分母项中该负例的权重越大，越需要被优化。
优化点二：路由正则化策略
这里主要是去解决之前说的路由崩塌问题，即作者观察到，经过多轮训练后，兴趣倾向于过度关注行为序列中的单个物品。在这种情况下，只有用户历史数据中的一小部分物品被考虑到，导致多兴趣表征的表达力受损。
这种现象的原因在于item-to-interest的兴趣路由矩阵的稀疏性，说白了就是优化到最后，某个兴趣head而言，路由权重总是集中在某一个item上。这种尖峰分布下，路由矩阵的方差会比较高。因此，作者搞了一个正则化策略，去约束路由矩阵的方差，这里用方差矩阵的Frobenius范数作为度量：
其中，$C$就是矩阵的协方差，$\overline{A}$就是路由矩阵的均值。
所以总的loss function为：
效果
作者在ComiRec-SA版本上应用了上述优化方案。这里浅浅看看效果，还是很惊艳的，把多兴趣召回的经典方案的指标刷到了新的高度。这里的UMI_HN也是应用了UMI原文中提出的难负例策略的基线。
作者同样在现有的一些sota方案上应用了上述优化点，可以看到都能不同程度提高现有方案的效果。
路由矩阵的可视化图也能显示其缓解路由崩塌的效果：
从单个策略消融看，正则化策略提升的作用更大：
其他详细的分析可以看看原文，这里就不写了。
写在最后
多兴趣表征学习一个难点是怎么让不同兴趣表征尽量差异化，使得多路召回的时候尽可能overlap小，从而带来更大的增量。这篇文章用了一种正则化手段去处理，前提假设就是路由矩阵的尖峰分布问题。此外，作者也从select-interest-focused出发涉及了一种简单的难负例采样策略，动机上也非常make sense。