full model:
model = pm.Model()
with model:
#cluster-wide fundamentals
Age_mu = pm.Deterministic('mean_age',pm.Beta('age_beta',2,2)*2+3)
feh_mu = pm.Deterministic('mean_feh',pm.Beta('feh_beta',2,2)*0.3-0.15)
Y_mu = pm.Deterministic('mean_Y',pm.Beta('Y_beta',2,2)*0.0334+0.2466)#0.24668 \pm 0.00007 is big bang nucleosynthesis fraction from Plank mission
MLT_mu = pm.Deterministic('mean_MLT',pm.Beta('MLT_beta',10,10)*0.6+1.7)
#per star fundamentals
M = pm.Deterministic('mass', pm.Beta('mass_beta',1.1,1.1,shape=N)*(1.2-0.8)+0.8)
Age = pm.Deterministic('age',T.ones(N)*Age_mu)
feh = pm.Deterministic('feh',T.ones(N)*feh_mu)
Y = pm.Deterministic('Y',T.ones(N)*Y_mu)
MLT = pm.Deterministic('MLT',T.ones(N)*MLT_mu)
#NN calculation
obs = pm.Deterministic('obs',m1.manualPredict(T.log10([M, Age, 10**feh, Y, MLT])))
#intermediate observables
radius = pm.Deterministic('radius', 10**obs[0])
Teff = pm.Deterministic('Teff', (10**obs[1])*5000)
L = pm.Deterministic('L', (radius**2)*((Teff/Teff_sun)**4))
logg = pm.Deterministic('logg', T.log10(100*constants.G.value*(M/radius**2)*(constants.M_sun.value/constants.R_sun.value**2)))
true_s_feh = pm.Deterministic('true_s_feh', obs[3])
obs_s_feh = pm.Normal('obs_s_feh', true_s_feh, M67['[Fe/H]_err'], observed=M67['[Fe/H]'])
#extinction prior
A_V_mu = pm.Deterministic('mean_A_V', pm.Beta('Av_beta',10,10)*0.2) # X & Y are 'sensible' values
A_V_std = pm.Lognormal('spread_A_V', T.log(0.01), 0.1) # Different X & Y but still sensible
A_V_ = pm.Normal('A_V_', 0, 1, shape=N) # an N(0, 1) dist to be scaled
A_V = pm.Deterministic('A_V', A_V_ * A_V_std + A_V_mu)
#second NN calculation
BCs = pm.Deterministic('BCs', t1.manualPredict(T.as_tensor_variable([T.log10(Teff), logg, feh, A_V])))
#BCs
BCg = pm.Deterministic('BCg', BCs[5,:])
BCbp = pm.Deterministic('BCbp', BCs[7,:])
BCrp = pm.Deterministic('BCrp', BCs[8,:])
#distance and parallax
dist_mod_ = pm.Normal('dist_mod', dist_mod, 1.0)
true_parallax = pm.Deterministic('true_parallax', 10**(-dist_mod_/5-1)*1000)
zero_pt = pm.Normal('zero_pt', M67_zero_point[0]/1000, M67_zero_point[1]/1000)
obs_parallax = pm.Normal('obs_parallax', true_parallax+zero_pt, M67_parallax[1], observed=M67_parallax[0])
#true observables
true_mG = pm.Deterministic('true_mG', -2.5*T.log10(L)+Mbol-BCg+dist_mod_)
true_Bp_Rp = pm.Deterministic('true_Bp_Rp', BCrp - BCbp)
#dealing with multiples
q = pm.Beta('q', 1.1,1.1, testval=0.8)
delta_mG = pm.Lognormal('delta_mG', T.log(0.3), 0.4)
f = pm.Lognormal('f', T.log(10),0.7)
sigma_multiple = pm.Lognormal('sigma_multiple', T.log(0.3), 0.3)
dist_singular = pm.Normal.dist(0, np.mean(M67['g_mag_err'])*f)
dist_multiple = pm.Normal.dist(-delta_mG, sigma_multiple)
#obs observables
obs_mG = pm.Mixture('obs_mG', w=[q, 1-q], comp_dists = [dist_singular, dist_multiple], \
observed=M67['g_mag'].values - true_mG)
obs_Bp_Rp = pm.Normal('obs_Bp_Rp', mu=true_Bp_Rp, sigma=M67['Bp_Rp_err'], observed=M67['Bp_Rp']) Compared to with centralized priors:
Compared to with centralized priors:
 Both results are ran with the less aggressive Av priors, and 5000 tuning steps + 1000 sampling steps.
Notably, the Rhats of the fundamentals, dist_mod and zero_pt all have lowered Rhats, while the other parameters have increased Rhats for some reason.
Both results are ran with the less aggressive Av priors, and 5000 tuning steps + 1000 sampling steps.
Notably, the Rhats of the fundamentals, dist_mod and zero_pt all have lowered Rhats, while the other parameters have increased Rhats for some reason.
 Looking at the posterior traces, it seems the higher Rhats in the parameters mean Av and below are largely contributed by one single chain that deviated from the other 3. I am not sure if this result suggests an improvement in convergence thanks to centralized priors.
Looking at the posterior traces, it seems the higher Rhats in the parameters mean Av and below are largely contributed by one single chain that deviated from the other 3. I am not sure if this result suggests an improvement in convergence thanks to centralized priors.

 The large number of tuning steps pushed most of the Rhats down, except for again the dist_mod, zero_pt pair, but also feh, Y and spread_Av.
Everything else looks sensible, including the estimated values for Y, feh, dist_mod, zero_pt, mean_Av and q (maybe not as much with the low age estimate but thats not the first time). Interestingly, the high Rhats do not destroy the corner plot:
The large number of tuning steps pushed most of the Rhats down, except for again the dist_mod, zero_pt pair, but also feh, Y and spread_Av.
Everything else looks sensible, including the estimated values for Y, feh, dist_mod, zero_pt, mean_Av and q (maybe not as much with the low age estimate but thats not the first time). Interestingly, the high Rhats do not destroy the corner plot:
 Strong covariance exist between:
dist_mod and zero_pt (they vary directly with each other in the model)
mean Av and MLT
feh and [dist_mod and zero_pt]
sigma Av vs mG_err_multiple (the larger the Av spread is, the smaller the width of the primary distribution in the mixture model has to be, to account for the width of the MS)
And also a couple other weaker covariances, which some makes sense due to definition of the model.
Strong covariance exist between:
dist_mod and zero_pt (they vary directly with each other in the model)
mean Av and MLT
feh and [dist_mod and zero_pt]
sigma Av vs mG_err_multiple (the larger the Av spread is, the smaller the width of the primary distribution in the mixture model has to be, to account for the width of the MS)
And also a couple other weaker covariances, which some makes sense due to definition of the model.
@grd349 The problem: The M67 HBM model has successfully make the sampler converge in (basically) all of the other cluster-wide parameters. The remaining two parameters that are still high in Rhat are distance modulus and Gaia parallax zero point offset. Even at 20000 tuning steps and 1000 sampling steps, they have 1.16 and 1.17 Rhats: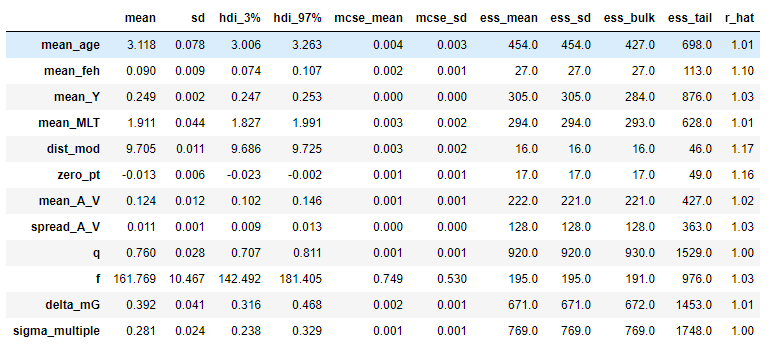
And high autocorrelation functions:
The current model:
(full model available in the next message)
Corner plot to show correlations: