for more round than r, for example draw 4 tiles to get (4s,5s) in (3*4s,2*5s,otherwise*70) invisible, we could:
- merge anything except (4s,5s) as otherwise condition to get a new
p. - enumerate all conditions: 1*4s-1*5s 1*4s-2*5s 2*4s-1*5s 2*4s-2*5s 3*4s-1*5s
- sum up all to get possibility of (4s,5s) term.
Since P(1s,2s) is dependent to P(3s,4s) while r>2, Inclusion–exclusion Principle should be used to calculate precise probability.
but the time complicity increased to O(2^n), which is not acceptable since n could up to 100.A cleaner division or some simplified method should be applyed to allow computation.
MultiNomial equally estimation can also be adjusted by analysis other's player hand based on discarded tiles.
Since here we could get all possible combination for win:
https://github.com/Ledenel/auto-white-reimu/blob/90f002077fcf0137ca66b45d80b77fb884450606/mahjong/container/pattern/reasoning.py#L169
assume each invisible tile is equal probability, we could leverage multinomial distribution for given a possible combination with r tiles in the invisible set: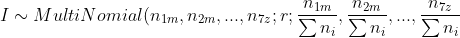)
like wikipedia explained, we could directly get all possible combinition probability just simply sum the pmf of each combination here.
here.