Segment Tree & Fenwick Tree

알고리듬 중 제가 정말 싫어하면서도 정말 좋아하기도 하는 세그먼트 트리입니다.

세그먼트 트리 관련된 문제를 풀 때, 고민되는 것 중 하나는 세그먼트 트리의 구조와 구현입니다. 오늘은 개념보다는 세그먼트 트리의 두 가지 구조와 구현들을 살펴보려고 합니다.

세그먼트 트리의 구현은 크게 세 부분으로 나뉘어집니다.

전체 구조 : 범위의 정보를 저장할 수 있는 구조를 설계합니다.

value update : 특정 범위, 또는 특정 지점의 값을 업데이트합니다.

get value : 특정 범위, 또는 특정 지점의 정보를 return 합니다.

1. General segment Tree

아래 그림과 같은 구조로 segment tree 의 element 를 저장합니다.

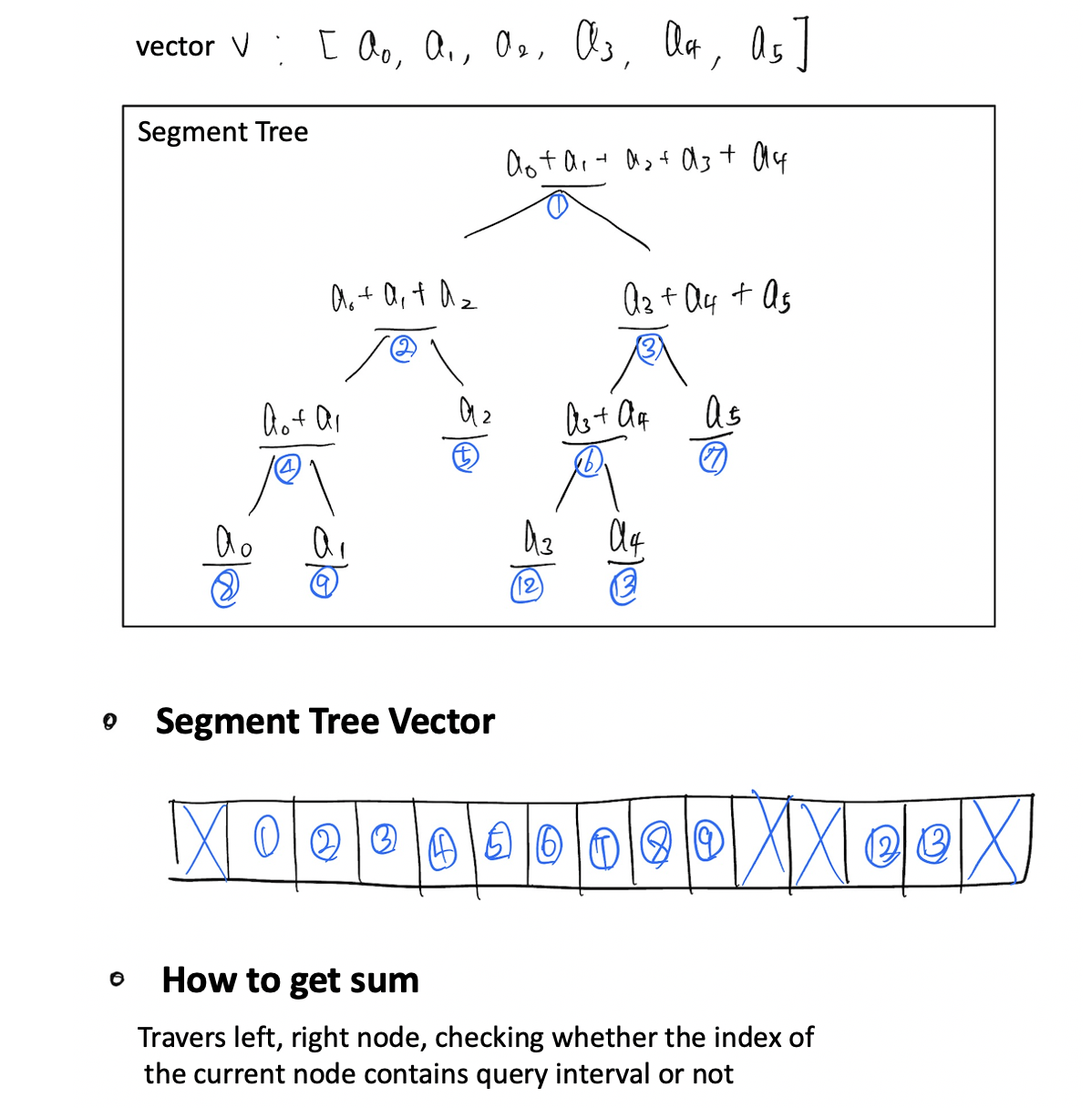
기본적인 구간합을 저장하는 segment Tree 의 구현은 아래와 같습니다.

struct segmentTree {
    vector<int> tree;
    int N;
    int length;

    segmentTree(vector<int> &v) {
        N = v.size();
        length = 4*N;
        tree.resize(length, 0);
        build(v, 1, 0, N-1);
    }

    void build(vector<int>& v, int x, int left, int right) {
        if (left == right) {
            tree[x] = v[left];
            return;
        }
        int mid = (left+right) / 2;
        build(v, 2*x, left, mid);
        build(v, 2*x+1, mid+1, right);
        tree[x] = tree[2*x] + tree[2*x+1];
        return;
    }

    void update(int x, int left, int right, int index, int value) {
        if (left == right) {
            tree[x] += value;
            return;
        }
        int mid = (left+right)/2;
        update(2*x+1, mid+1, right, index, value);
        update(2*x, left, mid, index, value);
        tree[x] = tree[2*x] + tree[2*x+1];
        return;
    }

    int getSum(int x, int left, int right, int query_l, int query_r) {
        if (right < query_l || left > query_r) {
            return 0;
        }
        if (query_l <= left && right <= query_r) {
            return tree[x];
        }
        int mid = (left+right)/2;
        int left = getSum(2*x, left, mid, query_l, query_r);
        int right = getSum(2*x+1, mid+1, right, query_l, query_r);
        return left + right;
    }
}

구체적인 구현은 풀어야하는 문제, 만들어야하는 tree에 따라 달라지겠지만,

각 레벨의 node 가 앞에서 부터 0~N 까지의 값을 저장함.

현재 node 의 범위를 절반으로 나누어 하위 level 의 left, right node 에 저장하는 방식.

으로 구현됩니다.

장점

비교적 직관적인 segment Tree 구현방식입니다. 당연히 구현하기도, 적용하기도 디버깅하기도 쉽습니다
단점
후술한 모델에 비해 느립니다. ($O(logN)$)
후술한 모델에 비해 메모리 사용이 비효율적입니다.

2. Optimized segment Tree

아래 그림과 같은 구조로 segment tree 의 element 를 저장합니다.

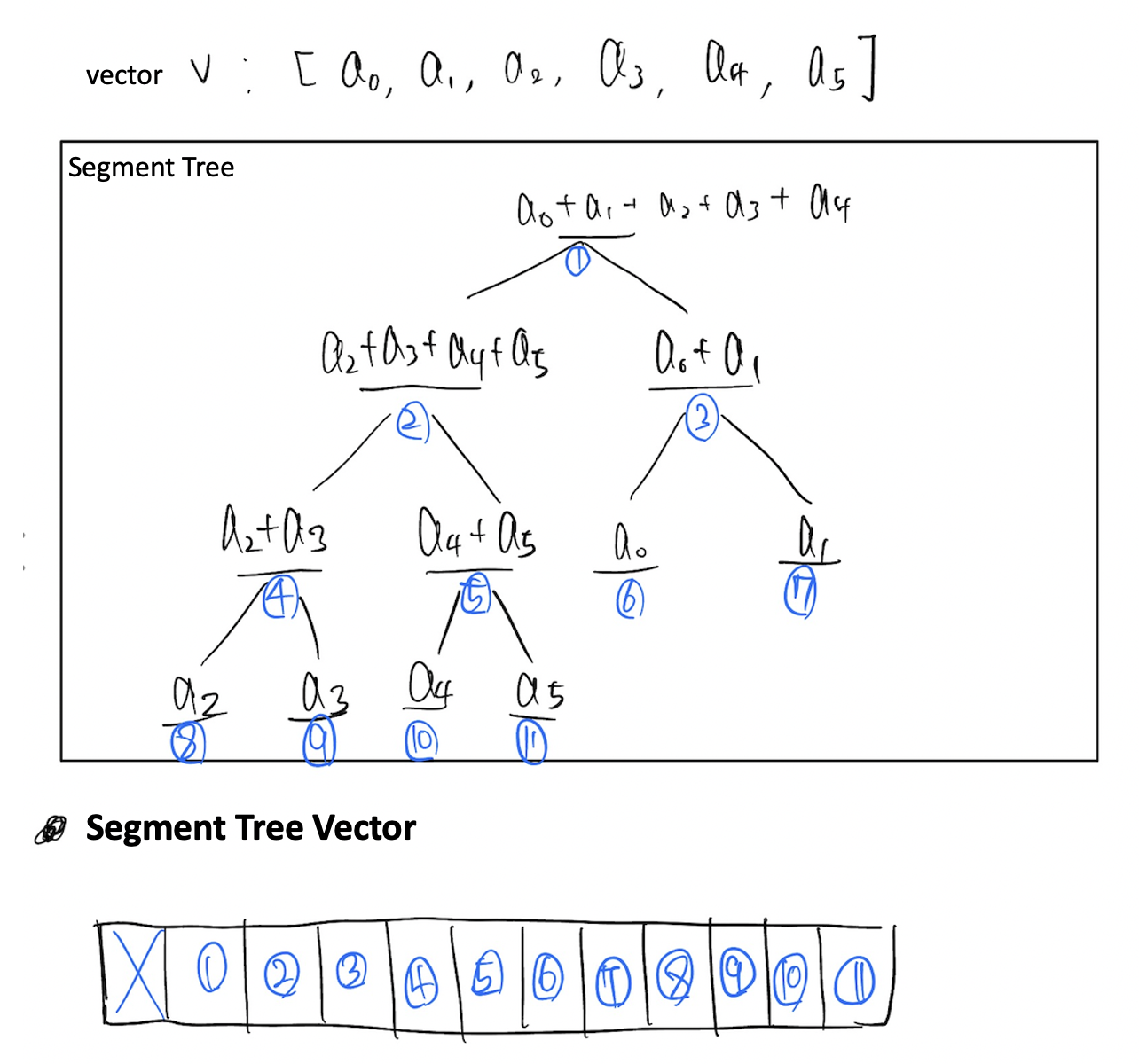
기본적인 구간합을 저장하는 segment Tree 의 구현은 아래와 같습니다.

struct segmentTree {
    vector<int> tree;
    int N;
    int length;

    segmentTree(vector<int> &v) {
        N = v.size();
        length = 2*N;
        tree.resize(length, 0);
        build(v);
    }

    void build(vector,int>& v) {
        for (int i=0; i<N; i++) {
            tree[i+N] = v[i];
        }
        for (int i=N-1; i>=0; i--) {
            tree[i] = tree[i*2] + tree[i*2+1];
        }
    }

    void update(int index, int value) {
        index += N;
        tree[index] += value;
        while (index>1) {
            index /= 2;
            tree[index] = tree[index*2] + tree[index*2+1];
        }
    }

    int query(int left, int right) {
        int result = 0;
        left += N;
        right += N;
        while (left < right) {
            if (left%2 == 1) {
                // left의 index가 홀수이면 상위 노드 구간 포함 안됨.
                result += tree[left];
                left++;
            }
            left /= 2;
            if (right%2 == 0) {
                // right의 index가 짝수이면 상위 노드 구간 포함 안됨.
                result += tree[right];
                right--;
            }
            right /= 2;
        }
        if (left == right) {
            result += tree[left];
        }
        return result;
    }
}

구체적인 구현은 풀어야하는 문제, 만들어야하는 tree에 따라 달라지겠지만,

segment tree 에서 특정 index 의 접근이 index+N 으로 이루어짐. 1-1. query 또는 범위에 대한 접근이 O(1) 으로 효율적으로 이루어짐

segment tree 의 같은 level 내에서의 범위가 순차적으로 이루어져 있지 않음.

으로 구현됩니다.

장점

element 에 대한 접근이 O(1) 으로 이루어질 수 있고 general segment tree에 비해 구간합을 구하는 속도가 비교적 빠릅니다. (최악의 경우 $O(logN)$)
또한 query 에 대한 접근이 index 로 바로 이루어질 수 있으므로 현재 node 의 범위를 저장할 필요없이 처리 가능합니다.
단점
구현이 직관적이지 않고, 따라서 문제에 적용하기 어렵습니다.
디버깅 역시 같은 이유로 어렵습니다.

3. Fanwick Tree (binary index tree)

segment Tree 의 일종은 아니고.. 구간합과 같은 문제를 풀 때 사용되는 기법 주 하나입니다. 다만 조금 더 한정된 경우에만 사용 가능합니다. segment Tree 와 마찬가지로 개념에 대한 설명은 잘 되어 있는 경우가 많아서 제외하겠습니다. ...사실 segment Tree 글에 안 쓰려고했는데 쓰다보니 허전해서 작성했씁니다.

struct fanwickTree {
    vector<int> tree;
    int N;

    fanwickTree(vector<int> &v) {
        N = v.size();
        tree.resize(N+1, 0);
        for (int i=0; i<N; i++) {
            update(i+1, v[i]);
        }
    }

    void update(int index, int val) {
        while (index <= n) {
            farr[index] += val;
            index += (index & -index);
        }
    }

    int sum(int index) {
        int result = 0;
        while (index>0) {
            ans += farr[index];
            index -= (index & -index);
        }
        return result;
    }

    int query(int left, int right) {
        return sum(right+1) - sum(left);
    }
}

장점

메모리 효율적이며, 속도 역시 빠릅니다. (최악의 경우 $O(logN)$.)
단점
개념이 헷갈리며, indexing 기법이 bit 연산이라 처음 접하는 사람에게는 어렵습니다.
사용할 수 있는 경우가 제한적입니다.

Conclusion

이렇게 segment Tree 의 구현 방법 두 가지를 살펴보았습니다. structure 를 사용하지 않고도 구현할 수 있지만, 두 가지 구현 방법을 철학을 가장 쉽게 이해할 수 있는 구조라고 생각해서 structure 를 사용했습니다.

LogicBaron / StoneAlgorithm