Graph Rewriting

[jeannieyeliu]

https://en.wikipedia.org/wiki/Graph_rewriting

[jeannieyeliu]

Graph rewriting

the technique of creating a new graph out of an. original graph algorithmically.

basic idea

• state of a computation → graph
• steps in that computation → transformation rules on that graph.

structure

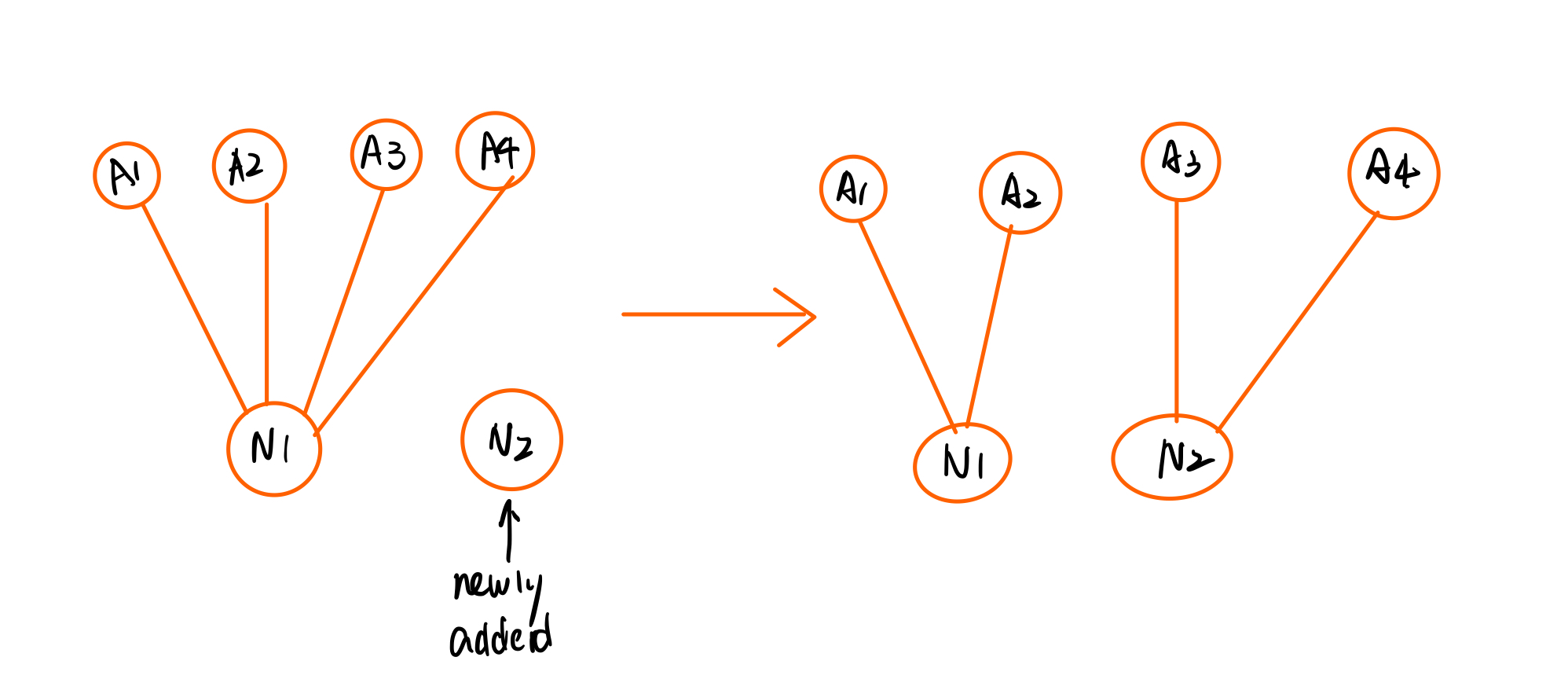
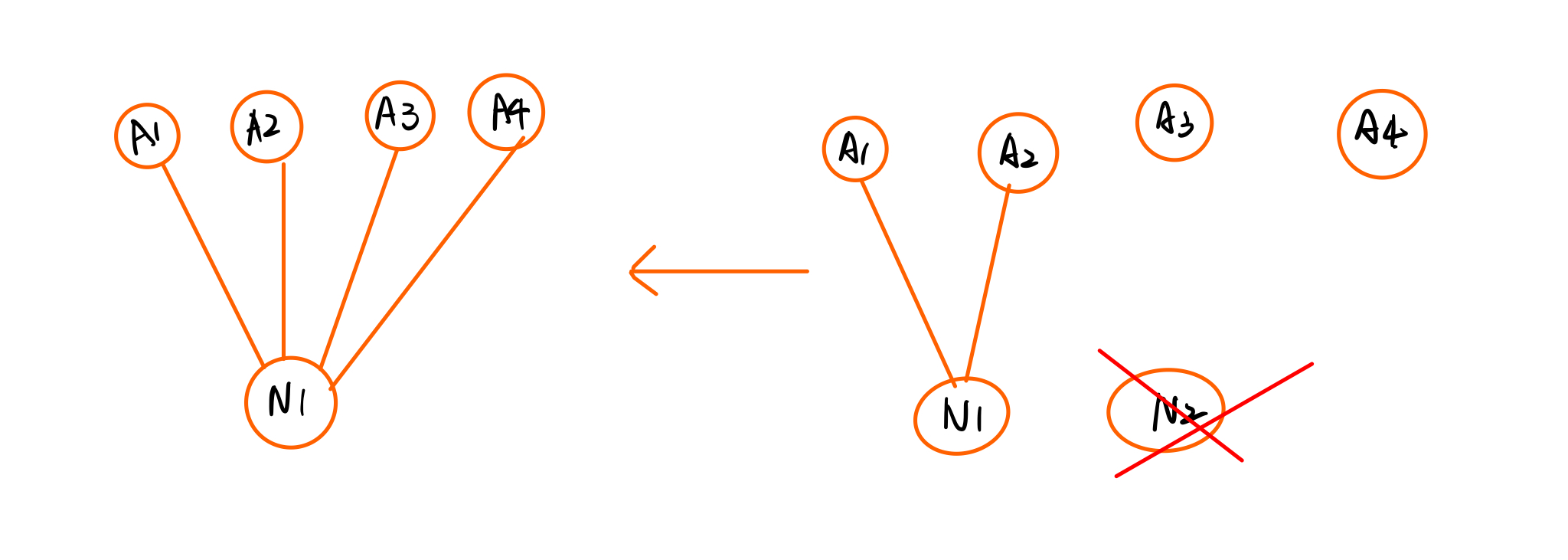
• a transformation rule consist of :
  • original graph, which is to be matched to a
  • subgraph in the complete state,
  • replacing graph, which will replace the matched subgraph.
  • represented as : L→R

    L is called pattern graph (or left-hand side)
    R is called replacement graph (or right-hand side)

how to apply the rule to the host graph:

1. searching for an occurrence of the pattern graph L. (pattern matching )
2. replace the found occurrences with the replacement graph R.

[jeannieyeliu]

Graph rewirting approaches

Algebraic approach

• [x] double-pushout (DPO)

• [x] Single-pushout (SPO), (in consrast to DPO)

• [ ] Determinate graph rewriting

• [ ] Term graph rewriting

[CMCDragonkai]

It's important that we figure out how to use this for configuration changes and dealing with atomicity and action at a distance problems. Please look these up @imliuye and I will expand on this examples later.

[jeannieyeliu]

Double pushout graph rewriting

DPO Graph rewriting allows the specification of graph transformations by specifying a pattern of fixed size and composition to be found and replaced, where part of the pattern can be preserved.

structure

• a finite graph as the start state
• a set of finite/countable graphs as derivations rules that are:
  • labeled spans in the category
  • composed of monomorphism
  • can be non-deterministic: (several distinct matches can be possible), e.g. r = (L ← K → R）where K → L is injective. K is called gluing graph/ invariant.

two steps for rewritting

• deletion:

  After a match from the left hand side to  G is fixed, 
  nodes and edges that are not in the right hand side are deleted. 
  The right hand side is then glued in.
  Gluing graphs is in fact a pushout construction in the category of graphs, 
  and the deletion is the  same as finding a pushout complement, hence the name.

• addition

  A rewriting step or application of a rule r to a host graph G is defined by two pushout diagrams both originating in the same morphism k: K -> D , where D is a context graph (this is where the name double-pushout comes from). Another graph morphism m: L-> G models an occurrence of L in G and is called a match. Practical understanding of this is that L is a subgraph that is matched from G , and after a match is found, L is replaced with R in host graph G where K serves as an interface, containing the nodes and edges which are preserved when applying the rule. The graph K is needed to attach the pattern being matched to its context: if it is empty, the match can only designate a whole connected component of the graph G.

[jeannieyeliu]

Single pushout graph rewriting

in contrast a graph rewriting rule of the SPO approach is a single morphism in the category of labeled multigraphs and partial mappings that preserve the multigraph structure: r: L -> R. Thus a rewriting step is defined by a single pushout diagram. Practical understanding of this is similar to the DPO approach. The difference is, that there is no interface between the host graph G and the graph G' being the result of the rewriting step.

From the practical perspective, the key distinction between DPO and SPO is how they deal with the deletion of nodes with adjacent edges, in particular, how they avoid that such deletions may leave behind "dangling edges". The DPO approach only deletes a node when the rule specifies the deletion of all adjacent edges as well (this dangling condition can be checked for a given match), whereas the SPO approach simply disposes the adjacent edges, without requiring an explicit specification.

There is also another algebraic-like approach to graph rewriting, based mainly on Boolean algebra and an algebra of matrices, called matrix graph grammars

[jeannieyeliu]

Determinate graph rewriting

Yet another approach to graph rewriting, known as determinate graph rewriting, came out of logic and database theory. In this approach, graphs are treated as database instances, and rewriting operations as a mechanism for defining queries and views; therefore, all rewriting is required to yield unique results (up to isomorphism), and this is achieved by applying any rewriting rule concurrently throughout the graph, wherever it applies, in such a way that the result is indeed uniquely defined.

[jeannieyeliu]

Term graph rewriting

involves the processing or transformation of term graphs (also known as abstract semantic graphs) by a set of syntactic rewrite rules.

Term graphs are a prominent topic in programming language research since term graph rewriting rules are capable of formally expressing a compiler's operational semantics. Term graphs are also used as abstract machines capable of modelling chemical and biological computations as well as graphical calculi such as concurrency models. Term graphs can perform automated verification and logical programming since they are well-suited to representing quantified statements in first order logic. Symbolic programming software is another application for term graphs, which are capable of representing and performing computation with abstract algebraic structures such as groups, fields and rings.

The TERMGRAPH conference focuses entirely on research into term graph rewriting and its applications.

[jeannieyeliu]

This idea might somehow related to #issue 54 consider the following situation: The change of constraints when new resources are available,

in the following example, when a new Hardware N2 is added, constraints should be redefined and automatons A1, A2, A3, A4 should be reallocated. resources reallocation could be somehow changed by a graph rewriting system

And vice versa, when N2 is down, resource should be reallocated

[jeannieyeliu]

Now we need to figure out what rules should be defined in the graph rewritting system

[jeannieyeliu]

Another idea is to translate abstract description into more concrete representations. In the emergence system for instance: