Convergence issue for oblique level-set lattices (subpixel averaging?)

[thchr]

Hi @stevengj,

I've hit what I think is a surprising performance degradation in a rather particular setting, and I'm wondering if it could be considered a genuine issue. Right off the bat: I'm sorry that the description below is so verbose.

The problem manifests as extremely slow/non-existent convergence (resolution-wise) in an (unphysical) symmetry-breaking of computed frequency spectra.

Specifically, for a (3D) calculation that involves the following three elements:

1. ... material properties specified via material-func (i.e. a level set surface),
2. ~... with associated anisotropic material response (i.e. nonzero epsilon-offdiag),~
3. ... in a non-rectangular lattice,

I observe that frequencies ω(k) and ω(k′) with k and k′ related by a symmetry of the lattice differ (although, physically, ω(k) = ω(k′)). This is of course not terribly surprising due to discretization etc., but I find that |ω(k) - ω(k′)| converges far slower/not at all in the above setting. If either of these three elements are removed, good convergence is restored. [edit: actually, turns out changing point 2 doesn't do anything] The issue is best illustrated by examples: several included below.

I'm guessing this is related to the subpixel averaging step in src/maxwell/maxwell_eps.c, more specifically around here, but I'm not entirely sure. I'd be interested in working to fix this, if you think it is a fixable problem (and especially if I could get some pointers on where to investigate further).

Minimal examples demonstrating the issue

Consider the following setup: an oblique lattice (the primitive lattice of a conventional tI Bravais lattice with axis lengths 1, 1, and 0.8) with a gyromagnetic sphere at its center under a B-field along the (Cartesian) z-axis. Among the symmetries of the system is a (Cartesian) y-mirror symmetry m₀₁₀ (m₁₀₁ in the lattice basis).

The following .ctl sets up a system like this (except for the sphere-part; follows next):

; ─────────────────────────── MAIN DEFAULT PARAMETERS ──────────────────────────
(define-param res     32)  ; resolution
(define-param kvecs   (list (vector3 0.234 0.45 0.321) (vector3 0.234 -0.45 0.321) )) ; list of k-vectors in a Cartesian basis (differ by sign of y-component)
(define-param rvecs   (list (vector3 -0.5 0.5 0.4) (vector3 0.5 -0.5 0.4) (vector3 0.5 0.5 -0.4) ))
(define-param has-tr  #f)  ; whether we assume B = 0 (#t) or apply a B-field along the cartesian z-direction (#f)

; ──────────────────────────── PREP-WORK ────────────────────────────
(set! resolution res)
(set! num-bands  4)
(set! output-epsilon (lambda () (print "... skipping output-epsilon\n"))) ; remove output of *.h5 unitcell files

; ──────────────────── CRYSTAL SYSTEM/DIRECT BASIS ─────────────────────
(set! geometry-lattice (make lattice
    (size 1 1 1)
    (basis1 (list-ref rvecs 0)) (basis2 (list-ref rvecs 1)) (basis3 (list-ref rvecs 2))
    (basis-size (vector3-norm (list-ref rvecs 0)) (vector3-norm (list-ref rvecs 1)) (vector3-norm (list-ref rvecs 2)))
))

; ──────────────────── K-POINTS ─────────────────────
(set! k-points (map cartesian->reciprocal kvecs))

; ──────────────────── MATERIAL ─────────────────────
(define epsin 13)
(define epsin-diag    (vector3 14.00142849854971 14.00142849854971 13.0)) ; equiv. to a normalized B field of 0.4, applied to epsin=13
(define epsin-offdiag (cvector3 0.0+5.2i 0.0+0.0i 0.0+0.0i))

(define material-inside
    (cond
        (has-tr (make dielectric (epsilon epsin)) )
        (else   (make medium-anisotropic (epsilon-diag epsin-diag) (epsilon-offdiag epsin-offdiag)) )
    )
)
(define material-outside (make dielectric (epsilon 1)))

; ──────────────────── GEOMETRY ─────────────────────
; implement a gyromagnetic sphere, either via `sphere` or `material-func`
(define rad 0.25) ; sphere radius
; include("geometry-by-sphere.scm")       ; <----------- VARIABLE BITS BELOW
; include("geometry-by-materialfunc.scm") ; <----------- VARIABLE BITS BELOW

; ───────────────────────────────── DISPERSION ─────────────────────────────────
(run-all)

make sphere approach

Now, if we create an gyromagnetic sphere using make sphere, everything works well (this is the geometry-by-sphere.scm file above):

(set! geometry (list
    (make sphere
        (center 0 0 0)
        (radius rad)
        (material material-inside)
    )
))

and we can plot the absolute difference between the frequencies at the two k-points (i.e. k and k′ = m₀₁₀k) as a function of computation resolution:

So far, so good.

make material-function approach

If we instead create the same sphere using a level set function (this is the geometry-by-materialfunc.scm file above), convergence slows down significantly:

(define rad2 (* rad rad))
(define (f r)
    (let ((rc (lattice->cartesian r)))
        (- (abs (vector3-cdot rc rc)) rad2)
    )
)

(define (level-set-material r)
    (cond 
        ((< (f r) 0.0) material-inside)
        (else material-outside)
    )
)

(set! default-material (make material-function (material-func level-set-material)))

Of course, the `make sphere` and `make material-function` approaches agree roughly about the spectra (click to see plots)

| `make sphere` | `make material-function` | | --- | --- | |  |  |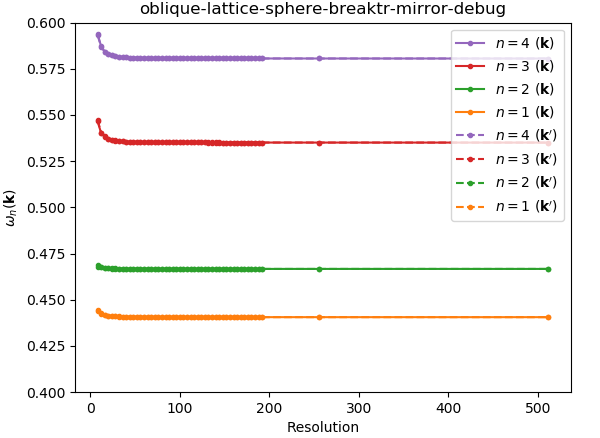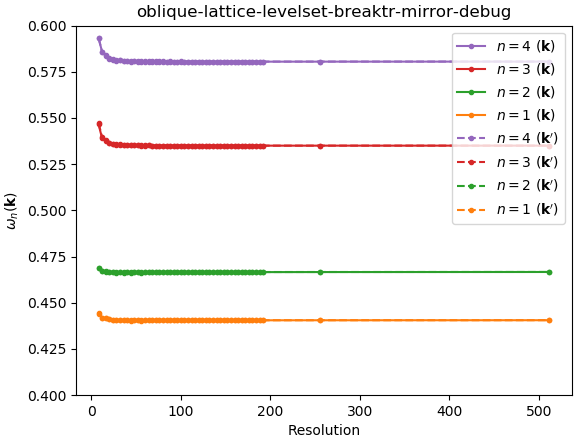

make material-function for a rectangular lattice

If we swap out the oblique lattice for a rectangular one, e.g. with rvecs equal to (vector3 1 0 0) (vector3 0 1 0) (vector3 0 0 0.8), good convergence is restored:

make material-function with more complicated geometry

Keeping the oblique lattice, but swapping out the sphere for a more complicated geometry (that retains a (Cartesian) {m₀₁₀|0,0,⅖} symmetry though) makes the problem even more evident:

Effectively, bands 2, 3, and 4 stop converging.

k-dependence of issue

Above, I just picked two random k-points; but the issue is k-point dependent - some ponits are strongly affected, and others are not. I found that the issue can be particularly strong when k is near a (symmetry-protected) nodal point at generic k. (This is my research motivation for this)

Example (click to expand)

As an example, here is a slice of the BZ for a lattice in SG 110, which should have a Cartesian *y*-symmetry, but evidently doesn't (at a resolution of 50): | Band 2 | Band 3 | | :--: | :--: | |  |  |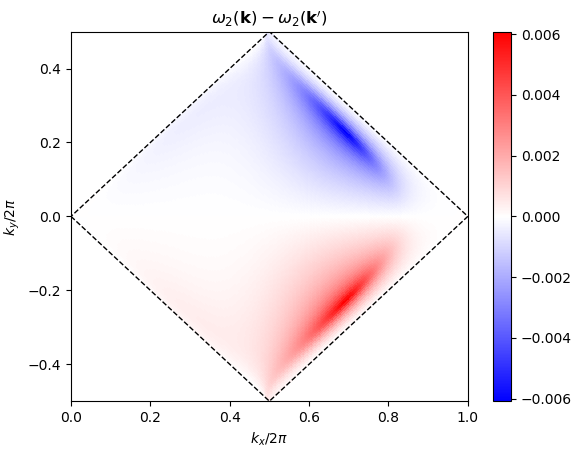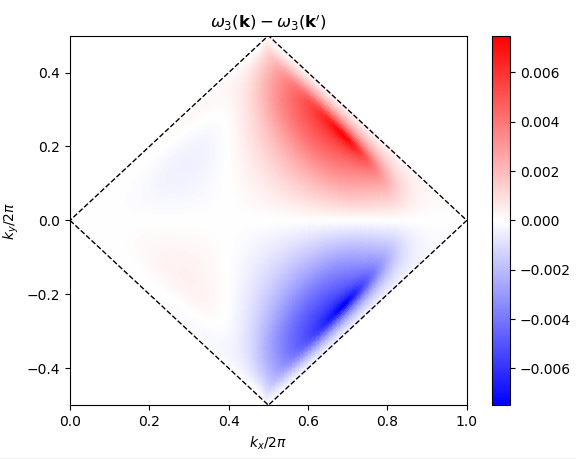

[thchr]

I had somehow missed that the anisotropic element isn't really crucial to this issue (see minor edits/strike-outs above).

As an example, running the same examples as in the make material-function section, but with a simple isotropic material (i.e. toggling has-tr to #t) instead doesn't improve convergence at all:

So, it seems the issue can be boiled down to a clash between non-rectangular basis vectors and a level set function? In that case, could it be the related to the computation of the normal vectors at interfaces?

[stevengj]

I'm not sure I see the issue in the computation of the normal vector?

(In general, it is hard to do accurate subpixel averaging for user-defined material functions, though in principle we could do better as discussed in https://github.com/NanoComp/meep/issues/1229)

[thchr]

Ah, yeah, you're probably right that the normal vector is not to blame: I checked some things last Friday about the normal vector (more below) and ended up losing faith in that explanation as well.

For the make material-function approach to creating a sphere, there's seems to be about a 7-8% mean error error in the calculation of the normal vector at "surface voxels" (checked for resolutions up to 128; doesn't seem to improve with resolution). But that error seems to be pretty much independent of whether or not the lattice is rectangular or not (so that suggests this isn't the origin of this issue, I guess?). On the other hand, 7-8% is larger than I had expected? (If I bump the NUM_QUAD variable from sphere-quad.c up to 72 from 50, the error is decreased by 1-2 percentage points)

(I checked this with the following diff)

``` --- a/src/maxwell/maxwell_eps.c +++ b/src/maxwell/maxwell_eps.c @@ -392,6 +392,8 @@ void set_maxwell_dielectric(maxwell_data *md, real moment_mesh[MAX_MOMENT_MESH][3]; real moment_mesh_weights[MAX_MOMENT_MESH]; real eps_inv_total = 0.0; + real total_normdelta = 0.0; + int N_surface_points = 0; int i, j, k; int mesh_prod; real mesh_prod_inv; @@ -440,7 +442,6 @@ void set_maxwell_dielectric(maxwell_data *md, maxwell_sym_matrix_invert(md->eps_inv + xyz_index, &eps_mean); - goto got_eps_inv; norm0 = R[0][0] * normal[0] + R[1][0] * normal[1] + R[2][0] * normal[2]; @@ -620,6 +621,31 @@ void set_maxwell_dielectric(maxwell_data *md, norm_len = sqrt(norm0*norm0 + norm1*norm1 + norm2*norm2); } + /* TESTING NORMAL VECTOR */ + if (means_different_p && norm_len > SMALL) { + real r[3], rc[3]; + real c1, c2, c3, rc_len, normdelta; + c1 = n1 <= 1 ? 0 : 0.5; /* offsets (negative) */ + c2 = n2 <= 1 ? 0 : 0.5; + c3 = n3 <= 1 ? 0 : 0.5; + + r[0] = i1 * s1 - c1; + r[1] = i2 * s2 - c2; + r[2] = i3 * s3 - c3; + rc[0] = R[0][0]*r[0] + R[1][0]*r[1] + R[2][0]*r[2]; + rc[1] = R[0][1]*r[0] + R[1][1]*r[1] + R[2][1]*r[2]; + rc[2] = R[0][2]*r[0] + R[1][2]*r[1] + R[2][2]*r[2]; + rc_len = sqrt(rc[0]*rc[0] + rc[1]*rc[1] + rc[2]*rc[2]); + + /* |̂r - ̂n| (note extra minus sign because of orientation difference...) */ + normdelta = sqrt( pow((-rc[0]/rc_len) - (norm0/norm_len), 2) + + pow((-rc[1]/rc_len) - (norm1/norm_len), 2) + + pow((-rc[2]/rc_len) - (norm2/norm_len), 2) ); + + total_normdelta += normdelta; + N_surface_points += 1; + } + if (means_different_p && norm_len > SMALL) { real x0, x1, x2; @@ -722,6 +748,8 @@ void set_maxwell_dielectric(maxwell_data *md, md->eps_inv[xyz_index].m22); }}} /* end of loop body */ + printf("\n\n------\naverage |r-n| = %.4f\n------\n\n", total_normdelta / N_surface_points); + mpi_allreduce_1(&eps_inv_total, real, SCALAR_MPI_TYPE, MPI_SUM, mpb_comm); n1 = md->fft_output_size; ```

I guess the thing that confuses me here is why everything works quite well for rectangular lattices (in the sense that |ω(k) - ω(k′)| converges quite fast), even when using a level set function, but then doesn't work well at all for non-rectangular lattices? Any thoughts on this? If the normal vector is not the problem, what could be?

The proposal from https://github.com/NanoComp/meep/issues/1229 does sound very nice and worthwhile; but I don't understand why the two specific elements above - level set and non-orthogonal lattice vectors - are particularly bad for subpixel averaging?

[thchr]

OK, having tried a bunch of stuff (increasing mesh-size, cross-checking computed means, manually overriding the approximated normal, etc.) to no avail, I finally did what I should have done initially and consulted your original Opt. Express and PRE for Kottke averaging (especially Section VI).

From my current understanding, the salient point is simply that Kottke averaging isn't implemented for material-function cases (or gridded data values), instead employing the heuristic "projector" averaging from Eq. (12) of the Opt. Express. I'm guessing the excellent convergence in the rectangular lattice actually is the outlier - corresponding to the comment from the PRE that

[...] we had observed what seemed to have been quadratic convergence from the heuristic scheme [6], but this result seems to have been fortuitous [...]

I guess your original point was that it is tricky to think about implementing Kottke averaging for a general material-function, which wouldn't necessarily be a simple two-material level set? In principle, I imagine the Kottke averaging step could still be implemented instead of the projector averaging, though, right? Although getting the local interface-oriented coordinate system right seems potentially a bit painful.

Any thoughts on whether that would be likely to improve things substantially (for level sets, with normals approximated by the currently implemented moment-approach)?

[stevengj]

In principle, I imagine the Kottke averaging step could still be implemented instead of the projector averaging, though, right?

Absolutely. Basically, you would

1. estimate the normal vector as now
2. using the normal vector, construct a rotation matrix R so that ε′=RᵀεR rotates ε into the interface coordinate frame
3. compute τ(ε′) at each point in the mesh grid (as defined in the Kottke paper, )and average τ to obtain the mean τₘ
4. compute the effective ε, given by Rτ⁻¹(τₘ)Rᵀ, where τ⁻¹ is given by equation (23) in the Kottke paper

[thchr]

OK, that (fortunately) matches up with my conception of what the todos would be: thanks for verifying that!

Do you agree that if this is implemented that it would likely improve convergence, even with the approximate normal vectors?

[stevengj]

Yes, I hope so.

[stevengj]

At least for anisotropic materials. For isotropic materials the projector method is equivalent to the Kottke method, so I wouldn't expect any difference.

[thchr]

Hmm, for isotropic materials then: why do you think the convergence rate is so much worse for the oblique lattice (i.e. the example in https://github.com/NanoComp/mpb/issues/126#issuecomment-710149318)? The isotropic case's convergence rate is pretty comparable to the anisotropic case (for oblique lattice with level set).

[stevengj]

I don't know, but it's not the projection formula per se.

Maybe there's some missing coordinate transform (between Cartesian and lattice bases) somewhere in the fallback material-averaging code?

[thchr]

I took a stab at implementing the Kottke averaging step over in https://github.com/thchr/mpb/commit/7e671b18f05b829472b86ec174de9ad38c0fb649.

Observations:

1. For the by-individual-frequencies convergence (i.e. |ω(k) - ω"true"(k)| vs. resolution):
   1. For isotropic permittivities, nothing changes relative to the projection approach (except very minor spurious deviations), consistent with your prediction.
   2. For anisotropic permittivities, convergence plots do change - but I don't see a very clear convergence improvement overall (edited: initially, I thought I saw one - with more data, that went away).
2. For the "symmetry-breaking" convergence (i.e. |ω(k) - ω(k′)| vs. resolution), nothing really changes: The convergence plots are remarkably robust and only differ very slightly between the projection and Kottke approaches (even when the overall convergence does differ a lot), regardless of isotropy/anisotropy. This is somewhat puzzling to me: I guess it could imply that the symmetry-breaking issue isn't really related to subpixel averaging at all [edit: but if not, I don't see how |ω(k) - ω(k′)| can converge for make sphere but not make material-function]? Thoughts welcome!

I can submit a PR from https://github.com/thchr/mpb/commit/7e671b18f05b829472b86ec174de9ad38c0fb649, if we can convince ourselves that the implementation is sound.

[thchr]

Maybe there's some missing coordinate transform (between Cartesian and lattice bases) somewhere in the fallback material-averaging code?

I tried to test this earlier today by printing out the values of eps_mean_inv and eps_inv_mean as computed with the make sphere and make material-function approaches (by instrumenting bits of mean_epsilon_func() and set_maxwell_dielectric(), respectively), comparing grid-point-by-grid-point for interface voxels. With sufficiently high mesh-size, they seemed to converge pretty well though, so I was inclined to rule this out.

[stevengj]

It could be that the normal vector and/or the integration just isn't accurate enough…?

[thchr]

Hmm, yeah, I had been trying to test that before implementing the Kottke step as well (improving either separately, not jointly though).

I've tested it with the Kottke implementation now as well, with the following modifications:

• Normal vector: Since this is a sphere, just compute the normal vector analytically and use that instead (see https://github.com/thchr/mpb/commit/c972eea5f2bc10c00949a1fd11b3a27af0b7063a)
• Integration: Increase the mesh_size for all the "interface voxels" to mesh_fine_size = 9 (using the original mesh_size = 3 to identify the presence of such voxels) (see https://github.com/thchr/mpb/commit/33856cbcb69fe8a734ae617b73f7a33c56f9d314).

Convergence comparison

Unfortunately, though, I don't see a lot of clear-cut benefit in terms of convergence: below are convergence plots [1][2] for the case of a gyromagnetic sphere in an oblique lattice created with make material-function:

[1] I define the "true" reference frequencies from a 512-resolution calculation with make sphere. [2] A few resolutions are missing occasionally: I got impatient.

Master

Overall convergence	Symmetry breaking convergence

Kottke (https://github.com/thchr/mpb/commit/7e671b18f05b829472b86ec174de9ad38c0fb649)

Overall convergence	Symmetry breaking convergence

Kottke w/ finer integration (https://github.com/thchr/mpb/commit/33856cbcb69fe8a734ae617b73f7a33c56f9d314) & manual normal vector (https://github.com/thchr/mpb/commit/c972eea5f2bc10c00949a1fd11b3a27af0b7063a)

Overall convergence	Symmetry breaking convergence

make sphere (master)

For make sphere, the convergence is far better (as noted in the OP) and less erattic too:	Overall convergence	Symmetry breaking convergence

I'm quite at a loss of what the issue could be here. I've checked the new Kottke implementation carefully; pretty sure that's solid. Not quite sure how to proceed from here.

[thchr]

OK, pretty sure I figured out the issue, at long last. The root cause of the lingering poor convergence performance is indeed the normal vector computation. Two sub-aspects contribute (fixing either in isolation doesn't do the trick):

1. The lack of precision in computing the normal vector n via the moment.
2. Missing identification of an interface point (due to small moments): The permittivity averaging step is guarded by a check if (means_different_p && norm_len > SMALL). While means_different_p generally seems to pick up interface points with high fidelity, the norm_len > SMALL check often returns false spuriously (i.e. even if the voxel really intersects an interface) due to too-small interface moments.

It seems to me that 2. in principle is easy to fix: just drop the norm_len > SMALL check. (Though I'm wondering if that would impact calculations with smoothly varying permittivities?)

I'm not sure about fixing 1. in generality though (which, presumably, might also fix 2. automatically). I can see that sphere_quad.c also implements a 72 point quadrature rule, but when I tested it earlier in the week it didn't seem to improve the moment calculation all that much. The mean error right now is about 7% for the sphere.

[Edit: right now, the moment averaging mesh's extent is set by MOMENT_MESH_R = 0.5, which gives a spherical mesh that lies wholly within the voxel - on the other hand, it "misses" the voxel's corners. Bumping it up to 1/sqrt(2) (i.e. including the entire voxel, as well as some of the neighboring voxels) seems to improve things quite a lot in preliminary experiments. This might be a pragmatic solution: bump NQUAD3 to 72 and MOMENT_MESH_R to 1/sqrt(2)?]

[thchr]

For the record, the issue that originally spurred me to work on this - namely the nearly complete nonconvergence of symmetry breaking in a more complicated geometry than the sphere (i.e. this graph) - actually remains essentially unaffected by the improvements in #127; I have no idea why still. This is just to say that I believe there could still be some oddities remaining for the general case.