Solution diverges for simple 2nd-order linear ODE

[shuheng-liu]

I was solving the Taylor-Couette equation, which, under mild assumptions, is simplified to this 2nd order linear ODE:

Equation Statement

The solution to the above equation should be where A and B are arbitrary constants.

Boundary Condition and Analytical Solution

Under the Dirichlet condition y(0.1) == y(10) == 10.1, the solution can be uniquely determined as: , which looks like this

.

Expected Behaviour

As the training proceeds, the net should return a solution that first goes down until x == 1 and go back up again when x > 1

Actual Behaviour

However, using the following code, the network gives a solution that keeps straying away from the analytical solution.

import torch
import numpy as np
import matplotlib.pyplot as plt
from neurodiffeq import diff
from neurodiffeq.ode import solve, Monitor, ExampleGenerator
from neurodiffeq.ode import IVP, DirichletBVP
from neurodiffeq.networks import FCNN

net = FCNN(n_input_units=1, n_output_units=1, n_hidden_units=512, n_hidden_layers=0)
x_1 = 0.1
x_2 = 10.0
ode = lambda y, x: diff(y, x, order=2) + diff(y, x) / x - (y / x ** 2)
condition = DirichletBVP(x_1, 10.1, x_2, 10.1)
monitor = Monitor(t_min=x_1, t_max=x_2, check_every=50)
train_generator = ExampleGenerator(256, t_min=x_1, t_max=x_2, method='uniform')
valid_generator = ExampleGenerator(2048, t_min=x_1, t_max=x_2, method='equally-spaced')
monitor.check_every = 50

# solve the ODE
solution, loss, internals = solve(
    ode=ode,
    condition=condition, 
    t_min=x_1, 
    t_max=x_2, 
    monitor=monitor, 
    max_epochs=5000,
    return_internal=True,
    train_generator=train_generator,
    valid_generator=valid_generator,
    batch_size=train_generator.size,
)

Here is a gif file that shows how the model is performing. Note that not only does the network give a solution that looks drastically different from the analytic one, but also the solution is being scaled in the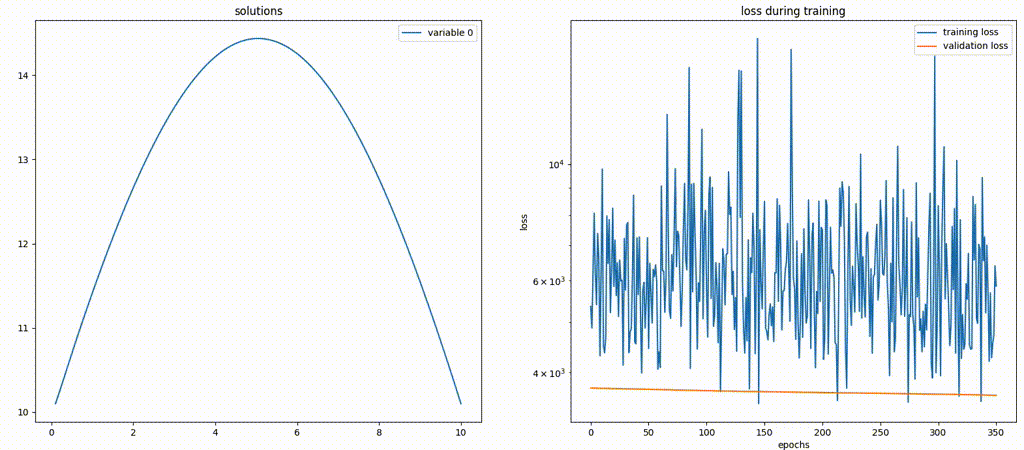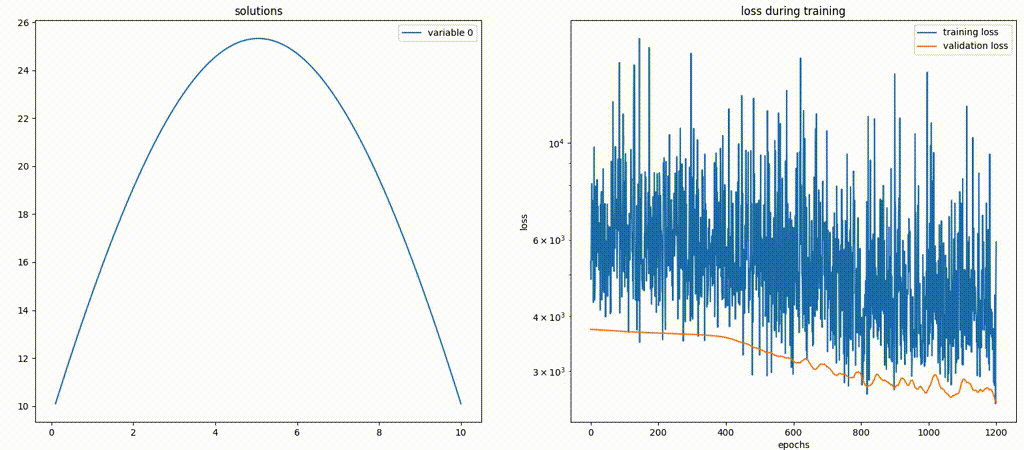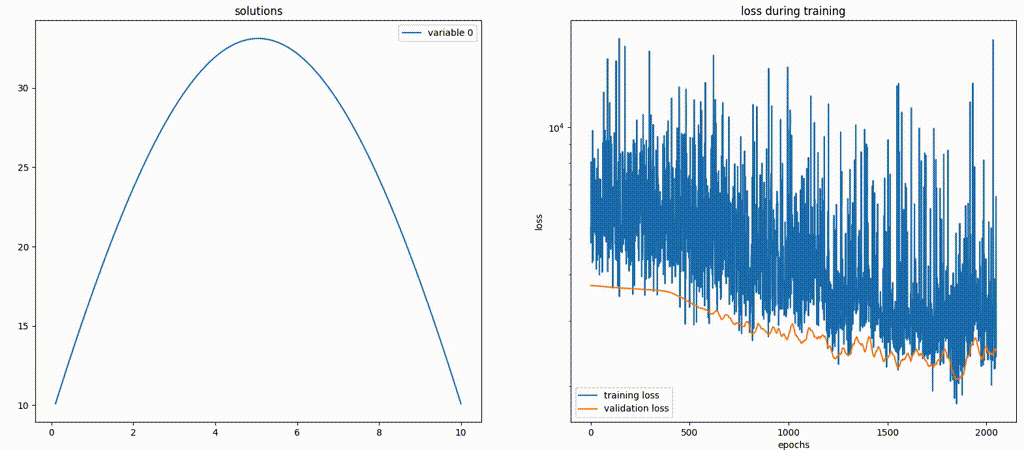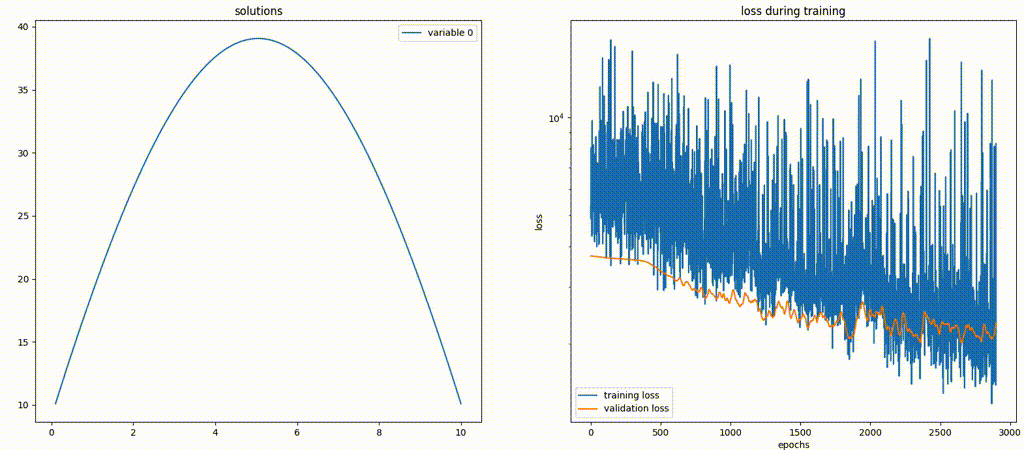 y-direction. The latter can be deduced by the change of the maximum value of the y-axis over time.

[shuheng-liu]

Better reparameterization seems to do the trick.

A better solution can be obtained by using a Dirichlet Condition that fixes one end of the boundary and penalizes the boundary value on the other end (by adding an additional term to the loss).