There are two issues here:
-
You have commented out the measurement and conditional corrections on the ancilla qubits needed for teleportation. Without these the output state of the teleported qubit is effectively random.
-
The process tomography function cannot really handle a teleportation circuit as the function assumes you are preparing and measuring the same qubits. In tomography of a teleportation circuit your input states would be on qubit-0, and your final measurements would be on qubit-2. Where as the process tomography function is applying both the different input states and measurements to qubit-2, which is one of the teleportation ancilla that should be always prepared in 0.



Informations
What is the current behavior?
The process tomography for a teleported state seems providing awkward results. Conversely, state tomography for the same circuit works just fine
Specifically, this is the ideal Chi matrix for a X Gate.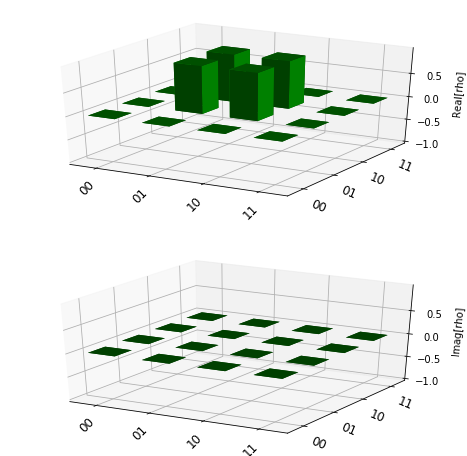
And this is the Chi matrix as output of process tomography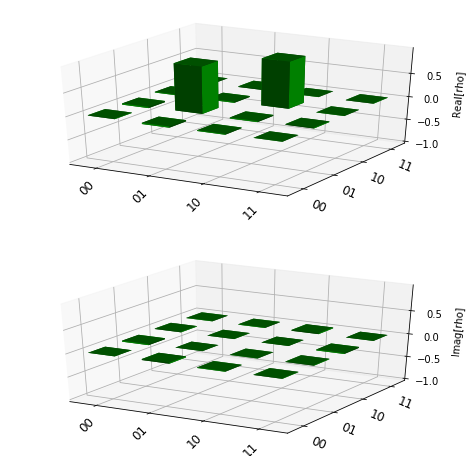
Steps to reproduce the problem
code.txt
What is the expected behavior?
returning a Chi matrix equal or close to id_choi
Suggested solutions