This is due to failed generation of latent space coordinates for a new field value (printed lots of nans).
Using a larger sigma helps, but still results in some invalid (nan) coordinates (notable here in interactive slider video).




Closed cchriste closed 4 years ago
This is due to failed generation of latent space coordinates for a new field value (printed lots of nans).
Using a larger sigma helps, but still results in some invalid (nan) coordinates (notable here in interactive slider video).




Here's the code used to compute the new latent space coordinate:
// z' = f(x', X, Z)
//
// new z_coord z' = Gaussian kernel regression computed from new field_val x' and original
// field_vals X along with their associated z_coords Z.
//
// The contribution of the nearby original z_coords is larger than those farther away using a
// Gaussian curve centered at the new sample, and sigma determines the width of this curve.
//
const Eigen::RowVectorXf Model::getNewLatentSpaceValue(const Eigen::RowVectorXf& fieldvalues, const Eigen::MatrixXf& z_coords, float new_fieldval, float sigma)
{
// 1 / sqrt(2*pi*sigma) * e^0.5*((x-mu)/sigma)^2
// x-mu is the differences between the new value existing field values
//
// sigma should be used to only include a subset of nearby fieldvalues to average its value
// is not independent of the field range, but perhaps a percentage of the data range is a
// reasonable choice (**todo: ask Shireen what she wants to do** :)
// gaussian kernel regression to generate a new LSV
using namespace Eigen;
// calculate difference
RowVectorXf fieldvals(fieldvalues);
fieldvals *= -1.0;
fieldvals.array() += new_fieldval;
// apply Gaussian to difference
fieldvals = fieldvals.array().square();
fieldvals /= (-2.0 * sigma * sigma); /// <--- fieldvals can get really big cuz of this
fieldvals = fieldvals.array().exp();
float denom = sqrt(2.0 * M_PI * sigma);
fieldvals /= denom;
// calculate weight and normalization for regression
float summation = fieldvals.sum();
MatrixXf output = fieldvals * z_coords;
output /= summation;
return output;
}@sheryjoe Here are some of the questions I meant to ask you (as noted in the code :): Would normalizing the field values first help? Should we restrict minimum sigma?
Two comments on the code:
float denom = sqrt(2.0 M_PI sigma);
should be
float denom = sqrt(2.0 M_PI) sigma;
And I would add an epsilon as a safe guard to avoid dividing by zero
output /= (summation + epsilon); // epsilon ~ 1e-5
@sheryjoe Here are some of the questions I meant to ask you (as noted in the code :): Would normalizing the field values first help?
field values don't have to be normalized. Summation should normalize the weights on different samples to sum up to 1
Should we restrict minimum sigma?
Sigma can be set as factor * average min distance between given field values (QoI). This way, we can avoid too small sigmas unless crystals are degenerate (min = max). The factor can be chosen as in a 1 to 3 range.
This can be implemented as:
BTW, on dSpaceX front-end, you could have this factor as a user input to control how narrow or wide the kernel is, yet still internally sigma will be adaptable to how the field values within each crystal are distributed.
BTW, on dSpaceX front-end, you could have this factor as a user input to control how narrow or wide the kernel is, yet still internally sigma will be adaptable to how the field values within each crystal are distributed.
This is exactly what I was hoping could be done for the user.
Two comments on the code:
float denom = sqrt(2.0 M_PI sigma);
should be
float denom = sqrt(2.0 M_PI) sigma;
And I would add an epsilon as a safe guard to avoid dividing by zero
output /= (summation + epsilon); // epsilon ~ 1e-5
Thanks for the correction and advice to avoid div by 0.
Works beautifully!


For some of our datasets, the PCA models generated by our data processing pipeline have errors. Some of the interpolations fail and simply generate a black image. This video shows the issue for the current Cantilever Beam June 2020 dataset: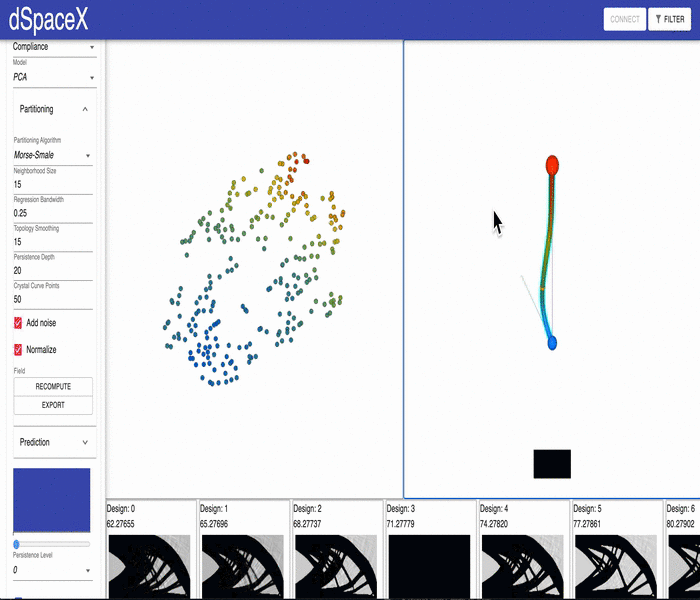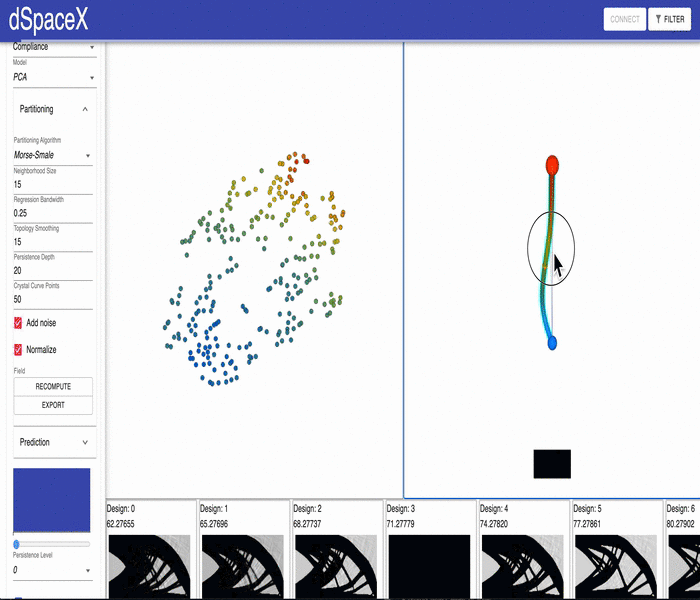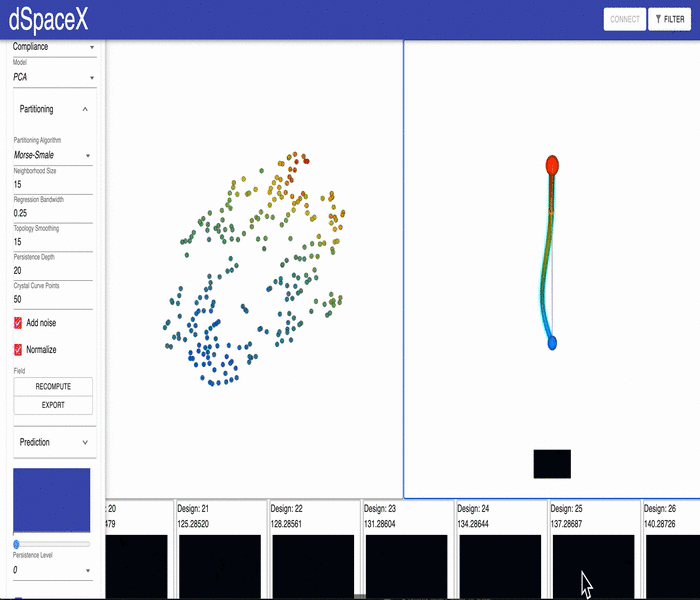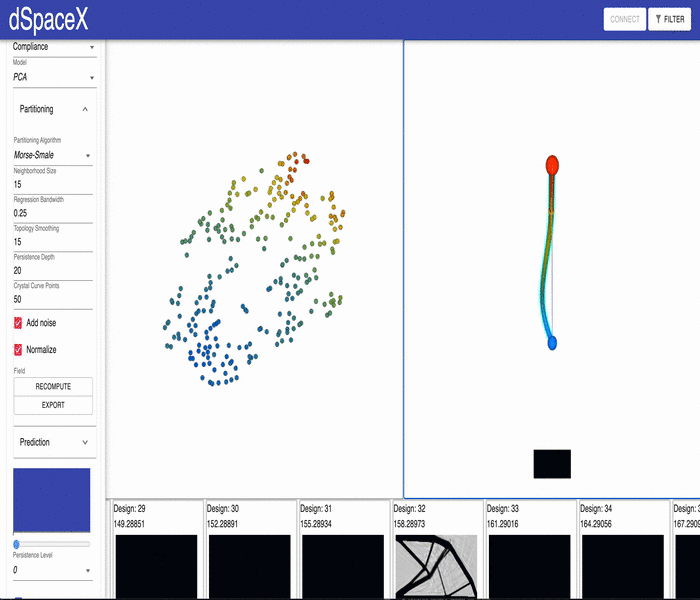
May be related to #188.