It looks like it's just FastChain here. MWE:
using OrdinaryDiffEq, StochasticDiffEq, DelayDiffEq, Flux, DiffEqFlux,
Zygote, Test, DiffEqSensitivity
mp = Float32[0.1,0.1]
x = Float32[2.; 0.]
xs = Float32.(hcat([0.; 0.], [1.; 0.], [2.; 0.]))
tspan = (0.0f0,1.0f0)
dudt = Chain(Dense(2,50,tanh),Dense(50,2))
dudt2 = Chain(Dense(2,50,tanh),Dense(50,2))
NeuralDSDE(dudt,dudt2,(0.0f0,.1f0),SOSRI(),saveat=0.1)(x)
sode = NeuralDSDE(dudt,dudt2,(0.0f0,.1f0),SOSRI(),saveat=0.0:0.01:0.1)
grads = Zygote.gradient(()->sum(sode(x)),Flux.params(x,sode))
@test ! iszero(grads[x])
@test ! iszero(grads[sode.p])
@test ! iszero(grads[sode.p][end])
dudt = FastChain(FastDense(2,50,tanh),FastDense(50,2))
dudt2 = FastChain(FastDense(2,50,tanh),FastDense(50,2))
NeuralDSDE(dudt,dudt2,(0.0f0,.1f0),SOSRI(),saveat=0.1)(x)
sode = NeuralDSDE(dudt,dudt2,(0.0f0,.1f0),SOSRI(),saveat=0.0:0.01:0.1)
grads = Zygote.gradient(()->sum(sode(x)),Flux.params(x,sode))
@test ! iszero(grads[x])
@test ! iszero(grads[sode.p][end])
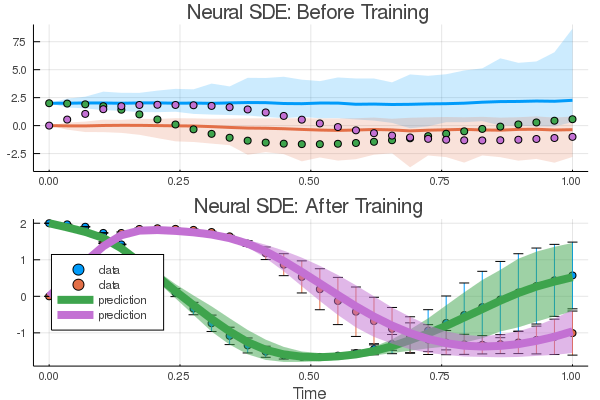
By running the neural SDE example in the docs, the result of
sciml_trainfor the diffusion parameters are the same as the starting point (see below). I don't know why that's the case but the reason seems to be thatZygotegives a zero gradient for those parameters.