A few comments. I believe you intended to implement a zero-order hold as opposed to first-order hold? In any case, I think the implementation U(y) ~ u would model a unit delay? I.e.,
y(t+dt) = u(t)what you'd really like is to communicate (pseudo code)
y(t to (t+dt)) = u(t)but there is currently no way to do this. The semantics for hybrid systems (both discrete and continuous) is still on the discussion stage https://github.com/SciML/ModelingToolkit.jl/issues/894
The way Modelica does this is with the when block in combination with the previous/pre operator (similar to DiscreteUpdate) like so
when {sampleTrigger, initial()} then
ySample = u;
end when;
y = pre(ySample);
Consider the following model:
The solution is incorrect: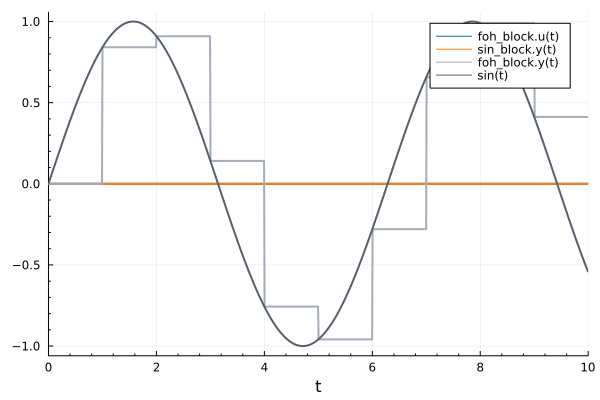
Although
zoh_block₊y(t)is correct, the other two (zoh_block₊u(t)andsin_block₊y(t)) are wrong (constant to zero).