So the preliminary accuracy/performance analysis comparison with Expokit is here:
https://gist.github.com/MSeeker1340/5f5f9f1333824ee7aa7052b98a0e6dc2
The results are... a bit alarming, at least for big h. It seems that if the size of Krylov subspace is small then our non-subdividing implementation performs rather poorly.
Of course, when you look at the performance analysis, you can see that Expokit spends much more time in the case of large h because of the subdividing. But the gap in accuracy is just too big to justify using the non-subdividing version. It turns out Expokit's approach does make sense after all.
Now, say that we switch back to using Expokit's subdivision approach. Then the problem would be how to formulate a time-stepping method analogous to what Expokit does in the case of phimv to higher order phi functions. Guess it's time to start doing some algebra then.
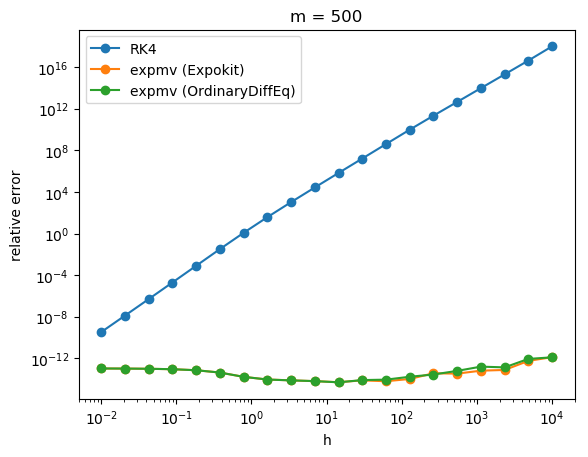
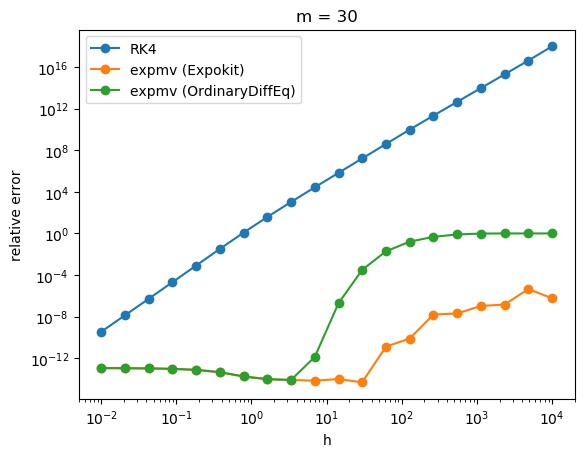
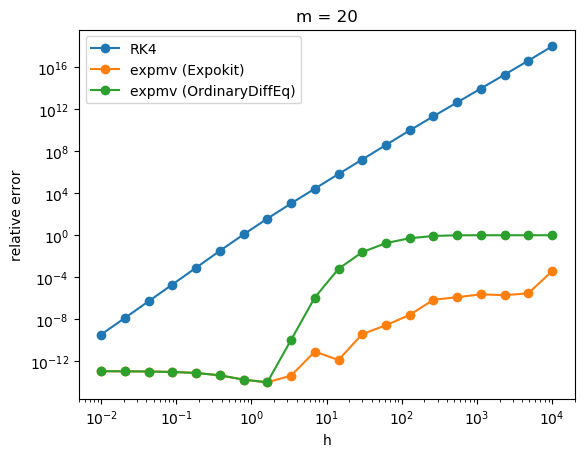
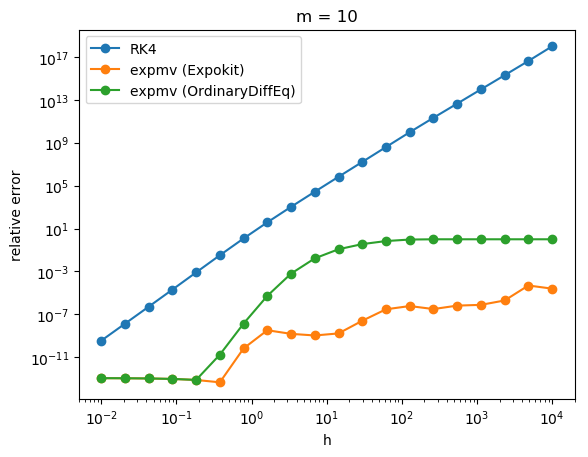


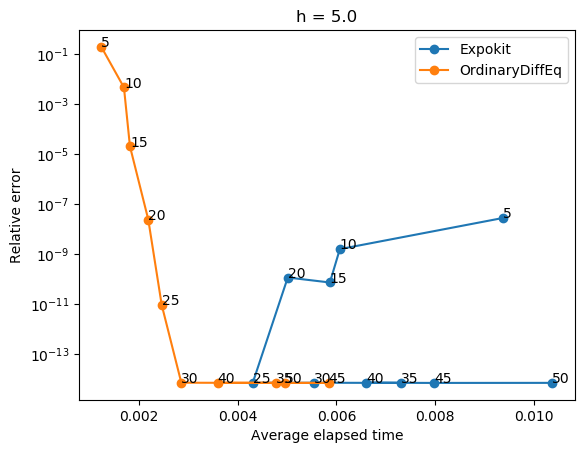
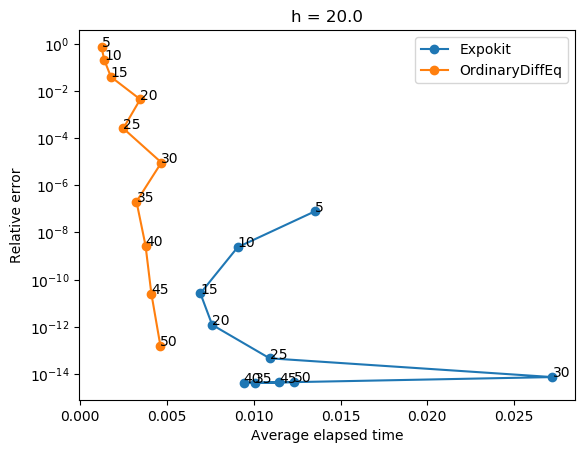
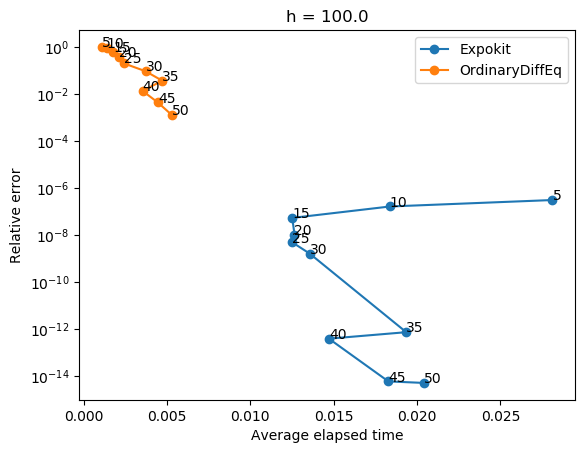



I think there's still some things to investigate.
@MSeeker1340