复习概要
一、引言
- 密钥体制组成
- 明文、密文、密钥、加密算法、解密算法
- 好的密钥体制
- 两类计算容易
- 已知明文和加密密钥
- 已知密文和解密密钥
- 一个不能
- 不知道解密密钥时,不能由密文推知明文
- 两类计算容易
- 攻击分析密码体制方法与应对方法
- 穷举攻击 $\rightarrow $增大密钥量
- 统计分析攻击 $\rightarrow $使得明文与密文的统计特征不一样
- 解密变换攻击 $\rightarrow $选择足够复杂的加密算法
- 攻击的分类
- 自然攻击
- 自然灾害、电磁辐射、电磁干扰
- 人为攻击
- 外部攻击
- 被动攻击
- 内容信息获取(1)
- 数据业务流分析(2)
- 主动攻击
- 伪造(3)
- 篡改:内容修改(4)、顺序修改(5)、计时修改(6)
- 外部攻击
- 发送方否认(7)
- 接收方否认(8)
- 外部攻击
- 安全措施
- 数据保密:(1)(2)
- 消息认证:(3)(4)(5)(6)
- 数字签名:(7)(8)和部分的(3)(4)(5)(6)
- 自然攻击
- 安全攻击的形式
- 中断
- 截取
- 伪造
- 篡改
- 重放
- 密码分析分类
- 唯密文攻击:只知道一些密文
- 已知明文攻击:知道一些明文密文对
- 选择明文攻击:任意明文 $\rightarrow $密文
- 选择密文攻击:任意密文 $\rightarrow $明文
- 选择文本攻击:任意明文 $\leftrightarrow $任意密文
- 密码体制分类
- 单钥密码体制
- 流密码
- 分组密码
- 双钥密码体制
- 加密密钥和解密密钥不同,DF提出,公钥k1与私钥k2
- 用户A用自己的私钥 $k_{A2} $对消息m进行专用变换: $c=D{k_{A_2}} $,将c给用户B
- 用户B验证m使用: $$m=E{k{A1}}(c)=E{k_{A1}}(D{k_{A_2}}) $$
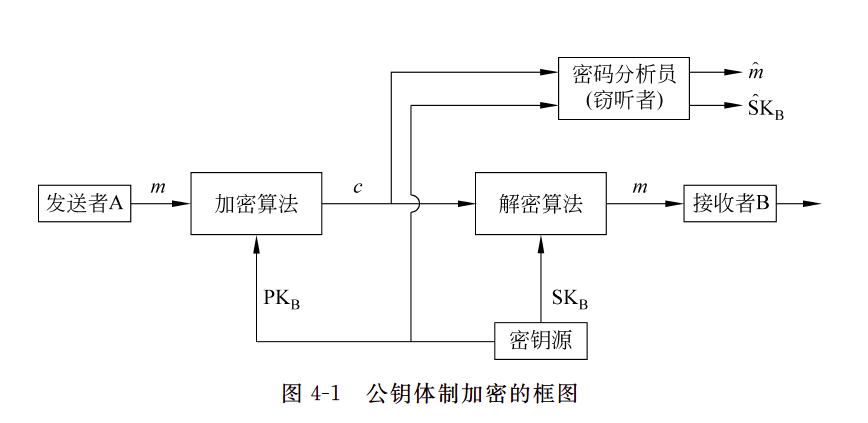
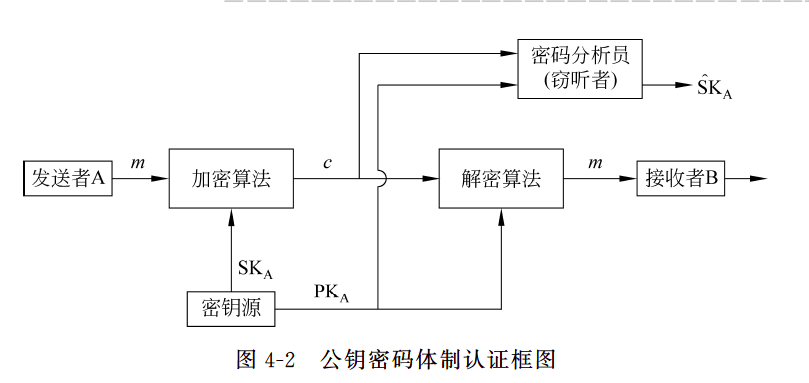
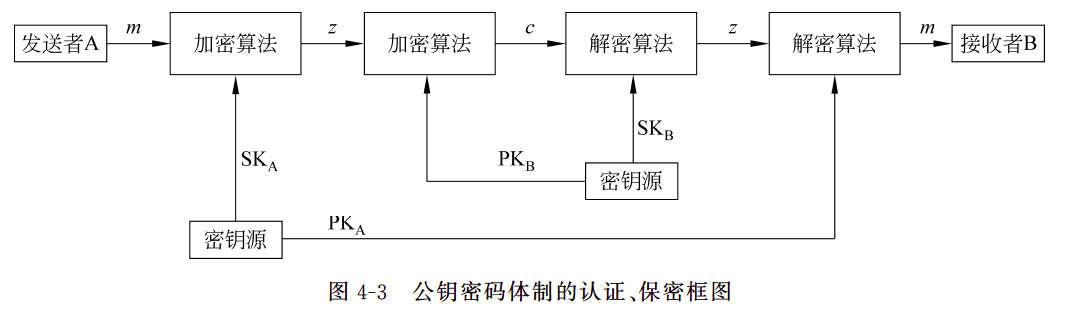
- 双钥保密和认证体制
- 为了同时实现保密性和准确性,可以采用双重加解密
graph LR; A(用户A)--m-->DkA2; DkA2-->EkB1; EkB1-->DkB2; DkB2-->EkA1; EkA1--m-->B(用户B); DkA2--认证-->EkA1; EkB1--保密-->DkB2;
- 为了同时实现保密性和准确性,可以采用双重加解密
- 单钥密码体制

现代密码学目录(仅目录)
1. 基础
1.1 威胁
1.2 信息安全模型
1.3 密码学基本概念
1.4 古典密码
2. 流密码
2.1 基本概念
2.2 线性反馈移位寄存器
2.3 线性移位寄存器的一元多项式表达式
2.4 m序列的伪随机性
2.5 m序列密码的破译
2.6 非线性序列
3. 分组密码体制
3.1 概述
3.2 数据加密标准
3.3 差分密码分析与线性密码分析
3.4 分组密码的运行模式
3.5 IDEA
3.6 AES|Rijindael
3.7 SM4
3.8 祖冲之
4. 公钥密码
4.1 数学知识
4.2 基本概念
4.3 RSA
4.4 背包密码体制
4.5 NTRU
4.6 椭圆曲线密码体制
4.7 SM2椭圆曲线公钥密码加密算法
5. 密钥分配与密钥管理
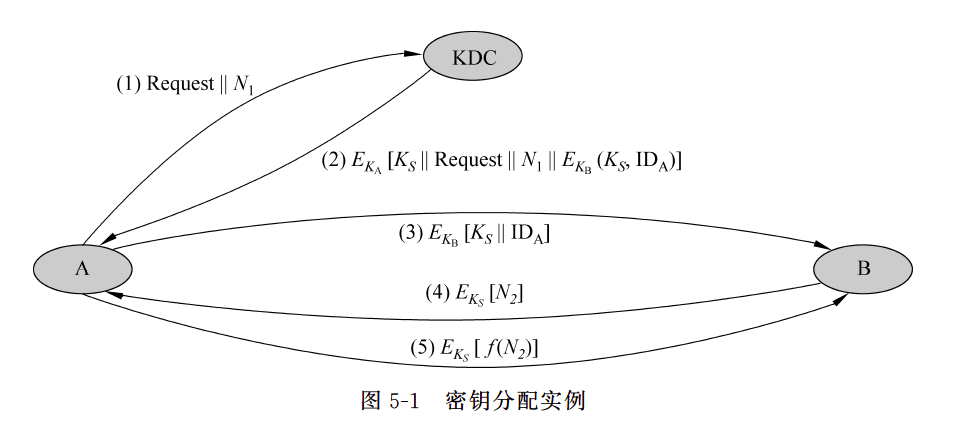
5.1 单钥加密体制的密钥分配
5.2 公钥加密体制的密钥分配
5.3 随机数的产生
5.4 秘密分割
6. 消息认证与哈希函数
6.1 消息认证
6.2 哈希函数
6.3 MD5
6.4 安全哈希算法
6.5 HMAC
6.6 SM3
7. 数字签名和认证协议
7.1 基本概念
7.2 数字签名标准
7.3 其他签名方案
7.4 SM2椭圆曲线公钥密码签名算法
7.4 认证协议
8. 密码协议
8.1 基本协议
8.2 零知识证明
8.3 安全多方计算
9. 可证明安全
9.1 语义安全的公钥密码体制定义
9.2 语义安全的RSA的加密方案
9.3 Paillier公钥密码系统
9.4 Cramer-Shoup密码系统
9.5 RSA-FDH签名方案
9.6 BLS短签名方案
9.7 基于身份的密码体制
10. 网络加密与认证
10.1 网络通信加密
10.2 Kerberos认证系统
10.3 X.509认证业务
10.4 PGP