代码随想录算法训练营 Day35 贪心算法V

435. 无重叠区间

题目链接：

[435. 无重叠区间 - 力扣（LeetCode）](https://leetcode.cn/problems/non-overlapping-intervals/description/)

题目描述：

给定一个区间的集合 intervals ，其中 intervals[i] = [starti, endi] 。返回 需要移除区间的最小数量，使剩余区间互不重叠 。

思路1

这个题目与上一个打爆气球的差不多，这里只要用总数减去之前的箭的数量，即可得到需要移除的最少数目了。为什么这样是可行的呢？首先要注意这里减去的其实是弓箭的数量就相当于是非交叉区间的数量。所有的减去非交叉的就是交叉的数量，也就是我们要求的。

class Solution {
    public int eraseOverlapIntervals(int[][] intervals) {
        Arrays.sort(intervals,(p1,p2) -> {
            return Integer.compare(p1[0], p2[0]);
        });
        int count  = 1;
        for (int i = 1; i < intervals.length; i++) {
            if(intervals[i][0] >= intervals[i-1][1]){
                count++;
            }else{
                intervals[i][1] = Math.min(intervals[i][1], intervals[i - 1][1]); 
            }
        }
        return intervals.length - count;
    }
}

思路2

这里的贪心思想体现在，选取长度最小的区间进行保留，因为长的区间覆盖的范围大于短的，局部贪心就是有充分的优先去除长的，保留短的。局部最优推出全局最优。

这里使用end来标记重复区间内最短的区间终止位置，并与下一个区间的起始位置进行比较。

class Solution {
    public int eraseOverlapIntervals(int[][] intervals) {
        Arrays.sort(intervals, (a,b) -> Integer.compare(a[0],b[0]));
        int count = 0;
        int end = intervals[0][1];
        for(int i = 1; i < intervals.length; i++){
            if(intervals[i][0] < end){
                count++;
                end = Math.min(end, intervals[i][1]);
            }else{
                end = intervals[i][1];
            }
        }
        return count;
    }
}

763. 分字母区间

题目链接：

[763. 划分字母区间 - 力扣（LeetCode）](https://leetcode.cn/problems/partition-labels/description/)

题目描述：

给你一个字符串 s 。我们要把这个字符串划分为尽可能多的片段，同一字母最多出现在一个片段中。

注意，划分结果需要满足：将所有划分结果按顺序连接，得到的字符串仍然是 s 。

返回一个表示每个字符串片段的长度的列表。

思路

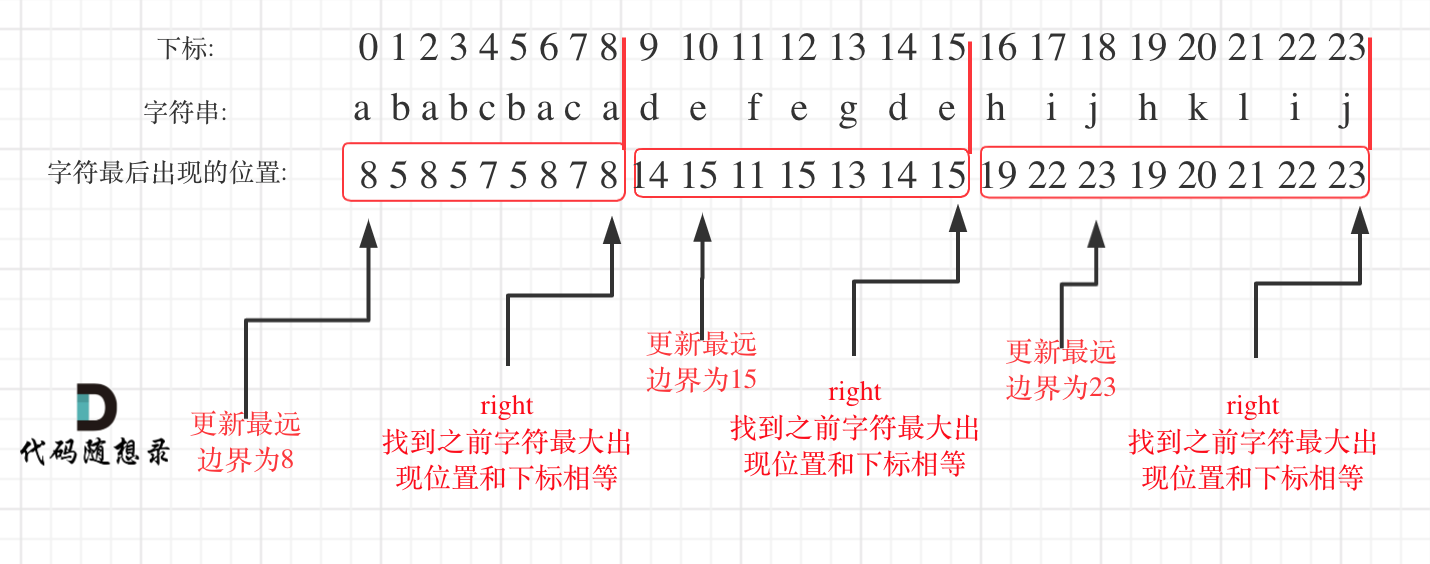
763.划分字母区间

上图就能很好的体现这道题的思路，就是记录每个字母出现的最远位置，然后通过两个下标来记录长度，依次遍历当出现比现在的最远边界还要大的就说明我们现在不得不包含一个距离更远的字母，这时更新新的要到达的字母，以此类推，同时贪心的思想也在这里，就是尽可能的不包含更远的字母，除非还没到当前的这个字母的最远位置不得已包括了新的更远的字母。

这里使用一个数组来记录各个字母的最远位置，然后在进行一次遍历，当还没有到达当前字母最远的位置时，要与每个新字母进行判断，看这个新字母的最远位置，是否大于当前的字母位置，如果大于当前字母，就以更大的这个为标准，更新right位置，直到遍历到right，最后将right-left+1记录到结果中，并更新left位置到下一段的开始位置，即right+1。

class Solution {
    public List<Integer> partitionLabels(String s) {
        List<Integer> list = new LinkedList<>();
        int[] count  = new int[26];
        for(int i = 0; i < s.length(); i++){
            count[s.charAt(i)-'a'] = i;
        }
        int left = 0;
        int right = 0;
        for(int i = 0; i < s.length(); i++){
            right = Math.max(right, count[s.charAt(i) - 'a']);
            if(i == right){
                list.add(right - left + 1);
                left = i+1;
            }
        }
        return list;
    }   
}

56. 合并区间

题目链接：

[56. 合并区间 - 力扣（LeetCode）](https://leetcode.cn/problems/merge-intervals/description/)

题目描述：

以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回 一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间 。

思路

这个题目与之前的重叠区间的思路差别不大，判断区间重贴后要进行区间合并。所以一样的套路，先排序，让所有的相邻区间尽可能的重叠在一起，合并区间后左边界和右边界，作为一个新的区间，加入到result数组里就可以了。如果没有合并就把原区间加入到result数组。

class Solution {
    public int[][] merge(int[][] intervals) {
        Arrays.sort(intervals,(a,b) -> Integer.compare(a[0], b[0]));
        List<int[]> res = new LinkedList<>();
        int left = intervals[0][0];
        int right = intervals[0][1];
        for(int i = 1; i < intervals.length; i++){
            if(intervals[i][0] <= right){
                right = Math.max(intervals[i][1] ,right);
            }else{
                res.add(new int[]{left, right});
                left = intervals[i][0];
                right = intervals[i][1];
            }
        }
        res.add(new int[]{left, right});
        return res.toArray(new int[res.size()][]);
    }
}

TerminalStation / Bert-Blog