Open YinLiu-91 opened 11 months ago
链接中的如下值,是根据 #6 中介绍的公式计算的:
$u_l=c_0-c_1+\frac{2}{3}\cdot c_2$
$u_m=c_0-\frac{1}{3}c_2$
$u_r=c_0+c_1+\frac{2}{3}\cdot c_2$
从chiwang shu 的天元课程讲义中有(注意,均值是对 $uh=c_0+c_1x+c_2(x^2-1/3)$ 在-1,1上积分平均的结果,不是三个点的值简单相加再相除),经过积分后, $\bar{u}_i=c_0$ :
那么: $u_{i+1/2}-\bar{u}_i=c_0+c_1+\frac{2}{3}\cdot c_2-(c_0)=c_1+2/3c_2$
且: $\bar{u}_{i}-u=c_1-2/3c_2$ 截图中第二项好像不太对?
因此利用下图公式可以得到 $c_1=\frac{minmod_1+minmod_2}{2}, c_2=\frac{3}{4}(minmod_1-minmod_2)$,即如下代码中的uhmod(i,2),uhmod(i,3)
for i = 1:Nx % 循环所有单元 deltaUR = uh(i,2) + (2/3)*uh(i,3); % 单元右端值减去平均值 deltaUL = uh(i,2) - (2/3)*uh(i,3); % 单元平均值减去单元左端值?这里对? deltaURM = uhb(i + 2,1) - uhb(i + 1,1); % 右单元平均值减去本单元平均值 deltaULM = uhb(i + 1,1) - uhb(i,1); % 本单元平均值减去左单元平均值
deltaURM1 = minmod(deltaUR,deltaURM,deltaULM); deltaULM1 = minmod(deltaUL,deltaURM,deltaULM);
uhmod(i,2) = (deltaURM1 + deltaULM1)/2; uhmod(i,3) = 3*(deltaURM1 - deltaULM1)/4; end
链接中的如下值,是根据 #6 中介绍的公式计算的:
$u_l=c_0-c_1+\frac{2}{3}\cdot c_2$
$u_m=c_0-\frac{1}{3}c_2$
$u_r=c_0+c_1+\frac{2}{3}\cdot c_2$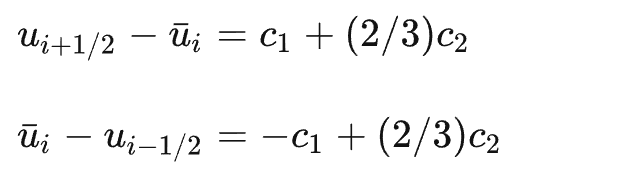
从chiwang shu 的天元课程讲义中有(注意,均值是对 $uh=c_0+c_1x+c_2(x^2-1/3)$ 在-1,1上积分平均的结果,不是三个点的值简单相加再相除),经过积分后, $\bar{u}_i=c_0$ :
那么: $u_{i+1/2}-\bar{u}_i=c_0+c_1+\frac{2}{3}\cdot c_2-(c_0)=c_1+2/3c_2$
且: $\bar{u}_{i}-u=c_1-2/3c_2$ 截图中第二项好像不太对?
因此利用下图公式可以得到 $c_1=\frac{minmod_1+minmod_2}{2}, c_2=\frac{3}{4}(minmod_1-minmod_2)$,即如下代码中的uhmod(i,2),uhmod(i,3)
deltaURM1 = minmod(deltaUR,deltaURM,deltaULM); deltaULM1 = minmod(deltaUL,deltaURM,deltaULM);
uhmod(i,2) = (deltaURM1 + deltaULM1)/2; uhmod(i,3) = 3*(deltaURM1 - deltaULM1)/4; end