Open Yukyukuon opened 3 years ago
栅格化一个三角形
在屏幕上画出一个实心三角形。在上一次作业中,在视口变化之后,我们调用了函数rasterize_wireframe(const Triangle& t)。但这一次,需要自己填写并调用函数rasterize_triangle(const Triangle& t)。
可通过叉乘(cross product)判断线在线的左和右,点在三角形的内和外。
static bool insideTriangle(int x, int y, const Vector3f* _v) { // TODO : Implement this function to check if the point (x, y) is inside the triangle represented by _v[0], _v[1], _v[2] Eigen::Vector2f p; p << x, y; Eigen::Vector2f AB = _v[1].head(2) - _v[0].head(2); Eigen::Vector2f BC = _v[2].head(2) - _v[1].head(2); Eigen::Vector2f CA = _v[0].head(2) - _v[2].head(2); Eigen::Vector2f AP = p - _v[0].head(2); Eigen::Vector2f BP = p - _v[1].head(2); Eigen::Vector2f CP = p - _v[2].head(2); return AB[0] * AP[1] - AP[0] * AB[1] > 0 && BC[0] * BP[1] - BP[0] * BC[1] > 0 && CA[0] * CP[1] - CP[0] * CA[1] > 0; } // 老师的 static bool insideTriangle(int x, int y, const Vector4f* _v){ Vector3f v[3]; for(int i=0;i<3;i++) v[i] = {_v[i].x(),_v[i].y(), 1.0}; Vector3f f0,f1,f2; f0 = v[1].cross(v[0]); f1 = v[2].cross(v[1]); f2 = v[0].cross(v[2]); Vector3f p(x,y,1.); if((p.dot(f0)*f0.dot(v[2])>0) && (p.dot(f1)*f1.dot(v[0])>0) && (p.dot(f2)*f2.dot(v[1])>0)) return true; return false; }
实际情况下,并不用检测全部Pixels,使用包围盒。 取三角形的三个点P0,P1,P2的
Z-buffering 深度缓存
1.记录每个像素的z-buffer值,每个位置初始值设为无穷大 -(frame buffer stores color values) -(depth buffer [z-buffer] stores depth)
2.遍历三角形上的每一个像素点[x,y]如果该像素点的深度值z,小于zbuffer[x,y]中的值,则更新zbuffer[x,y]值为该店深度值z,并同时更新该像素点[x,y]的颜色为该三角形上的该点的颜色。
给定空间内三角形的三个顶点A,B,C三个点,必定唯一存在三个数α,β,γ满足: α + β + γ = 1 P(x, y) = αA + βB + γC
如果A点挂重物α,B点挂重物β,C点挂重物γ,则P点正好是重心。如果把P点放避雷针上,能保持平衡:
Warning: 投影后的重心坐标会变,所以是取三维空间中的坐标来求插值
//求重心坐标 static std::tuple<float, float, float> computeBarycentric2D(float x, float y, const Vector3f* v) { float c1 = (x*(v[1].y() - v[2].y()) + (v[2].x() - v[1].x())*y + v[1].x()*v[2].y() - v[2].x()*v[1].y()) / (v[0].x()*(v[1].y() - v[2].y()) + (v[2].x() - v[1].x())*v[0].y() + v[1].x()*v[2].y() - v[2].x()*v[1].y()); float c2 = (x*(v[2].y() - v[0].y()) + (v[0].x() - v[2].x())*y + v[2].x()*v[0].y() - v[0].x()*v[2].y()) / (v[1].x()*(v[2].y() - v[0].y()) + (v[0].x() - v[2].x())*v[1].y() + v[2].x()*v[0].y() - v[0].x()*v[2].y()); float c3 = (x*(v[0].y() - v[1].y()) + (v[1].x() - v[0].x())*y + v[0].x()*v[1].y() - v[1].x()*v[0].y()) / (v[2].x()*(v[0].y() - v[1].y()) + (v[1].x() - v[0].x())*v[2].y() + v[0].x()*v[1].y() - v[1].x()*v[0].y()); return {c1,c2,c3}; }
透视矫正插值这地方参考:https://zhuanlan.zhihu.com/p/144331875 (写的太好了!!!!!!)
//重心坐标转到投影后的二维面上,透视矫正插值 auto[alpha, beta, gamma] = computeBarycentric2D(x, y, t.v); float w_reciprocal = 1.0/(alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w()); float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w(); z_interpolated *= w_reciprocal;
对每一个Pixel分成多个小Pixels。 算法是将每一个像素划分成许多小像素,每一个小像素有一个中心,我们可以判断这些点在三角形内,再将这些点平均起来,如果点足够多就能得到比较好的结果。其实就是在一个像素内部增加采样点。例如一个像素里,如果4个采样点都不在三角形内,就判定它不在三角形内,如果有一个采样点在三角形内,覆盖率就为25%,如果三个点在,覆盖率就为75%。通过这样的方法就能实现抗锯齿的效果。
// 光栅化函数 void rst::rasterizer::rasterize_triangle(const Triangle& t) { auto v = t.toVector4(); auto x_min = std::min(v[0][0], std::min(v[1][0], v[2][0])); auto x_max = std::max(v[0][0], std::max(v[1][0], v[2][0])); auto y_min = std::min(v[0][1], std::min(v[1][1], v[2][1])); auto y_max = std::max(v[0][1], std::max(v[1][1], v[2][1])); x_min = (int)std::floor(x_min); x_max = (int)std::ceil(x_max); y_min = (int)std::floor(y_min); y_max = (int)std::ceil(y_max); bool MSAA = true; //是否开启MSAA if(MSAA) { std::vector<Eigen::Vector2f> pos { {0.25, 0.25}, {0.75, 0.25}, {0.25, 0.75}, {0.75, 0.75}, }; for(int x = x_min; x <= x_max; x++) { for(int y = y_min; y <= y_max; y++) { float minDepth = FLT_MAX; //记录最小深度 int count = 0; for(int i = 0; i < 4; i++) //判断MSAA的小点是否在三角形内部 { if(insideTriangle((float)x + pos[i][0], (float)y + pos[i][1], t.v)) { count++; auto tup = computeBarycentric2D((float)x + pos[i][0], (float)y + pos[i][1], t.v); float alpha, beta, gamma; std::tie(alpha, beta, gamma) = tup; float w_reciprocal = 1.0/(alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w()); float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w(); z_interpolated *= w_reciprocal; minDepth = std::min(minDepth, z_interpolated); } } if(count != 0) { if(depth_buf[get_index(x, y)] > minDepth) { Vector3f color = t.getColor() * count / 4.0; Vector3f point(3); point << (float)x, (float)y, minDepth; //替换深度 depth_buf[get_index(x, y)] = minDepth; //修改颜色 set_pixel(point, color); } } } } } else { for(int x = x_min; x <= x_max; x++) { for(int y = y_min; y <= y_max; y++) { if(insideTriangle(x + 0.5, y + 0.5, t.v)) { auto[alpha, beta, gamma] = computeBarycentric2D(x, y, t.v); float w_reciprocal = 1.0/(alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w()); float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w(); z_interpolated *= w_reciprocal; if(depth_buf[get_index(x, y)] > z_interpolated) { Vector3f color = t.getColor(); Vector3f point(3); point << (float)x, (float)y, z_interpolated; depth_buf[get_index(x, y)] = z_interpolated; set_pixel(point, color); } } } } } }
结果图之后补上
GAMES101(作业2)
栅格化一个三角形
作业描述
在屏幕上画出一个实心三角形。在上一次作业中,在视口变化之后,我们调用了函数rasterize_wireframe(const Triangle& t)。但这一次,需要自己填写并调用函数rasterize_triangle(const Triangle& t)。
该函数的内部工作工作流程如下
要点
1.判断是否在三角形内
可通过叉乘(cross product)判断线在线的左和右,点在三角形的内和外。
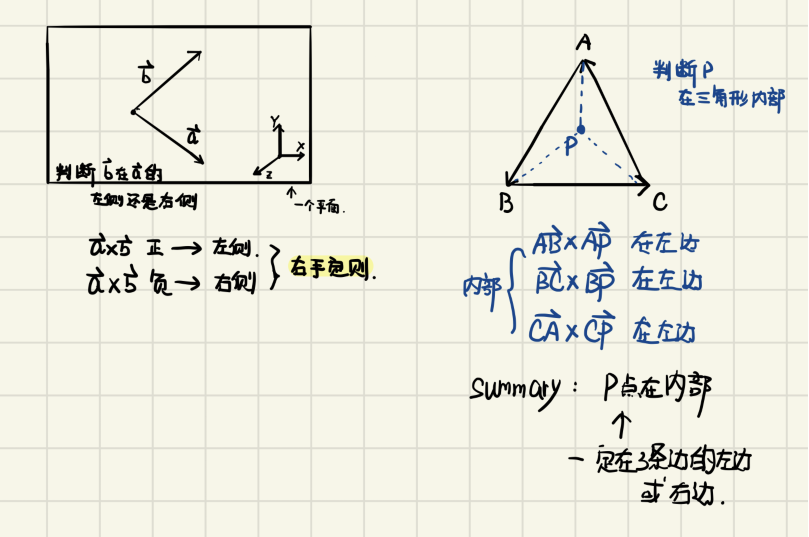
2.Bounding Box(包围盒)
实际情况下,并不用检测全部Pixels,使用包围盒。
取三角形的三个点P0,P1,P2的
3.Z-Buffer算法
Z-buffering 深度缓存
1.记录每个像素的z-buffer值,每个位置初始值设为无穷大
-(frame buffer stores color values)
-(depth buffer [z-buffer] stores depth)
2.遍历三角形上的每一个像素点[x,y]如果该像素点的深度值z,小于zbuffer[x,y]中的值,则更新zbuffer[x,y]值为该店深度值z,并同时更新该像素点[x,y]的颜色为该三角形上的该点的颜色。
4.重心坐标(Barycentric Coordinates)
定义
给定空间内三角形的三个顶点A,B,C三个点,必定唯一存在三个数α,β,γ满足:
α + β + γ = 1
P(x, y) = αA + βB + γC
求解
如果A点挂重物α,B点挂重物β,C点挂重物γ,则P点正好是重心。如果把P点放避雷针上,能保持平衡:
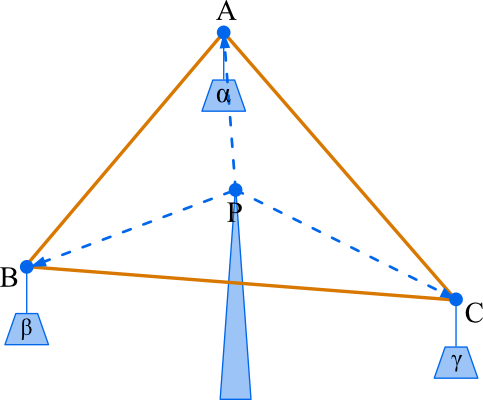
Warning: 投影后的重心坐标会变,所以是取三维空间中的坐标来求插值
透视矫正插值这地方参考:https://zhuanlan.zhihu.com/p/144331875
(写的太好了!!!!!!)
4.反走样 Antialising By Supersampling
MSAA
对每一个Pixel分成多个小Pixels。 算法是将每一个像素划分成许多小像素,每一个小像素有一个中心,我们可以判断这些点在三角形内,再将这些点平均起来,如果点足够多就能得到比较好的结果。其实就是在一个像素内部增加采样点。例如一个像素里,如果4个采样点都不在三角形内,就判定它不在三角形内,如果有一个采样点在三角形内,覆盖率就为25%,如果三个点在,覆盖率就为75%。通过这样的方法就能实现抗锯齿的效果。
Code
结果
结果图之后补上