anjia commented 2 years ago

87
- Number 在内存中的存储格式（有例子，如 168、0.125、0.1）
- Number 数值的精度损失是怎么产生的？
- 如何通俗地理解二进制浮点数的“精度损失”？
- IEEE 754 binary64 里的指数编码详解
- 5 种浮点异常：无效运算、除以零、上溢（指数太大）、下溢（指数太小）和不精确
为什么 toPrecision(17) 能让内存中的数值原形毕露？
- JavaScript 是如何读取并“正确”显示无限循环的有理数的，比如 0.1₍₁₀₎ = 0.0 0011 0011 0011 ...₍₂₎
- 详解 IEEE 754 binary64 为什么能提供十进制数 15\~17 个有效数精度
Number 的字面量表示：十进制、二进制、八进制、十六进制
如何理解 Number 里的 8 个常量：结合内存存储，理解它们的含义和值
- 最大正数 vs 最大安全整数
- 什么是安全整数
- 浮点数→实数：有间隔，且间隔不均匀
  - 在线性增长中，是 n 段等差数列，[最小差值, 最大差值]
  - 在指数增长中，有精度裁切，所以会跳跃
Number 对象

anjia commented 2 years ago

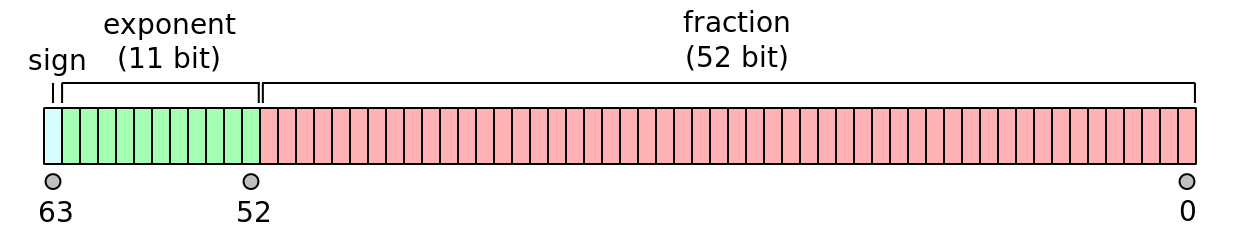
二. 为什么 `toPrecision(17)` 能让内存中的数值原形毕露？

通过上篇文章 #87 ，我们知道了双精度浮点数之所以会“损失精度”的根本原因。本文将在此基础上，继续探索编程语言（以 JavaScript 为例）是如何读取并显示内存中的 binary64 数据的。

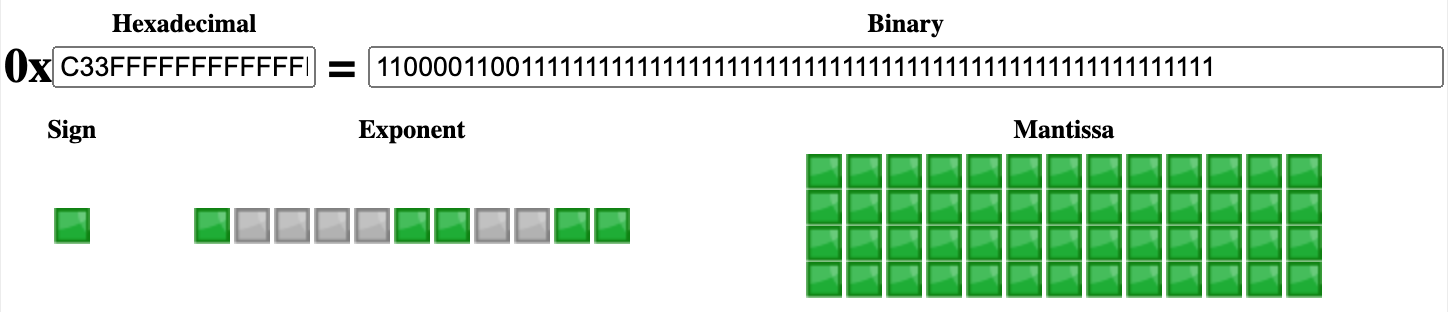
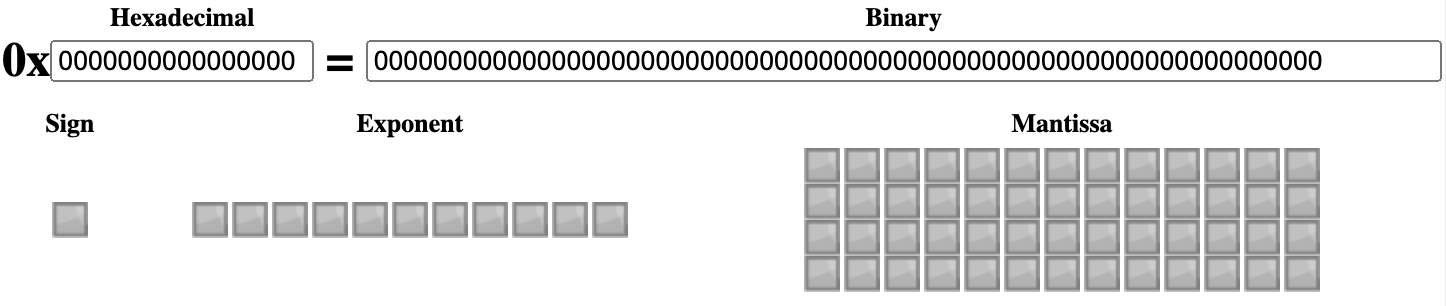
继续以十进制的 0.1 为例，我们知道了它在内存中存储的真实数值并不是 0.1 而是 0.100000000000000005551115123126。

0.1 的 IEEE 754 binary64 表示

但是，在我们的日常开发中，0.1 总会输出 0.1 而不是它在内存中的精确值。比如：

0.1; // 0.1
Number(0.1); // 0.1

除非我们手动指定精度。如下：

Number(0.1).toPrecision(); // '0.1', 参数为空则调 toString()
Number(0.1).toPrecision(16); // '0.1000000000000000'  = 0.1
Number(0.1).toPrecision(17); // '0.10000000000000001' > 0.1
Number(0.1).toPrecision(18); // '0.100000000000000006'
Number(0.1).toPrecision(19); // '0.1000000000000000056'
Number(0.1).toPrecision(20); // '0.10000000000000000555'
Number(0.1).toPrecision(21); // '0.100000000000000005551'
Number(0.1).toPrecision(55); // '0.1000000000000000055511151231257827021181583404541015625'
Number(0.1).toPrecision(70); // '0.1000000000000000055511151231257827021181583404541015625000000000000000'

说明：toPrecision() 方法返回的类型是字符串

若精度参数为空/未定义，则会调用 Number.toString() 方法

若精度不在 [1,100] 之间，则会抛出错误 RangeError

ECMA-262 只需要最多 21 位有效数字的精度

也就是说，在我们的日常使用中，浏览器会自动帮我们截取精度，以让显示的数值“看起来”是正确的。

那么，双精度浮点数是按照什么规则来截取精度值的呢？维基百科里这样写道：

The 53-bit significand precision gives from 15 to 17 significant decimal digits precision (2⁻⁵³ ≈ 1.11 × 10⁻¹⁶). If a decimal string with at most 15 significant digits is converted to IEEE 754 double-precision representation, and then converted back to a decimal string with the same number of digits, the final result should match the original string. If an IEEE 754 double-precision number is converted to a decimal string with at least 17 significant digits, and then converted back to double-precision representation, the final result must match the original number.

IEEE 754 binary64 里的 53 位有效数精度能提供十进制数的 15 到 17 个有效数精度。

如果将一个最多有 15 位有效数字的十进制字符串转成 IEEE 754 双精度表示，然后再转回有相同位数的十进制字符串，则最终的结果应该（should）会和原始字符串相匹配。

如果将一个 IEEE 754 双精度数值转成一个至少有 17 位有效数字的十进制字符串，然后再将它转回双精度表示，则最终的结果一定（must）会和原始数值相匹配。

大意就是：

存十进制数时，如果它的有效数的位数 ≤15，那么计算机就能（should）保证其“存&取”一致。
读内存里的 IEEE 754 binary64 时，如果十进制有效数的位数 ≥17，那么计算机就能（must）保证其“取&存”一致。

本文旨在讨论“JavaScript 是如何读取并显示内存中的 binary64 数据”的，所以我们只重点关注第 2 点，即：读内存中的数值时，只要十进制的有效数字是 17 个就能保证不出错（内存里存啥就显示啥）。

再来看几个例子感受下。

Number(0.2); // 0.2
Number(0.2).toPrecision(16); // '0.2000000000000000' = 0.2
Number(0.2).toPrecision(17); // '0.20000000000000001' > 0.2

Number(1.005); // 1.005
Number(1.005).toPrecision(16); // '1.005000000000000' = 1.005
Number(1.005).toPrecision(17); // '1.0049999999999999' < 1.005

那么，为什么“16”就能刚好让数值看起来是正确的，而“17”就是一个照妖镜呢？

在回答这个问题之前，我们先看下二进制的 n 个有效位表示成十进制是什么样子的。

当有效位逐个增加

为了更清晰地描述问题，我们将“纯整数”和“纯小数”分开讨论。

纯整数

当只有 1 个二进制有效位时 x：能表示 2 个十进制数，它们之间的差值是 1。如下：

二进制	十进制
0	0
1	1

当有 2 个二进制有效位时 xx：能表示 2² = 4 个十进制数，它们之间的差值是 1。如下：

二进制	十进制
00	0
01	1
10*	2*
11*	3*

* 表示多了一个有效位之后新增的数，新增了 2₍₁₀₎个，其高位均是 1₍₂₎

当有 3 个二进制有效位时 xxx：能表示 2³ = 8 个十进制数，它们之间的差值是 1。如下：

二进制	十进制
000	0
001	1
010	2
011	3
100*	4*
101*	5*
110*	6*
111*	7*

* 表示多了一个有效位之后新增的数，新增了 4₍₁₀₎ = 2² 个，其高位均是 1₍₂₎

综上，利用数学归纳法可得出结论：

当整数部分有 n 个二进制有效位时，可以表示 2ⁿ 个十进制数，且它们是个等差数列，差值是 1
每增加 1 个二进制有效位，就会新增 2^n-1 个十进制数（即高位为 1 的数字）

纯小数

当只有 1 个二进制有效位时 0.x：能表示 2 个十进制数，它们之间的差值是 2^-1 = 0.5。如下：

二进制	十进制
0.0	0
0.1	0.5

当有 2 个二进制有效位时 0.xx：能表示 2² = 4 个十进制数，它们之间的差值是 2^-2 = 0.25。如下：

二进制	十进制
0.00	0
0.01*	0.25*
0.10	0.5
0.11*	0.75*

* 表示多了一个有效位之后新增的数，新增了 2₍₁₀₎个，其末位均是 1₍₂₎

当有 3 个二进制有效位时 0.xxx：能表示 2³ = 8 个十进制数，它们之间的差值是 2^-3 = 0.125。如下：

二进制	十进制
0.000	0
0.001*	0.125*
0.010	0.25
0.011*	0.375*
0.100	0.5
0.101*	0.625*
0.110	0.75
0.111*	0.875*

* 表示多了一个有效位之后新增的数，新增了 4₍₁₀₎ = 2² 个，其末位均是 1₍₂₎

当有 4 个二进制有效位时 0.xxxx：能表示 2⁴ = 16 个十进制数，它们之间的差值是 2^-4 = 0.0625。如下：

二进制	十进制
0.0000	0
0.0001*	0.0625*
0.0010	0.125
0.0011*	0.1875*
0.0100	0.25
0.0101*	0.3125*
0.0110	0.375
0.0111*	0.4375*
0.1000	0.5
0.1001*	0.5625*
0.1010	0.625
0.1011*	0.6875*
0.1100	0.75
0.1101*	0.8125*
0.1110	0.875
0.1111*	0.9375*

* 表示多了一个有效位之后新增的数，新增了 8₍₁₀₎ = 2³ 个，其末位均是 1₍₂₎

综上，利用数学归纳法可得出结论：

当小数部分有 n 个二进制有效位时，可以表示 2ⁿ 个十进制数，且它们是个等差数列，差值是 2^-n，数列范围是 [2^-n, 1)。
- 与纯整数不同，二进制只能精准地表示一部分十进制小数
- 即 k / 2ⁿ，其中 0 ≤ k < (2ⁿ - 1)，k 是整数
- 而其它小数只能是一个无限逼近真实值的二进制值，随着 n 越来越大时
每增加 1 个二进制有效位，就会新增 2^n-1 个十进制数（即末位为 1 的数字）

小结

当有 n 个二进制有效位时，可以表示 2ⁿ 个十进制数，且会形成一个等差数列
- 整数部分的差值是 1
- 小数部分的差值是 2^-m，小数将是“不连续”的（相对整数而言）
每增加 1 个二进制有效位，就会新增 2^n-1 个十进制数

以上结论，可以借鉴到 IEEE 754 双精度浮点数上就是：

IEEE 754 双精度浮点数能表示的小数们只有少部分是精准无误的，其它的都只能是一个无限逼近真实值的二进制数值。
IEEE 754 双精度浮点数的精度只和 53 个有效位有关，和指数无关。因为当小数点向左移动 1 位（或者向右移动 52 位）时，53 个有效位均变成了小数部分（或者整数部分）。倘若再向左（或者向右）移动，只能让数的绝对值变得更小（或者更大），但不会影响有效数的精度，毕竟我们没法弥补被舍弃位置本可以是 1 的情况。

二进制 → 十进制

接下来，让我们看看当有 n 个二进制位时，它能表示多少个十进制数，以及十进制数的有效位的情况。

整数部分

二进制的不同位数，能表示的最大十进制数。如下：

二进制	十进制最大数	十进制数的范围
1	2¹ - 1 = 1	< 1e1
11	2² - 1 = 3	< 1e1
111	2³ - 1 = 7	< 1e1
1111	2⁴ - 1 = 15	< 1e1 < 1e2
11111	2⁵ - 1 = 31	< 1e2
111111	2⁶ - 1 = 63	< 1e2
1111111	2⁷ - 1 = 127	< 1e2 < 1e3
11111111	2⁸ - 1 = 255	< 1e3
111111111	2⁹ - 1 = 511	< 1e3
1111111111	2¹⁰ - 1 = 1023	< 1e3 < 1e4
11111111111	2¹¹ - 1 = 2047	< 1e4
111111111111	2¹² - 1 = 4095	< 1e4
1111111111111	2¹³ - 1 = 8191	< 1e4
11111111111111	2¹⁴ - 1 = 16383	< 1e4 < 1e5
111111111111111	2¹⁵ - 1 = 32767	< 1e5
1111111111111111	2¹⁶ - 1 = 65535	< 1e5
11111111111111111	2¹⁷ - 1 = 131071	< 1e5 < 1e6

从上表可以看出，二进制的 n 个有效位可以表示十进制的 m 个有效位，用公式表示就是：

10^m-1 < 2ⁿ - 1 < 10^m，即 (m-1) < lg(2ⁿ - 1) < m

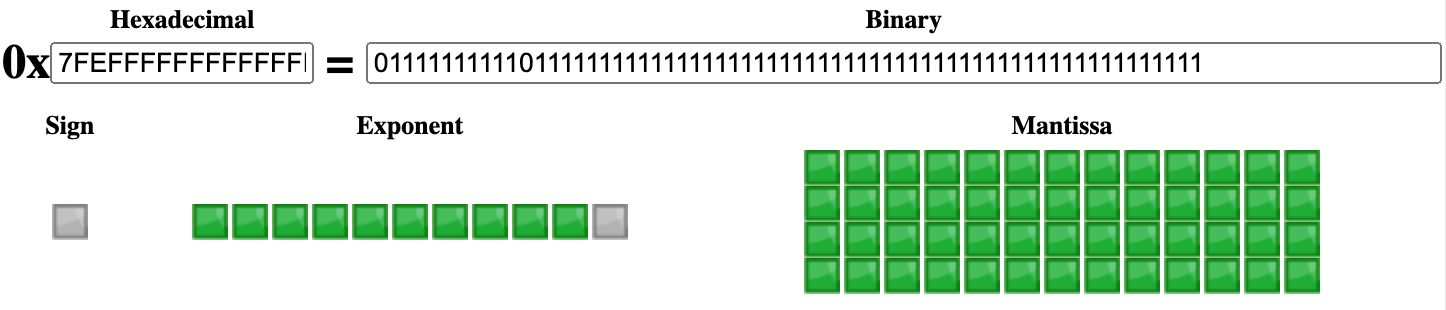
所以，在 IEEE 754 binary64 里，当 53 个有效位均为整数部分时，lg(2⁵³-1) < 16，即它能表示的十进制将最多有 16 个有效数字。

2 ** 53 - 1; // 9007199254740991 ≈ 9e15 < 1e16
Math.log10(2 ** 53 - 1); // 15.954589770191003 < 16

小数部分

二进制的不同位数，能表示的十进制数列的差值。如下：

二进制	十进制差值	差值的范围
0.1	2^-1 = 0.5 = 5e-1	> 0.1 = 1e-1
0.01	2^-2 = 0.25 = 2.5e-1	> 0.1 = 1e-1
0.001	2^-3 = 0.125 = 1.25e-1	> 0.1 = 1e-1
0.0001	2^-4 = 0.0625 = 6.25e-2	> 0.01 = 1e-2
0.00001	2^-5 = 0.03125 = 3.125e-2	> 0.01 = 1e-2
0.000001	2^-6 = 0.015625 = 1.5625e-2	> 0.01 = 1e-2
0.0000001	2^-7 = 0.0078125 = 7.8125e-3	> 0.001 = 1e-3
0.00000001	2^-8 = 0.00390625 = 3.90625e-3	> 0.001 = 1e-3
0.000000001	2^-9 = 0.001953125 = 1.953125e-3	> 0.001 = 1e-3
0.0000000001	2^-10 = 0.0009765625 = 9.765625e-4	> 0.0001 = 1e-4

从上表可以看出，二进制的 n 个有效位可以表示的十进制数列的差值的取值范围 10^-m < 2^-n，也就是说至少需要十进制的 m 个有效位。

最多需要几个呢？答案是 n 个。因为差值的小数点后有几位，能表示的十进制数列的有效数字最多就有几位。

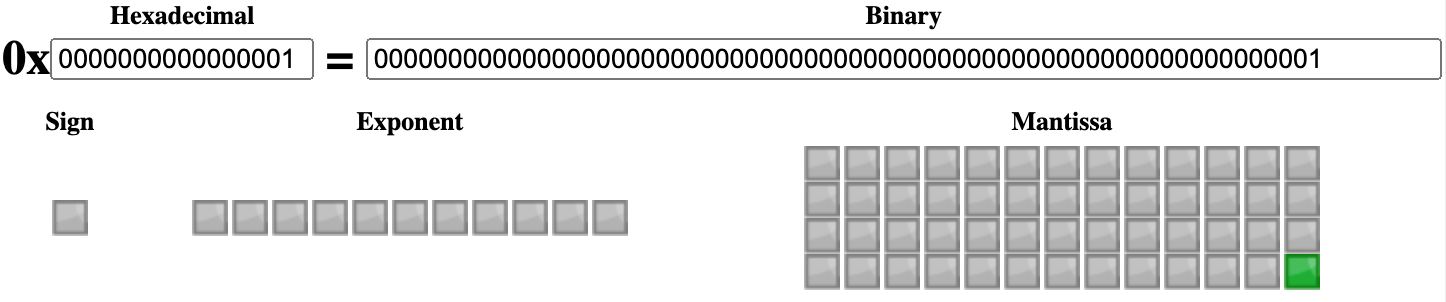
所以，在 IEEE 754 binary64 里，当 53 个有效位均为小数部分时，2^-53 ≈ -1.11e-16 > 10^-16，即它能表示的十进制小数最少要有 16 个有效数字。

2 ** -53; // 1.1102230246251565e-16

而“不连续”的小数，需要再多 1 位有效数字来进行四舍五入，故小数部分需要 17 个有效数字。

总结

本部分虽然篇幅较长，但其实就解释了一句话，就是：读内存中的 IEEE 754 binary64 数值时，只要十进制的有效数字是 17 个就能保证“内存里存啥就显示啥”。用代码表述就是 toPrecision(17) 能显示出内存中的真实值，而 toPrecision(16) 能让小数“看起来”是对的。

Number(0.1); // 0.1
Number(0.1).toPrecision(16); // '0.1000000000000000'  = 0.1
Number(0.1).toPrecision(17); // '0.10000000000000001' > 0.1

Number(0.2); // 0.2
Number(0.2).toPrecision(16); // '0.2000000000000000' = 0.2
Number(0.2).toPrecision(17); // '0.20000000000000001' > 0.2

Number(1.005); // 1.005
Number(1.005).toPrecision(16); // '1.005000000000000' = 1.005
Number(1.005).toPrecision(17); // '1.0049999999999999' < 1.005

IEEE 754 binary64 里的 53 位有效数精度能提供十进制数的 15 到 17 个有效数精度。

整数部分，有效位最多 16 位。(2⁵³-1 ≈ 9*10¹⁵) < 10¹⁶
小数部分，有效位最少 16 位，保险 17 位。10^-16 < (2^-53 ≈ 1.11e-16)

anjia commented 2 years ago

三. Number 的字面量表示

十进制 Decimal
二进制 Binary
八进制 Octal
十六进制 Hexadecimal

十进制 Decimal

常规数字。如下：

10;
1024;
9007199254740991;

当以 0 开头时，需要注意：若数字有 ≥8 的，就默认是十进制的；但如果数字全是<8 的，则会被当成八进制来解析。如下：

0888; // 888
0775; // 509，会被当成八进制

科学记数法的形式，也称指数字面量。格式是beN，其中 b 是尾数（可以是整数或浮点数），字符e/E表示分隔符或指数指示符，N 是指数（有符号的整数）。如下：

1e1; // 10
1e-3; // 0.001
5e-324; // 5e-324
9e15; // 9000000000000000
1.7976931348623157e+308; // 1.7976931348623157e+308
2.220446049250313e-16; // 2.220446049250313e-16

二进制 Binary

字面量以 0b 或者 0B 开头，这是 ECMAScript 2015 中的新语法。如下：

0b10000111; // 135
0b11111111110; // 2046
0b10000000000; // 1024
0b01111111111; // 1023
0b10000110011; // 1075

如果 0b/0B 后面的值不是 0 和 1，会报语法错误：

0b002001111; // Uncaught SyntaxError: Invalid or unexpected token

八进制 Octal

字面量以 0o 或者 0O 开头，这是 ECMAScript 2015 中的新语法。如下：

0o755; // 493
0o644; // 420

再就是前面“十进制”里提到的，以 0 开头的情况。即便“看起来”是十进制的数字，但如果它们都 <8（即在 0\~7 之间）是会被当成八进制来解析的。如下：

0755; // 493
0775; // 509

若 0o/0O 后面的值不是 0\~7，会报语法错误：

0b6339; // Uncaught SyntaxError: Invalid or unexpected token

十六进制 Hexadecimal

字面量以 0x 或者 0X 开头，后跟 0\~F。如下：

0x0010; // 16
0x7fe; // 2046
0xffff; // 65535

若 0x/0X 后面的值不是 0\~F，会报语法错误：

0x99EFG; // Uncaught SyntaxError: Invalid or unexpected token

小结

这节内容比较直观，大约就是所见即所得。对我们的启示就是：

在写进制的时候，前缀 0b/0o/0x 最好不要省略
若是接口返回来的十进制数据，如有必要，保险起见可以手动处理下开头的 0

最后简单提下，Number 类型的字面量如果都在后面加个字符 n 就是 BigInt 类型的了。如下：

755n;
9007199254740992n;
0b11111111110n; // 2046n
0o7556643555n; // 1035683693n
0xffffeeeaaan; // 1099510508202n

唯一不同的就是在 BigInt 里 0755n 不会被当成八进制，因为前缀 o/O 不能省。如下：

0755n; // Uncaught SyntaxError: Invalid or unexpected token
0o755n; //493n

主要参考

https://developer.mozilla.org/en-US/docs/Web/JavaScript/Reference/Lexical_grammar#numeric_literals

anjia commented 2 years ago

四. 如何理解 Number 里的 8 个常量？

Number 对象有 8 个静态属性，分别是：

常量	说明
`Number.MAX_VALUE` `Number.MIN_VALUE`	能表示的最大正数能表示的最小正数（最接近 0 的正数）
`Number.MAX_SAFE_INTEGER` `Number.MIN_SAFE_INTEGER`	最大安全整数，+(2⁵³ - 1) 最小安全整数，-(2⁵³ - 1)
`Number.EPSILON`	能表示的数字之间的最小间隔
`Number.NEGATIVE_INFINITY` `Number.POSITIVE_INFINITY`	正负无穷大（特殊值）上溢时返回
`Number.NaN`	Not a Number（特殊值）

它们的值分别是：

Number.MAX_VALUE; // 1.7976931348623157e+308
Number.MIN_VALUE; // 5e-324

Number.MAX_SAFE_INTEGER; //  9007199254740991 = 2**53-1
Number.MIN_SAFE_INTEGER; // -9007199254740991

Number.EPSILON; // 2.220446049250313e-16 = 2**-52

Number.POSITIVE_INFINITY; // Infinity
Number.NEGATIVE_INFINITY; // -Infinity

Number.NaN; // NaN

那么，结合《Number 在内存中的存储方式》，如何理解它们的含义和值呢？

符号位，1 位，0 正 1 负

指数，11 位，实际范围是从 -1022 到 +1023

有效数， 53 位，包括 1 个默认前导位 + 52 个显式存储位

IEEE 754 binary64 （双精度浮点数）里的指数，当它是“全 0”和“全 1”的时候是为特殊数字保留的，对此已在《浮点数的指数编码》里介绍过了，这里便不再赘述，就直接用结论了。

	有效位“全 0”	有效位非“全 0”
指数“全 0”	表示 ±`0`	表示次正规数，此时： - 有效位的默认前导位由 1 变 0 - 指数按最小指数值来解释，即 -1022
指数“全 1”	表示 ±`Infinity`	表示 `NaN`

MAX_VALUE 和 MIN_VALUE

_MAXVALUE

最大正数 MAX_VALUE 应该是：正数即符号位为 0，11 位指数是“全 1-1”，52 位有效数是“全 1”。如下：

MAX_VALUE 的 IEEE 754 binary64 存储为：0x7FEFFFFFFFFFFFFF

真实值就是：(-1)⁰ * 1.11...11₍₂₎ * 2^2046-1023

= 1.11...11₍₂₎ * 2¹⁰²³
= 111...11₍₂₎ * 2^1023-52
= 111...11₍₂₎ * 2⁹⁷¹
= (2⁵³ - 1) * 2⁹⁷¹
= 1.7976931348623157e+308
≈ 1.8e+308

0b11111111110; // 2046
(2**53 - 1) * 2**971; // 1.7976931348623157e+308
Number.MAX_VALUE; // 1.7976931348623157e+308
Number.MAX_VALUE === (2**53 - 1) * 2**971; // true

_MINVALUE

最小正数 MIN_VALUE 应该是：正数即符号位为 0，11 位指数是“全 0”，52 位有效数是“全 0+1”。此时即为次正规数，如下：

MIN_VALUE 的 IEEE 754 binary64 存储为：0x0000000000000001

真实值就是：(-1)⁰ * 0.00...01₍₂₎ * 2^-1022

= 1 * 1₍₂₎ * 2^-1022-52
= 2^-1074
= 5e-324

2**-1074; // 5e-324
Number(2**-1074).toPrecision(70); // '4.940656458412465441765687928682213723650598026143247644255856825006755e-324'
Number.MIN_VALUE; // 5e-324
Number.MIN_VALUE === 2**-1074; // true

MAX_SAFE_INTEGER 和 MIN_SAFE_INTEGER

在介绍最大安全整数和最小安全整数之前，我们先来认识下什么是“安全整数”。

The idea of a safe integer is about how mathematical integers are represented in JavaScript.
In the range (−2⁵³, 2⁵³) (excluding the lower and upper bounds), JavaScript integers are safe: there is a one-to-one mapping between mathematical integers and their representations in JavaScript.

大意是：安全整数是形容数学概念上的一个整数在 JavaScript 里的表示方式。如果说一个整数是安全的，就意味着它能在 JavaScript 中被唯一地表示。

那么，如何理解“被唯一”地表示呢？来看个例子。

当 IEEE 754 binary64 的 53 个有效位全是 1 且都处于整数位置时，即实际指数值是 52，偏正指数值是 52+1023 = 1075 = 10000110011₍₂₎，此时的内存表示如下：

真实值就是：(-1)⁰ * 1.11...11₍₂₎ * 2⁵²

= 1.11...11₍₂₎ * 2⁵²
= 111...11₍₂₎
= 2⁵³ - 1
= 9007199254740991

当它加 1 时，值会变成 2⁵³ = 1000...00₍₂₎ = 1.00...000 * 2⁵³。注意，末位的 0 之所以被删，是因为内存里的 IEEE 754 binary64 格式的有效位只有 53 个（包括默认的前导位 1），所以需要裁切精度（ 0 舍 1 入）。

当再加 1 时，值会变成 2⁵³ + 1 = 1000...01₍₂₎ = 1.00...001 * 2⁵³ ≈ 1.00...01 * 2⁵³。

为了方便阅读，我们用表格的形式来描述。十进制那列是从 2⁵³ - 1 即 9007199254740991 开始的，每行的值依次加 1。如下：

十进制	二进制	二进制的科学记数法	IEEE 754 binary64
9007199254740991 即 2⁵³ - 1	111...11	1.11...11₍₂₎ * 2⁵²	1.11...11₍₂₎ * 2⁵²
9007199254740992 即 2⁵³	1000...00	1.000...00₍₂₎ * 2⁵³	1.00...00₍₂₎ * 2⁵³
9007199254740993	1000...01	1.000...01₍₂₎ * 2⁵³	1.00...01₍₂₎ * 2⁵³
9007199254740994	1000...10	1.000...10₍₂₎ * 2⁵³	1.00...01₍₂₎ * 2⁵³
9007199254740995	1000...11	1.000...11₍₂₎ * 2⁵³	1.00...10₍₂₎ * 2⁵³
9007199254740996	100...100	1.00...100₍₂₎ * 2⁵³	1.00...10₍₂₎ * 2⁵³
9007199254740997	100...101	1.00...101₍₂₎ * 2⁵³	1.00...11₍₂₎ * 2⁵³
9007199254740998	100...110	1.00...110₍₂₎ * 2⁵³	1.00...11₍₂₎ * 2⁵³
...

对于精度裁切，上表用的是四舍五入（即 0 舍 1 入）的舍入方式。如果是用向 0 舍入的方式（即直接截断），那么相互重叠的数字会有一点点出入。

我们可以很直观地看到，当二进制有效数的位数大于 53 位时，就得 0 舍 1 入地舍弃最后一位，这会导致值不同的两个数字会有相同的 IEEE 754 binary64 表示。这，就是没有“被唯一”地表示。

当指数是 53 时，是 2 个整数共用一个内存存储，因为会舍去末位的 53-52 = 1 位

当指数是 54 时，是 4 个整数共用一个共存储存，因为会舍去末位的 54-52 = 2 位

当指数是 55 时，是 8 个整数共用一个共存储存，因为会舍去末位的 55-52 = 3 位

当指数是 56 时，是 16 个整数共用一个共存储存，因为会舍去末位的 56-52 = 4 位

...

JavaScript 里的安全整数的范围是 [-(2⁵³-1), +(2⁵³-1)]，没有包含边界 ±2⁵³。虽然 2⁵³ 在内存中是能被唯一表示的，但是考虑到如果是用直接截断的方式，它是会和 2⁵³+1 重叠的，所以在 JavaScript 中，一旦精度被四舍五入了，也会被视为是不安全的。如下：

Number.isSafeInteger(2**53 - 1); // true
Number.isSafeInteger(2**53); // false
Number.isSafeInteger(2**53 + 1); // false

在 JavaScript 中，说一个整数是安全的，就意味着它能唯一地表示一个数学意义上的整数，且在存储时没有被舍弃精度。

https://2ality.com/2013/10/safe-integers.html

_MAX_SAFEINTEGER

最大安全整数 MAX_SAFE_INTEGER 应该是：正数即符号位为 0，指数的实际值是 52（即内存值为 52+1023 = 1075 = 10000110011₍₂₎ ），52 位有效数是“全 1”。如下：

MAX_SAFE_INTEGER 的 IEEE 754 binary64 存储：0x433FFFFFFFFFFFFF

真实值就是：(-1)⁰ * 1.11...11₍₂₎ * 2⁵²

= 1.11...11₍₂₎ * 2⁵²
= 111...11₍₂₎
= 2⁵³ - 1
= 9007199254740991

0b10000110011; // 1075
2 ** 53 - 1; // 9007199254740991
Number.MAX_SAFE_INTEGER; // 9007199254740991
Number.MAX_SAFE_INTEGER === 2 ** 53 - 1; // true

_MIN_SAFEINTEGER

最小安全整数 MIN_SAFE_INTEGER 除了符号和最大安全整数 MAX_SAFE_INTEGER 不同之外，其余都一样，即：负数即符号位为 1，指数的实际值是 52（即内存值为 52+1023 = 1075 = 10000110011₍₂₎），52 位有效数是“全 1”。如下：

MIN_SAFE_INTEGER 的 IEEE 754 binary64 存储：0xC33FFFFFFFFFFFFF

真实值就是：(-1)¹ * 1.11...11₍₂₎ * 2⁵²

= -1.11...11₍₂₎ * 2⁵²
= -111...11₍₂₎
= - (2⁵³ - 1)
= -9007199254740991

0b10000110011; // 1075
2 ** 53 - 1; // 9007199254740991
Number.MIN_SAFE_INTEGER; // -9007199254740991
Number.MIN_SAFE_INTEGER === -(2 ** 53 - 1); // true

EPSILON

在《如何理解二进制浮点数的精度损失》里曾提到浮点数到实数的映射，如下图：

中间有覆盖不到的小断层

能表示的两个数字之间的“间隔”，就是图中的那些个“小断层”。那么，这些断层是均匀的吗？如果均匀，值是多少？如果不均匀，最小值和最大值分别是多少？

要回答这个问题，我们就得看看二进制到十进制的转换了。在《为什么 toPrecision(17) 能让内存中的数值原形毕露？》里我们是将整数部分和小数部分分开来讨论的，相关结论是：

整数部分，当有 n 个二进制有效位时，可以表示 2ⁿ 个十进制数，且它们是个等差数列，差值是 1
小数部分，当有 n 个二进制有效位时，可以表示 2ⁿ 个十进制数，且它们是个等差数列，差值是 2^-n，数列范围是 [2^-n, 1)

在真实的 IEEE 754 binary64 存储中，二进制的那 53 个有效位是可以同时有整数部分和小数部分的，如果再考虑指数，这会让每个有效位上的数字权重（即2的几次方）变成流动的。所以显然，两个能表示的数之间的“间隔”是不均匀的。

那间隔的最小值和最大值分别是多少？

假设现在有 4 个二进制有效位，其中包括 1 个默认前导位和 3 个显式存储位。我们看看在这种情况下，二进制到十进制是一个什么样的对应关系。如下：

格式	二进制	十进制	间隔值
0.xxx	0.000 0.001 0.010 0.011 0.100 0.101 0.110 0.111	0 0.125 0.25 0.375 0.5 0.625 0.75 0.875	0.125 = 2^-3
1.xxx	1.000 1.001 1.010 1.011 1.100 1.101 1.110 1.111	1 1.125 1.25 1.375 1.5 1.625 1.75 1.875	0.125 = 2^-3
1x.xx	10.00 10.01 10.10 10.11 11.00 11.01 11.10 11.11	2 2.25 2.5 2.75 3 3.25 3.5 3.75	0.25 = 2^-2
1xx.x	100.0 100.1 101.0 101.1 110.0 110.1 111.0 111.1	4 4.5 5 5.5 6 6.5 7 7.5	0.5 = 2^-1
1xxx	1000 1001 1010 1011 1100 1101 1110 1111	8 9 10 11 12 13 14 15	1 = 2⁰

同理，当我们有 53 个二进制有效位时（1 个默认前导位 + 52 个显式位），从 0 \~ 1 \~ 2¹ \~ 2² \~ 2³ \~ 2⁴ \~ ... \~ (2⁵³ - 1) 之间，每段都是连续的等差数列，只是差值不同而已。其中，最小差值是 2^-52，最大差值是 2⁰ = 1。

之所以只考虑了次正规数和 0 ≤ 指数实际值 ≤ 52 的情况，是因为当指数过大或者过小时，能表示的数字就不是线性连续的了。感兴趣的小伙伴们，可以自行推导下。

在数轴上，二进制和十进制的逻辑类似

综上，最小间隔 EPSILON 就是能表示的等差数列的最小差值，即 2^-52 = 2.220446049250313e-16

2**-52; // 2.220446049250313e-16
Number.EPSILON; // 2.220446049250313e-16
Number.EPSILON === 2**-52; // true

POSITIVE_INFINITY 和 NEGATIVE_INFINITY

这俩就是指数位“全 1”的特殊情况（之一）：指数位是“全 1”，有效数位是“全 0”。如下图：

infinity 的 IEEE 754 binary64 存储：0x7FF0000000000000

-infinity 的 IEEE 754 binary64 存储：0xFFF0000000000000

Number.POSITIVE_INFINITY === Infinity; // true
Number.NEGATIVE_INFINITY === -Infinity; // true

NaN

NaN 也是指数位“全 1”的特殊情况（之一）：指数位是“全 1”，只要有效数位不是“全0”的都是 NaN（忽略符号位）。如下图：

从 0x7FF0000000000001 \~ 0x7FFFFFFFFFFFFFFF 都是 NaN

±0

0 有两种表示方式：-0 和 +0（0 是 +0 的别名）。在实际开发中，这几乎没啥影响。但需要注意一点，就是当 0 是被除数的时候，会有不同：

33 / 0; // Infinity
33 / -0; // -Infinity
-0 === 0; // 虽然是 true

+0 的 IEEE 754 binary64 存储

-0 的 IEEE 754 binary64 存储

小结

本节介绍了 Number 对象里的 8 个静态属性：

能表示的最大正数和最小正数
- Number.MAX_VALUE 即最大正“正规数”
- Number.MIN_VALUE 即最小正“次正规数”
能表示的最大安全整数和最小安全整数
- 安全整数：内存存储可唯一对应到一个整数 + 没有精度裁切
- Number.MAX_SAFE_INTEGER
- Number.MIN_SAFE_INTEGER
能表示的数字之间的间隔
- 浮点数→实数：有间隔，且间隔不均匀
- 在线性增长中，是 n 段等差数列
  - 最小间隔/差值是 Number.EPSILON
  - 最大间隔/差值是 1
- 在指数增长中
几个特殊值：NaN, ±Infinity, ±0
- Number.NaN
- Number.NEGATIVE_INFINITY
- Number.POSITIVE_INFINITY

zzz6519003 commented 2 years ago

数学归纳法咋推出的？

anjia commented 2 years ago

数学归纳法咋推出的？

就是依次总结下规律，来推出当 n+1 时的情况

anjia / blog

关于 Number 需要知道的事 #88

目录

87

二. 为什么 `toPrecision(17)` 能让内存中的数值原形毕露？

当有效位逐个增加

纯整数

纯小数

小结

二进制 → 十进制

整数部分

小数部分

总结

三. Number 的字面量表示

十进制 Decimal

二进制 Binary

八进制 Octal

十六进制 Hexadecimal

小结

主要参考

四. 如何理解 Number 里的 8 个常量？

MAX_VALUE 和 MIN_VALUE

_MAXVALUE

_MINVALUE

MAX_SAFE_INTEGER 和 MIN_SAFE_INTEGER

_MAX_SAFEINTEGER

_MIN_SAFEINTEGER

EPSILON

POSITIVE_INFINITY 和 NEGATIVE_INFINITY

NaN

±0

小结

anjia / blog

关于 Number 需要知道的事 #88

目录

87

二. 为什么 toPrecision(17) 能让内存中的数值原形毕露？

当有效位逐个增加

纯整数

纯小数

小结

二进制 → 十进制

整数部分

小数部分

总结

三. Number 的字面量表示

十进制 Decimal

二进制 Binary

八进制 Octal

十六进制 Hexadecimal

小结

主要参考

四. 如何理解 Number 里的 8 个常量？

MAX_VALUE 和 MIN_VALUE

_MAXVALUE

_MINVALUE

MAX_SAFE_INTEGER 和 MIN_SAFE_INTEGER

_MAX_SAFEINTEGER

_MIN_SAFEINTEGER

EPSILON

POSITIVE_INFINITY 和 NEGATIVE_INFINITY

NaN

±0

小结

二. 为什么 `toPrecision(17)` 能让内存中的数值原形毕露？