anjia
commented
2 years ago 1. 复杂度分析
复杂度也叫渐进复杂度，包括时间复杂度和空间复杂度。
- 时间复杂度（渐进时间复杂度）表示算法的执行时间与数据规模之间的增长关系。
- 空间复杂度（渐进空间复杂度）表示算法的存储空间与数据规模之间的增长关系。
asymptotic time complexity \~ 执行时间 \~ 更快
asymptotic space complexity \~ 存储空间 \~ 更省
大 O 时间复杂度表示法
大 O 复杂度表示方法只是表示一种变化趋势。
T(n) = O(f(n))，n 表示数据规模的大小
T(n)所有代码的执行时间f(n)每行代码的执行次数之和- 大 O 表示
T(n)和f(n)成正比- 即代码的执行时间和代码的执行次数成正比
假设每行代码的执行时间都一样，为 unit_time。eg.
T(n) = (2n+2) * unit_time = O(2n+2) = O(n)
T(n) = (2n2 + 2n + 3) * unit_time = O(2n2 + 2n + 3) = O(n2)
大 O 时间复杂度实际上并不表示代码真正的执行时间，而是表示代码执行时间随数据规模增长的变化趋势。通常我们会忽略掉公式中的常量、低阶、系数，只需要记录一个最大阶的量级就可以了。
当 n 很大时，公式中的低阶/常量/系数并不左右增长趋势，故都可忽略。
复杂度量级
几种常见的复杂度量级（从低阶到高阶）如下：
| 分类 | 复杂度量级 | 大 O 表示 |
|---|---|---|
| 多项式量级 | 常量阶 | O(1) |
| 对数阶 | O(logn) |
|
| 线性阶 | O(n) |
|
| 线性对数阶 | O(nlogn) |
|
| 平方阶 立方阶 k 次方阶 |
O(n2)O(n3)O(nk) |
|
| 非多项式量级 | 指数阶 | O(2n) |
| 阶乘阶 | O(n!) |
说明：
O(1)只是常量级时间复杂度的一种表示方法，并不是表示只执行了一行代码- 一般情况下，只要算法中不存在循环/递归语句，即使有成千上万行的代码，其时间复杂度也是
Ο(1) - 大 O 这种复杂度表示方法只是表示一种变化趋势
- 一般情况下，只要算法中不存在循环/递归语句，即使有成千上万行的代码，其时间复杂度也是
- 对数阶
O(logn)和线性对数阶O(nlogn)- 不论对数的底是几都记为
O(logn)，因为换底公式可以提取任意常量 - eg. log3n = log32 * log2n
O(nlogn)即一段时间复杂度为O(logn)的代码循环了 n 遍
- 不论对数的底是几都记为
- 非多项式量级的算法问题也叫 NP 问题
- NP, Non-Deterministic Polynomial, 非确定多项式
- 当数据规模 n 越来越大时，其执行时间会急剧增加/无限增长
空间复杂度
常见的空间复杂度有 O(1), O(n), O(n2)
像
O(logn),O(nlogn)这样的对数阶复杂度平时都用不到
- 静态数组的长度
- 递归的深度（栈上消耗的空间）
- 动态new的空间（堆上消耗的空间）
看几个例子
对于时间复杂度：
- 只需关注循环执行次数最多的一段代码
- 这段核心代码执行次数的 n 的量级，就是整段要分析代码的时间复杂度
- 总的时间复杂度就等于量级最大的那段代码的时间复杂度（加法法则）
- 嵌套代码的复杂度等于嵌套内外代码复杂度的乘积（乘法法则/嵌套循环）
有的代码的复杂度是由多个数据规模来决定的
eg. O(m+n), O(m*n)
function add(n) {
let sum = 0;
for (let i = 1; i <= n; i++) {
sum += i;
}
return sum;
}
// 时间复杂度 T(n) = (1+2n) * unit_time = O(1+2n) = O(n)
// 空间复杂度 O(1)function add(n) {
let sum = 0;
for (let i = 1; i <= n; i++) {
for (let j = 1; j <= n; j++)
sum += i * j;
}
return sum;
}
// 时间复杂度 T(n) = (1+n+2n^2) * unit_time = O(1+n+2n^2) = O(n^2)
// 空间复杂度 O(1)let count = 0;
let i = 1;
while (i < n) {
count++;
i = i * 2;
}
// 时间复杂度 T(n) = O(log(n))20, 21, 22, 23 ... 2k ... 2x = n
x = log2n
NE-SmallTown
zzz6519003
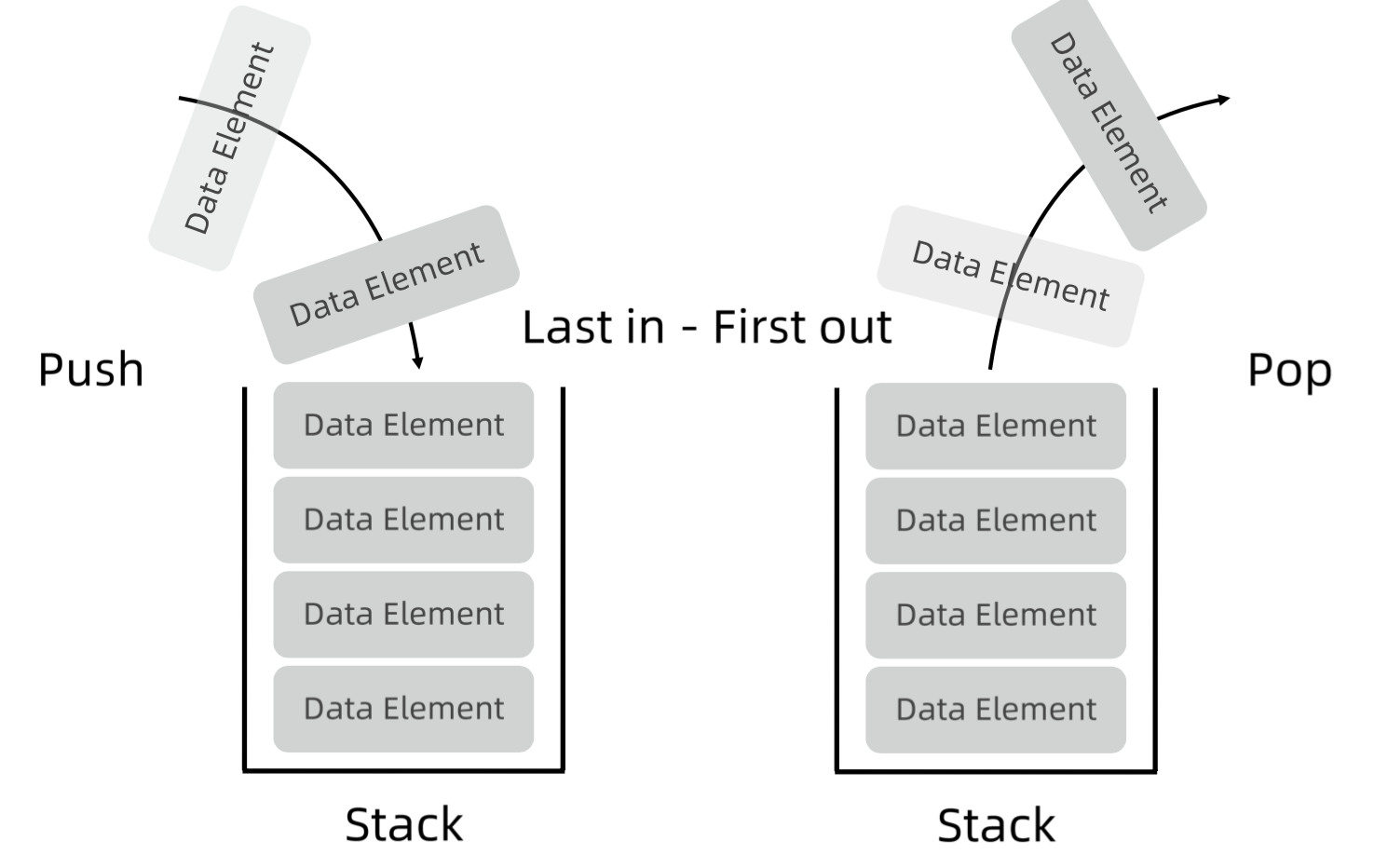
目录
O(1),O(logn),O(n),O(nlogn),O(n2)/O(n3)/O(nk)O(2n),O(n!)