Hi, indeed using Dynp(model="l2") results in a O(log(T^3)) complexity where T is the number of samples. Using precomputed cumsum vectors will definitely make it faster.
The fastest way to detect mean-shifts is to use KernelCPD(kernel="linear"). It follows this article and is coded in C. The complexity is quadratic in number of operations and linear in memory.
See here for a comparison between the Python implementation and the C implementation.
 This result suggests that some other property of ruptures (not the l2 cost function) is the source of the slowdown. (maybe the storage of previously computed splits in the LRU cache?)
This result suggests that some other property of ruptures (not the l2 cost function) is the source of the slowdown. (maybe the storage of previously computed splits in the LRU cache?) This is using
This is using
related to benchmarks #231 I recently computed timings for ruptures.Binseg using the l2 model (normal change in mean, square loss) for univariate data, https://github.com/tdhock/binseg-model-selection#22-mar-2022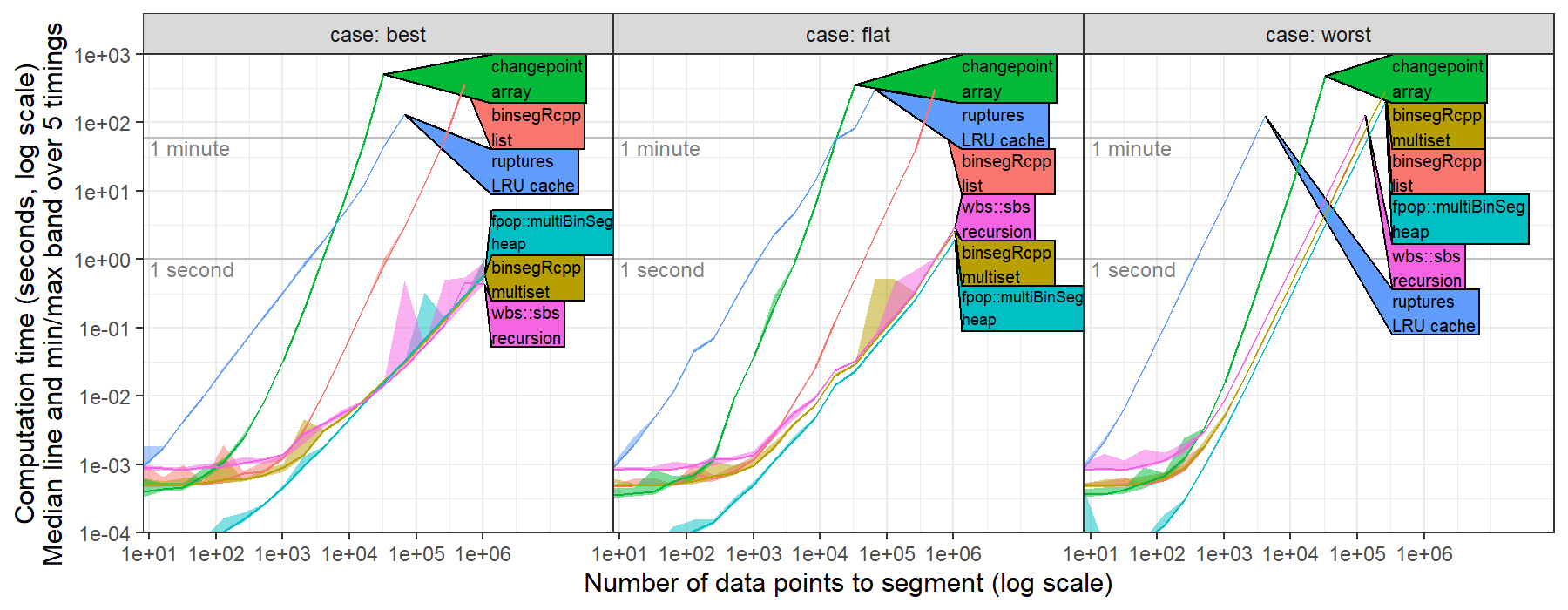 For worst case data, ruptures shows the expected/optimal quadratic time complexity.
For best case data, ruptures was slower than the expected/optimal log-linear time complexity.
This is probably because the time complexity of CostL2.error(start,end) is linear in number of data, O(end-start).
Could probably be fixed by computing cumsum vectors in fit method, then using them to implement a constant O(1) time error method.
For worst case data, ruptures shows the expected/optimal quadratic time complexity.
For best case data, ruptures was slower than the expected/optimal log-linear time complexity.
This is probably because the time complexity of CostL2.error(start,end) is linear in number of data, O(end-start).
Could probably be fixed by computing cumsum vectors in fit method, then using them to implement a constant O(1) time error method.