Need a base grid class (i.e. not staggered)

[ggorman]

Currently we can only use staggered grids. Also need to support the simple non-staggered case.

[ggorman]

Use the 3D acoustic equation with a 25 point stencil as in http://people.csail.mit.edu/yuantang/pochoir_hotPar11.pdf as a test case.

@mlange05 @NathanYukai - this example should be amenable to diamond.

[tj-sun]

For the 3D wave case in the pochoir paper, I suppose we need to model u_x, u_y, u_z? Any books or papers you recommend about the PDE? The ones I found seems to be using pressure and bulk modulus.

[ggorman]

Implementation of a 3D wave equation to use as a reference:

http://supertech.csail.mit.edu/papers/pochoir_hotpar11.pdf

[navjotk]

In the linked paper, Figure 1 describes the Pochoir code to solve the 3D wave equation. Line 11 of this code reads: pa(t+1,z,y,x) = 2*pa(t,z,y,x) - pa(t+1,z,y,x)+ vsq[z*Nxy + y*Nx + x]*div;. Referring to this paper cited in the Pochoir paper, we see a similar equation, albeit with a small difference: the second term on the right side is referencing the index t-1 instead of t+1 as in the Pochoir paper.

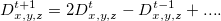
Unless we have misunderstood the relation between the two equations, one of them is likely to be an error. Logically, since pa(t+1,z,y,x) is the term being initialised in this line of code, it does not belong on the right side. Rather, pa(t-1, z, y, x) which would have already been calculated by this point in the program execution looks like it should be the correct term.

This leads us to believe that the code in the Pochoir paper is incorrect and the equation in Micikevicius, 2009 is the way to go. Could someone please confirm this observation?

[ggorman]

Hi Navjot

You could try to work out it. I have attached a 1D example which you could play with. You can see that the heart of the matter is a taylor series expansion from which you solve using a central difference scheme.

Regards Gerard

On 22 Jan 2016, at 19:25, Navjot Kukreja notifications@github.com<mailto:notifications@github.com> wrote:

In the linked paper, Figure 1 describes the Pochoir code to solve the 3D wave equation. Line 11 of this code reads: pa(t+1,z,y,x) = 2_pa(t,z,y,x) - pa(t+1,z,y,x)+ vsq[z_Nxy + y_Nx + x]_div;. Referring to thishttp://dl.acm.org/citation.cfm?id=1513905 paper cited in the Pochoir paper, we see a similar equation, albeit with a small difference: the second term on the right side is referencing the index t-1 instead of t+1 as in the Pochoir paper.

[Equation]https://camo.githubusercontent.com/bf126b915f005f136a7ebba96d9c6900b62ec5de/687474703a2f2f6d61746875726c2e636f6d2f6a363937616c642e706e67

Unless we have misunderstood the relation between the two equations, one of them is likely to be an error. Logically, since pa(t+1,z,y,x) is the term being initialised in this line of code, it does not belong on the right side. Rather, pa(t-1, z, y, x) which would have already been calculated by this point in the program execution looks like it should be the correct term.

This leads us to believe that the code in the Pochoir paper is incorrect and the equation in Micikevicius, 2009 is the way to go. Could someone please confirm this observation?

— Reply to this email directly or view it on GitHubhttps://github.com/opesci/opesci-fd/issues/43#issuecomment-174018331.

[navjotk]

Commit 38fb51b81bf3453411404e155f914d1eeeed06ac has implemented a much simplified version of the regular grid. We are currently able to generate the C code fine, for both the Staggered Grid and the Regular Grid example. However, when trying to use the built-in "execute" functionality, Staggered Grid works while our Regular Grid example gives a Segmentation Fault. We are unable to figure out what is the difference between the two calls that is causing this error. Could you please have a look @mlange05 ?

[mlange05]

@navjotk I just ran the latest simplewaveequation test from your branch and the segfault seems to originate in the second initialisation loop, where the margin value is 2 although the stencil accesses TEST[_t0][_x][_y][_z - 3]. This causes the z-index to go out of bounds causing the segfault.

[navjotk]

@mlange05 Thanks for that pointer. It was being caused by an error in the function that generates the Taylor coefficient matrix. That is fixed now in 8dd3ddbbd6258d73b389469ac51251470f7c4f65 . I tested by running the generated C code as an executable, as well as by copying the code in grid.execute to a separate file that imports the generated shared library and calls the function. It runs fine in both these cases. However, using the framework, it still generates a seg fault, although the fault seems to be after the "execute" call now (after the last changes). I am not able to find what might be causing this (different) seg fault. Some more help please?

[mlange05]

@navjotk It seems to be running fine for me as a standalone compile and through the auto-wrappers. Can you please run this in a clean checkout of the branch and tell we the exact command?

Edit: I also note travis errors due to the way we initialise some the PAPI counters, which could explain your troubles. I think this might also related to issue #62, so I'll take a look and see how we can improve this.

Another edit: Ok, I just pushed two commits to your branch. The first one deals with the current travis failures due to static/non-static PAPI variable initialisation (issue #62). After that I got exactly the kind of segfault you described, which I believe to due to our over-zealous DLL unloading. I simply removed the unload (it was never truly cross-platform anyway), which seems to fix the problem. Can you please confirm that this now works for you?

[navjotk]

Thanks for the help on this @mlange05 . This did in fact fix the problem.

Edit: Now, could I have some feedback on the code, please?

1. Generated Kernel: While it seems very similar to the kernel in the pochoir paper, the velocity term from the pochoir paper is missing here. I have tried deriving the expression from first principles and still don't see how the velocity term can be a coefficient to the stencil. The expression in the generated kernel matches my expectations as I derived on paper - assuming that the initial velocity at t=0 would be provided as an input to the model in the form of a scalar which would be expanded to the 3d matrix in x,y and z.
2. Initial condition (position) - The simpler derivations assume that the initial displacement is zero. Since this seems too restrictive for this library, we assume that the initial displacements can be seen as 3-D matrix for t=0 and the matrix coordinates x,y and z. Instead of passing the entire matrix in the form of numerical quantities, we choose to take input in the form of a function of x, y, z. This could be any function (we use sin(x+y+z) as an illustrative example). This function is then used to populate the matrix of starting positions on the grid cube representing t=0.
3. Initial condition (velocity) - The second initial condition, that of velocity, was also assumed to be zero at the starting point in the derivations we studied. This thesis derives an expression (page 8) for the initialisation of elements of the cube at t=1, which assumes that v=0 in the initial condition. We extended this expression to handle non-zero starting velocities as well. I am not sure of the validity of this approach since analytically, it involves multiplying the velocity by dt, which seems pointless in the limit of dt tending to zero. Numerically as well, I doubt that this is helping a lot given the limit of floating point accuracy. While the current version assumes that the initial velocity is provided as a scalar constant (which is later expanded to a 3D matrix in x,y,z), we are already working on a version that can take initial velocity as a function in x, y and z, similar to 2 above.

Points 1 and 3 seem related in that there might be an alternate way of taking initial velocity conditions into account that doesn't involve multiplying it by the infinitesimal dt. This might be how the velocity term ends up in the core kernel. Still not sure how that comes to be though. Could you please point us to some reading material on this maybe?

Another Edit: @mlange05 1ee1c8dd6fcdc77f84a66450c2d32bd15773e719 completes cgen integration

[navjotk]

The latest commit eada9b46c3c679ba27030cdd0ef2801f94d69c07 fixes the Travis errors (which were because of a template based code generation that was missed previously) and the deviance in the convergence values (which was because of an old bug that surfaced because of the latest changes).

As discussed with @mlange05 on the call today, this should complete the requirements for a pull request to be opened on this branch.

One of the remaining concerns with the regular grid implementation is the stability condition with respect to dt. The staggeredgrid class had a method get_time_step_limit which was calculating this. We have not implemented this functionality for the regular grid but I believe it can and should be calculated. To get some context on how this is done, I would like confirmation on whether it's the same as what is explained in section 10.3 here. Could you please help us out here @ggorman ?

[ggorman]

With respect to get_time_step_limit() - there are a lot of assumptions here. What it does is calculates Vp (the speed of the p-wave) using Vp = ((l + 2m)/r)*0.5 where l and m are the lame parameters, and r is the density:

$$v_p= \sqrt{ \frac {K+\frac{4}{3}\mu} {\rho}}= \sqrt{ \frac{\lambda+2\mu}{\rho}}$$

See https://en.wikipedia.org/wiki/P-wave for more details.

Once you have Vp you use the Courant–Friedrichs–Lewy (CFL) condition to determine the maximum time step for a given grid spacing:

$$\Delta t \sum{i=1}^n\frac{u{x_i}}{\Delta xi} \leq C\max $$ and rearrange to get $\Delta t$.

However, this is a "necessary but not sufficient" condition for numerical stability. The additional constant in the equations I believe come from: http://link.springer.com/chapter/10.1007%2F978-1-4020-8758-5_4 Need to double check.

So - writing a general function to calculate the time step is not as simple as what's currently in get_time_step_limit(). I think what we need instead is for the user to provide a callback function to calculate the time stepping.

[mlange05]

Ok, I think the timestepping callback function is an issue in it's own right and should not stop us from landing the current branch. @navjotk, do we have enough to replicate the original pochoir implementation and can we compute an error for the generated solution? If so you should go ahead and create a pull request.

[navjotk]

We could probably calculate the CFL bound internally as well as provide the option for callbacks to calculate more constrained bounds. Now that I understand this, calculating the CFL bound for the simple wave equation is quite straightforward since we are accepting the c from the equation as a scalar parameter. @mlange05: We are able to replicate the pochoir implementation, except for the differences I mentioned previously. The remaining concerns as of now:

1. Error calculation: We haven't implemented this yet. I will start on this now. Any pointers would be appreciated.
2. We are taking the wave speed (c from the DE) as a direct parameter input in the form of a scalar. This might need to be adapted to provide the velocity in the form of axial components as I see a lot of implementations doing it that way.
3. Velocity boundary condition: The implementations I have seen accept the velocity boundary condition as V(x,y,z), a function in the spatial coordinates. Our current implementation can only accept the velocity boundary condition as a constant scalar.