Initial IPM fits and data questions

Hi @kalebentley, sorry this has taken so long. The data wrangling turned out to be nontrivial; I kept encountering unanticipated wrinkles and did a lot of iterating between data cleaning and model fitting with strange results that eventually pointed back to data issues, etc. I'm working on a RMarkdown vignette, but I wanted to put some preliminary results up here for discussion ASAP.

First, let me run through the key decisions / assumptions I made in data cleaning and ask you if they make sense. The following points relate to the spawner abundance data.

In a number of cases, I had to decide whether observations (Abund.Mean) coded as NA were truly missing or were actually zeros. A typical scenario would be a naturally spawning population with broodstock removals (i.e., "hatchery" dispositions), where natural spawner abundance and/or one or more broodstock dispositions were NA in some years. In such cases, summing the natural spawners and broodstock removals to get S_obs (total returning adults) would obviously return NA. This resulted in an awful lot of missing values. The problem was most acute for Duncan Creek, where I think there were only 2 years with non-missing S_obs. To deal with this, I made some judgment calls:

NAs in hatchery dispositions (including Duncan Channel) are really zeros. I reasoned that the number of fish taken for broodstock should always be recorded, and in most cases it was.
NAs in Duncan Creek from 2004-present are really zeros. Since there is a weir, I assumed we knew the number of returning adults and where they ended up (Duncan Creek, Duncan Channel, or Duncan Hatchery) every year once monitoring started. There were no non-missing values for any disposition until 2004, so I assumed that was the start of the time series.
All other NAs in natural spawner abundance are real missing observations.

I excluded all cases with leading NAs in S_obs even when (to my surprise) there were BioData available. Missing spawner abundance in the initial 1:max_age years of a time series causes problems for model fitting because there are obviously no earlier data to constrain the process model of recruitment. Initial states are given diffuse priors, and typically the process-model information flowing backward from later data is insufficient to identify them. I gave it a shot anyway, since some populations have age- and origin-composition data starting before the spawner abundance series (but of course the compositional data don't inform the absolute scale, just relative cohort strength). The resulting fits were a disaster, to use the technical term, so I trimmed the leading NAs and things became much better-behaved.

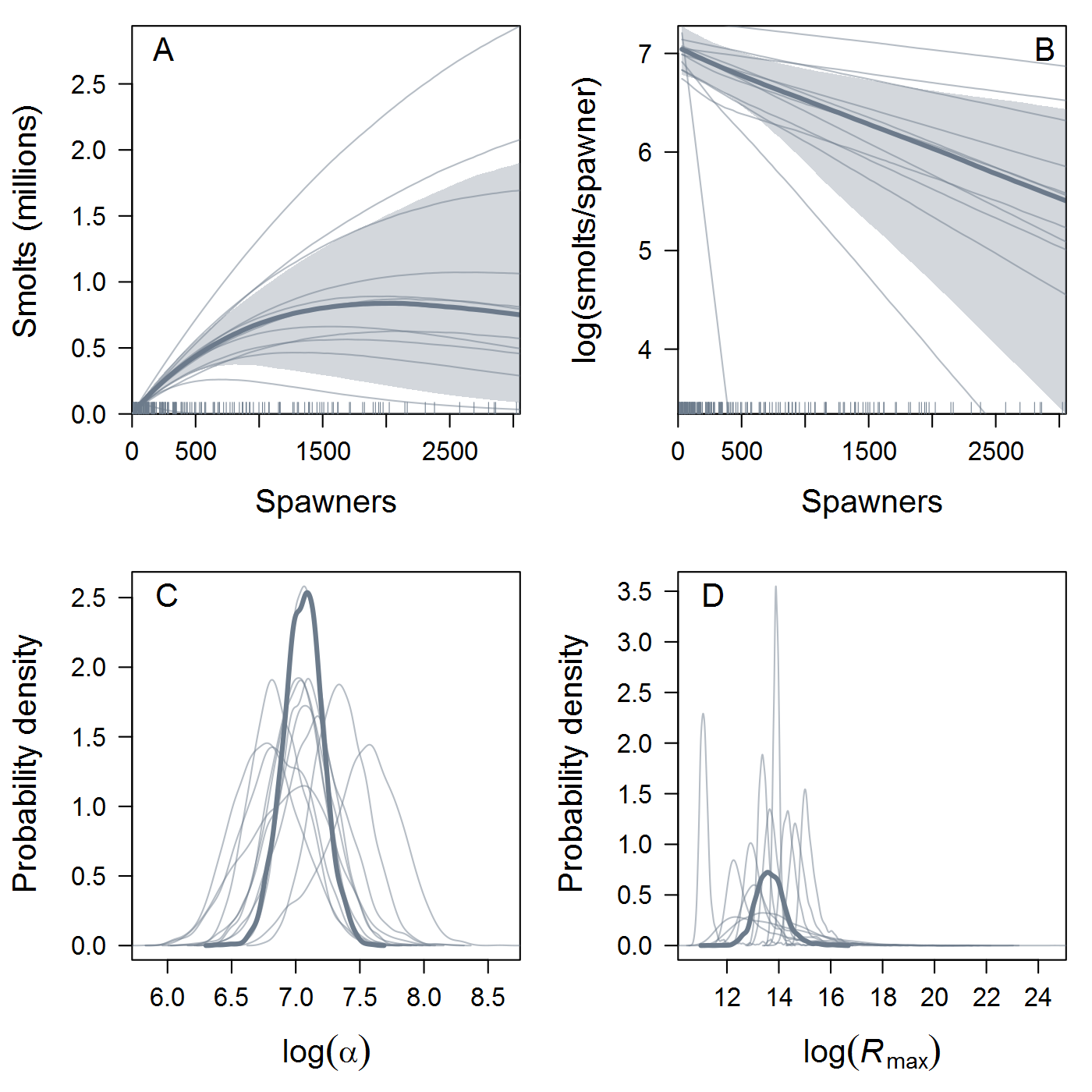
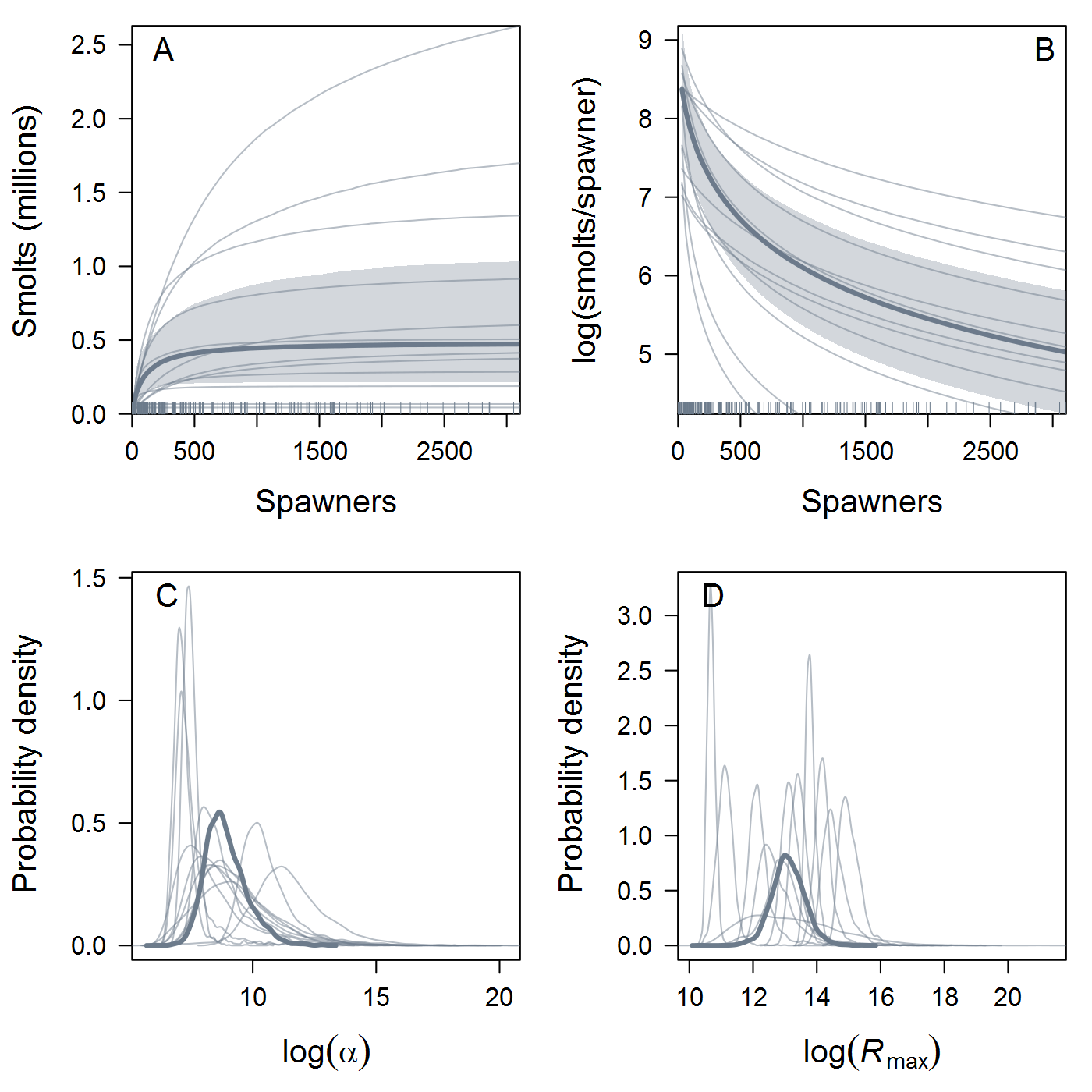
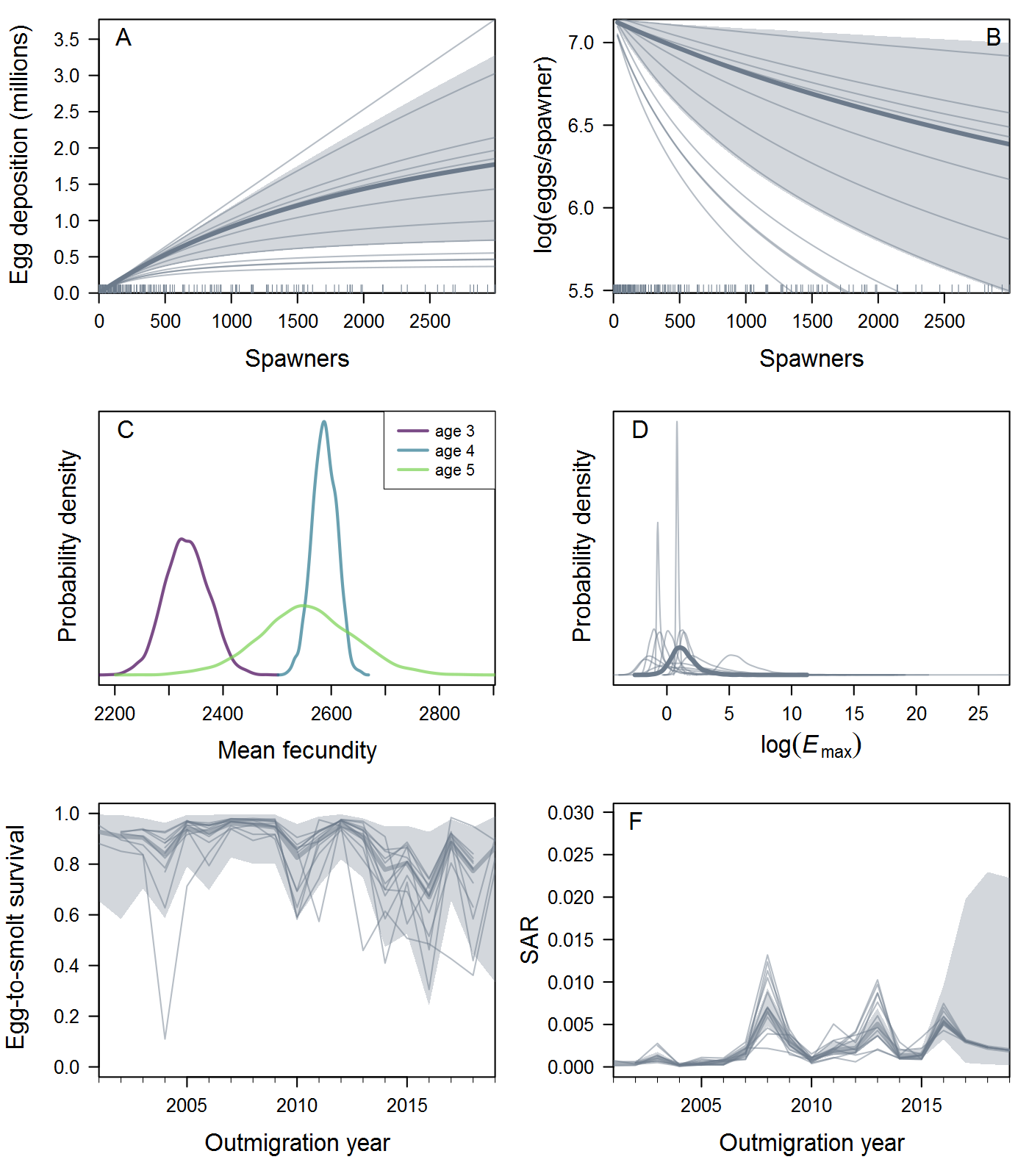
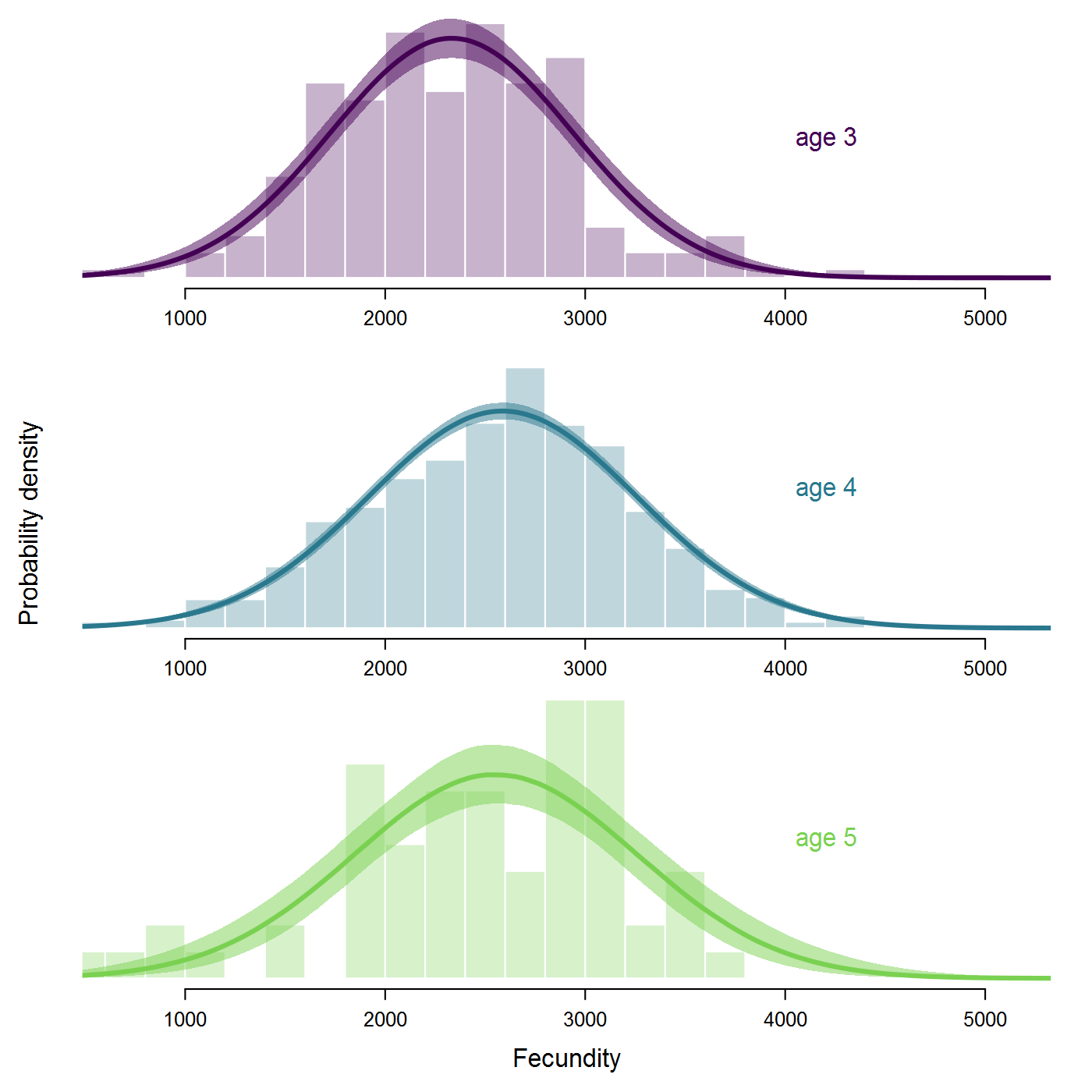
Finally, I ended up departing from the mapping of Location.Reach to pop that you proposed. I first tried your 8 populations (Population1 in the table below) but ran into computational problems (terrible mixing, lots of divergences, etc.) that weren't resolved by the usual Stan techniques. Eight is a pretty small number of groups for hierarchical modeling, so I tried a more "splitty" grouping with 12 populations (Population2) and got much more stable and sensible results. This could be a case of Gelman's folk theorem, or it could just be luck (Stein's paradox and all that). Either way, the results shown below are based on the 12-population data.

Strata	Location.Reach	Population1	Population2
Coastal	Grays_CJ	CJ	Grays_CJ
Coastal	Grays_MS	Grays	Grays_MS
Coastal	Grays_WF	Grays	Grays_WF
Cascade	I205	Cascade_MS	Cascade_MS
Gorge	Duncan_Creek	Duncan_Creek	Duncan_Creek
Gorge	Hamilton_Channel	Hamilton_Channel	Hamilton_Channel
Gorge	Hamilton_Creek	Hamilton_Creek	Hamilton_Creek
Gorge	Hardy_Creek	Hardy_Creek	Hardy_Creek
Gorge	Horsetail	Gorge_MS	Horsetail
Gorge	Ives	Gorge_MS	Ives
Gorge	Multnomah	Gorge_MS	Multnomah
Gorge	St_Cloud	Gorge_MS	St_Cloud

All that said, here are some results, finally! I fit spawner-to-spawner IPMs with three candidate spawner-recruit functions: exponential, Beverton-Holt, and Ricker. I haven't done formal model comparison using LOO yet, but we can see immediately that the B-H fit is somewhat dubious -- it's basically flat over the range of the data, with very (implausibly?) high intrinsic productivity. In the left panel, the thick curve and shaded 95% credible interval are the ESU-level or hyper-mean S-R relationship, and the thin curves are posterior medians for each of the 12 populations. Similarly, the posterior distribution of intrinsic productivity (alpha) and maximum recruitment (Rmax, in units of spawners) are shown for the ESU and individual populations.

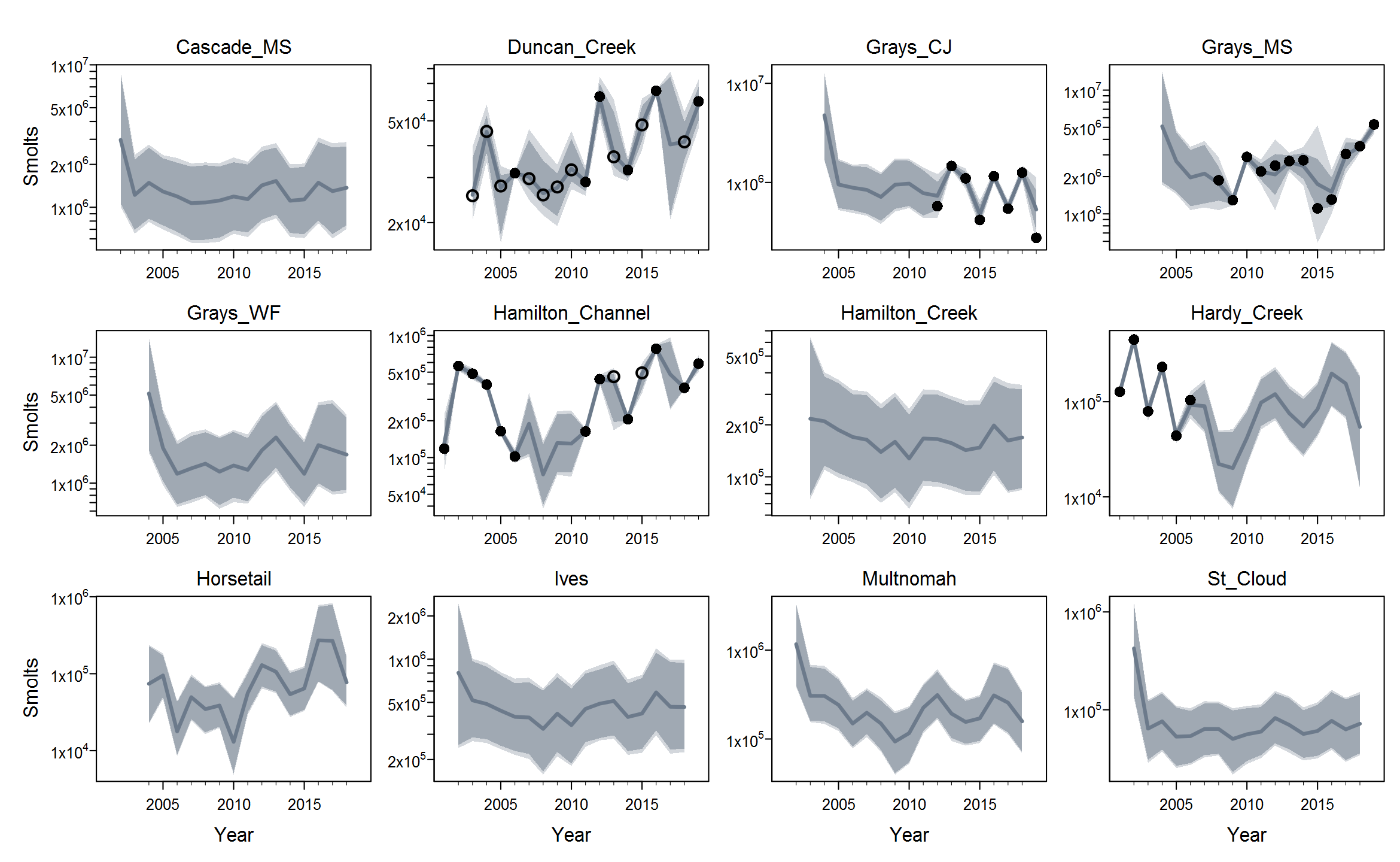
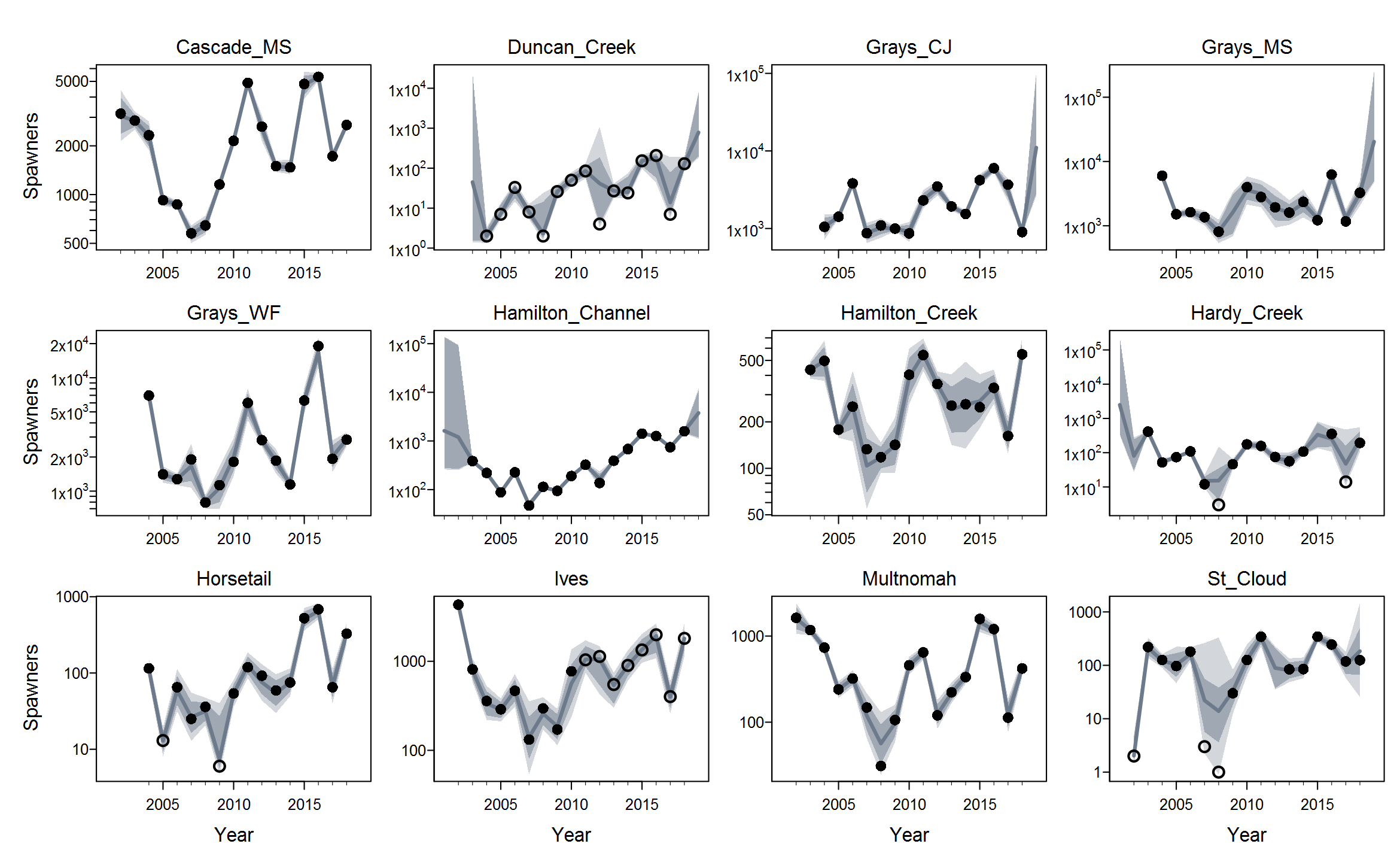
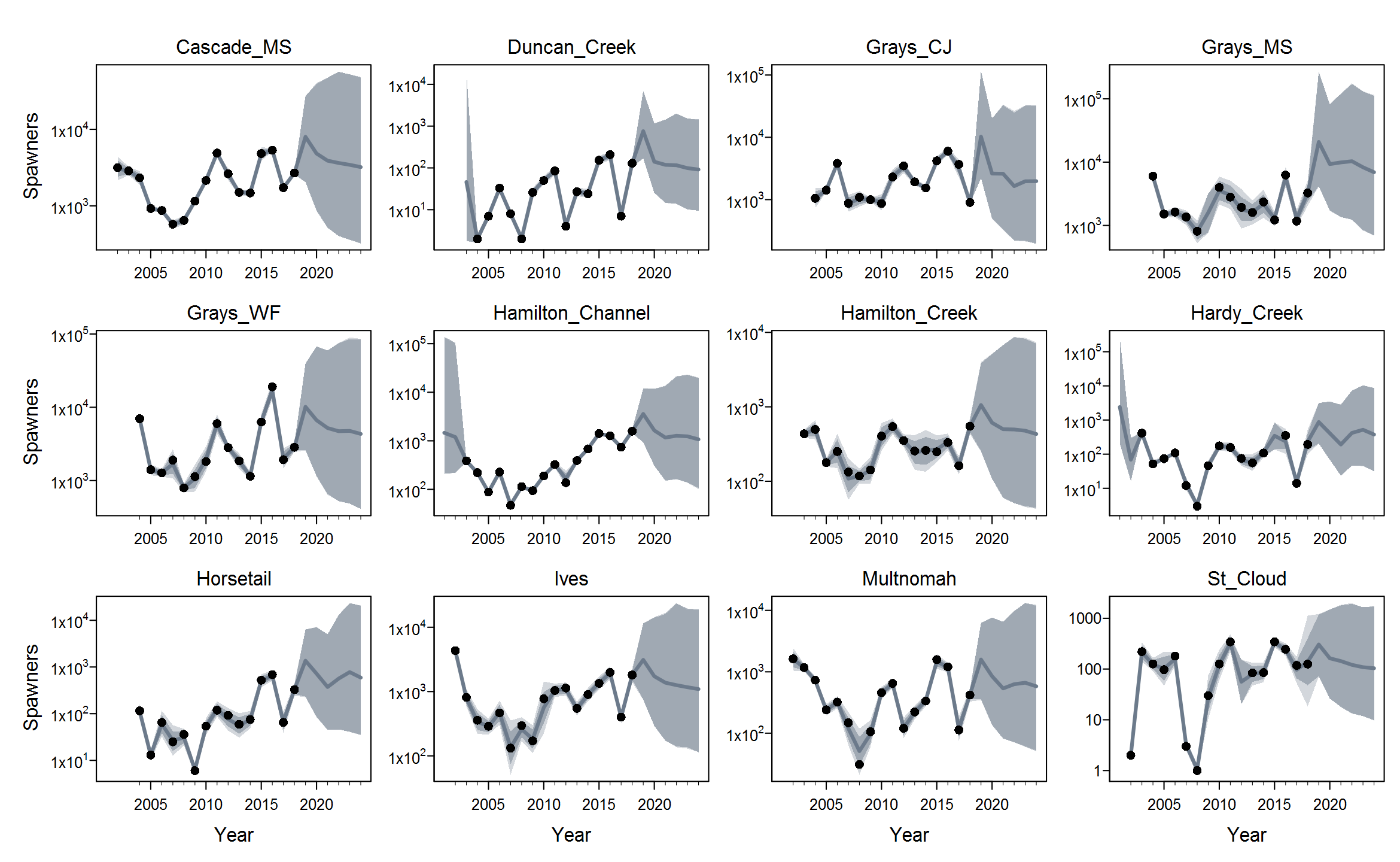
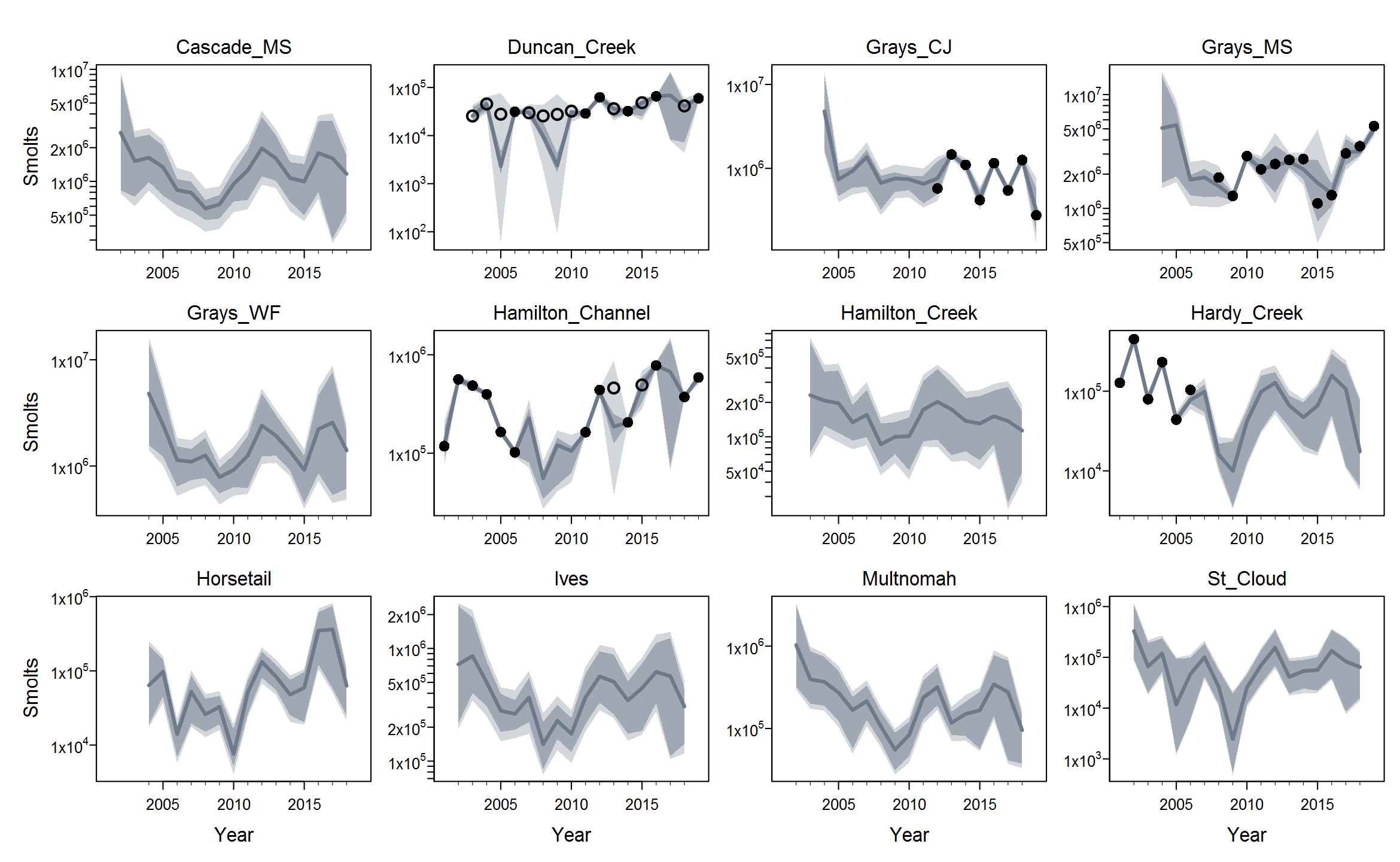
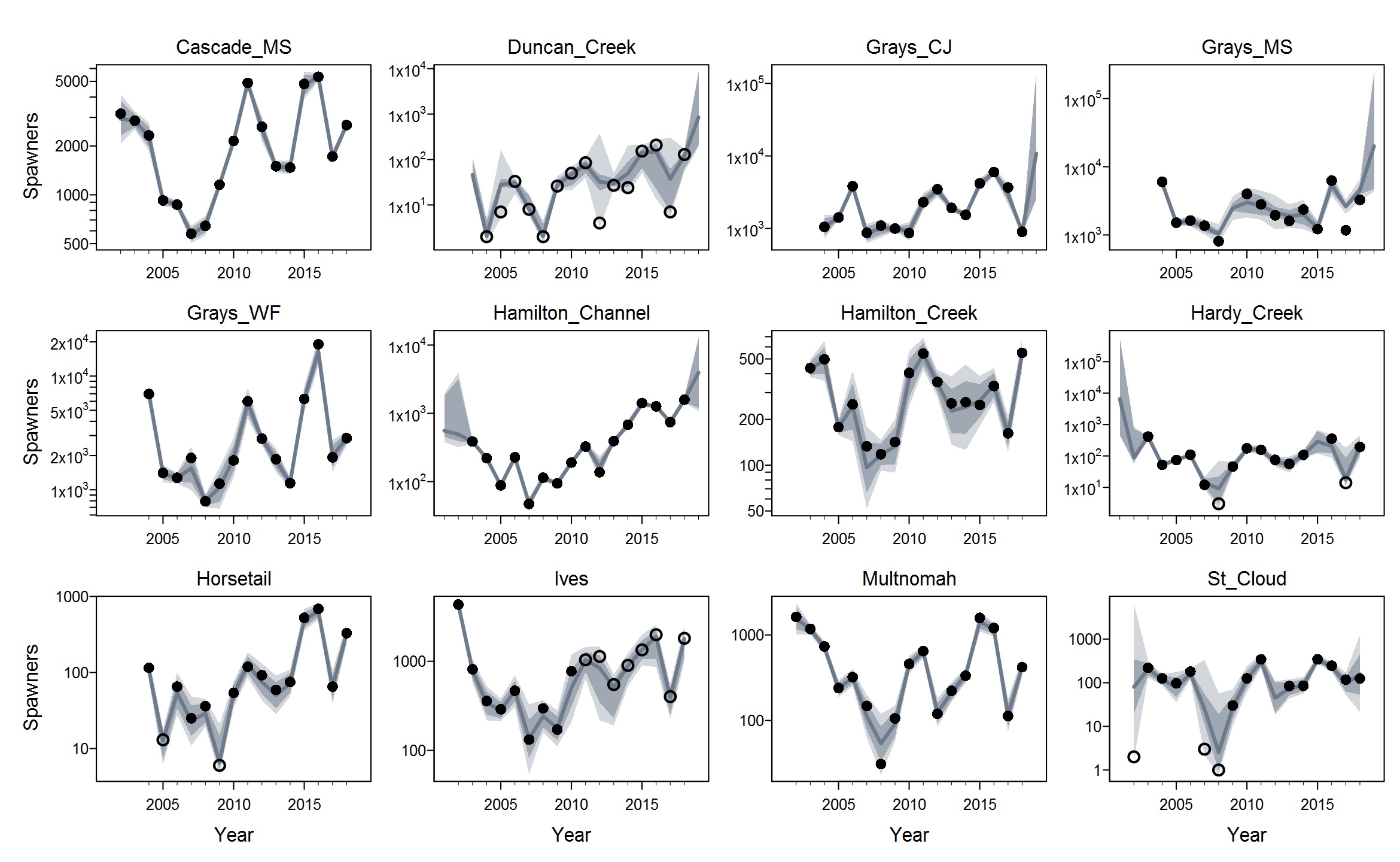
The Ricker estimates look more reasonable, although the S-R curve doesn't approach overcompensation in the estimated range of spawner abundance. As expected, the Ricker produces much lower estimates of intrinsic productivity than the B-H, including a 17% probability that the growth rate is actually negative at the ESU level. Some populations have bimodal posterior distributions of Rmax under the Ricker model. I'm not quite sure what's up with that, but I suspect that using population-specific estimates of spawning habitat (river km or ha) would improve things by making the Rmax random effects more exchangeable when expressed in units of density.

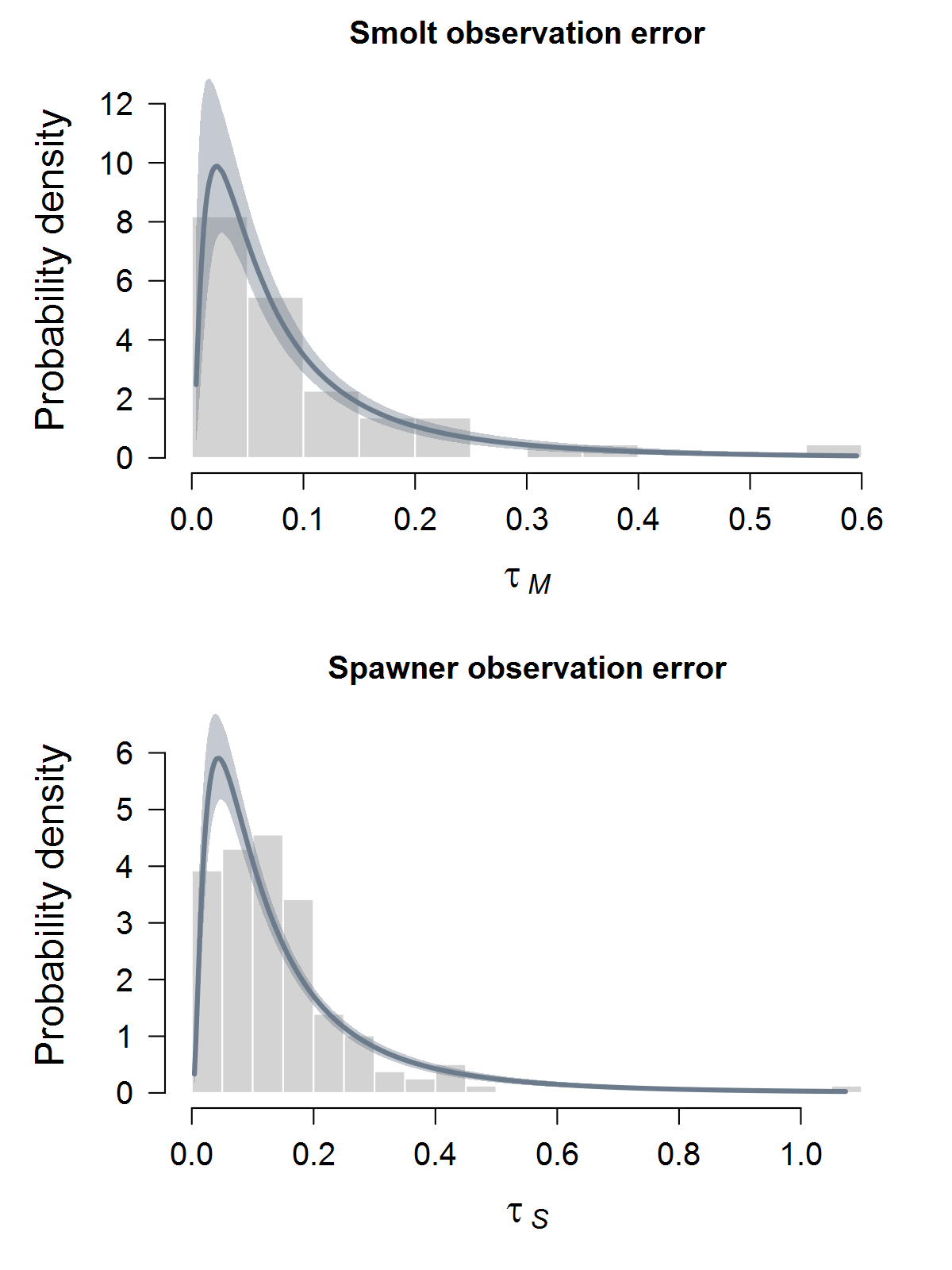
The plots below show the fits from the Ricker model. Points are observed data, lines are posterior medians, and shading indicates the 95% credible interval of the states (dark) or the observations (light). Generally these look pretty good! Interestingly, the four populations in the Gorge_MS group are much less synchronous than you might expect if they were really all highly connected or even quasi-panmictic. That could be one reason why the models struggled to fit the 8-population grouping.

There is of course more due diligence needed for these fits, including more careful prior-posterior comparisons and formal model selection. Next I'd like to integrate the juvenile data and fit two-stage models. And then we can start customizing, perhaps starting with the sample-based observation error estimates.

Any questions / comments / suggestions so far?

Hi Eric,

Thanks for the email. I’ve provided a few quick responses below. Also, I forwarded your email to Thomas and he provided a brief response that I’ve pasted in below, as well.

NAs – I think your “judgment calls” regarding NAs are right. Looking at the raw data, your logic makes sense.
Missing earlier estimates - I noticed this morning that there are (likely) missing estimates of abundance. First, there should be some estimates for 2001 and there are currently none. Second, as you pointed out, there are some instances where NAs are listed for total abundance but biodata exists. I quickly chatted with Todd Hillson this morning and, in short, he said there are some “issues” with estimates from earlier years. We may be able to track down some of these estimates and update the Spawner Abundance .csv file. Curious – as we work on updating the file, would it be helpful (or ok) if we tried to “fix” the zero vs. NAs?
Populations – you updated “Population2” seems fine to me and matches the scale at which the estimates are generated.
Densities – I need to get you population-specific estimates of spawning habitat. Curious, is there a specific unit (length, area) you would want these in? Also, does the model allow these units to change by year? I can work on getting these estimates to you ASAP – do you have a specific date when you would want them?

If it would be helpful, we could plan on having a check-in phone call sometime soon to discuss any remaining issues, results, and next steps.

Kale

*** Here’s Thomas’ email:

A couple quick comments without fully diving in:

Surprised estimated spawners diverge so much from observed spawners…with our observation error estimates being generally very low (CV ~ 5% often), would have thought they would have matched closer…do these results actually make use of the observation error estimates? If so, as priors or fixed?
Productivity parameter modeled hierarchically makes sense either for 1 stage model… for 2 stage model could explore a mixed model:

log(alpha_freshwater) = mu + XB + eps

where: mu is the grand mean XB is a design matrix of habitat “types” (mainstem, constructed spawning channel, off channel). Betas could be modeled as random effect. eps ~ N(0, sigma) is a population specific residual from the mixed model

and

log(alpha_ocean) = mu + XB + eps mu is the grand mean X is a column with the distance from the ocean by population and B is a coefficient describing the effect of distance from river mouth on average marine survival eps ~ N(0, sigma) is a population specific residual from the mixed model

capacity parameter I believe can be modeled as a mixed model:

log(capacity) = mu + log(km^2 of habitat) + eps

where: mu is the grand mean log(km^2 of habitat) is an offset term (you need to supply a coarse estimate of available (as opposed to used) spawning habitat…I can review these with you eps ~ N(0, sigma) is a population specific residual from the mixed model

The rationale for the models above is that productivity in the two stage model can be divided into freshwater and ocean…the freshwater part could be explained by habitat type, which affects max egg to fry survival (productivity) and spawning habitat quantity (capacity), where as the saltwater component could be affected by distance from the ocean (if fry take a beating in the Columbia, the further up they are).

Misc questions:

how are you dealing with harvest removals? (todd may have estimates over time…yes minimal but may wish to include, particularly if they differentially affect pops)
how are you dealing with broodstock removals or importation of spawners/eggs/fry from other pops (Duncan Channels, Grays hatchery)?
Recruitment process errors…are these being modeled as an AR1 model? Univariate or multivariate? If multivariate, spatial or non-spatial prior? Would recommend multivariate…maybe start with non-spatial prior (LKJ for correlation matrix?)…when 2 stage model, maybe good to discuss modeling process error residuals among populations....gets trickier/more options… Are we eventually going to include hatchery pops? How ?

Hi @kalebentley, first things first: that email is just an auto-generated GitHub notification redirecting you to this issue thread so we can discuss here (i.e., don't reply to the email). It looks like Thomas is not yet a collaborator on this repo -- @mdscheuerell, could you invite him?

NAs – I think your “judgment calls” regarding NAs are right. Looking at the raw data, your logic makes sense.

Cool, thanks.

Missing earlier estimates - I noticed this morning that there are (likely) missing estimates of abundance. First, there should be some estimates for 2001 and there are currently none. Second, as you pointed out, there are some instances where NAs are listed for total abundance but biodata exists. I quickly chatted with Todd Hillson this morning and, in short, he said there are some “issues” with estimates from earlier years. We may be able to track down some of these estimates and update the Spawner Abundance .csv file. Curious – as we work on updating the file, would it be helpful (or ok) if we tried to “fix” the zero vs. NAs?

Yes, both of those things would be very helpful.

Densities – I need to get you population-specific estimates of spawning habitat. Curious, is there a specific unit (length, area) you would want these in? Also, does the model allow these units to change by year? I can work on getting these estimates to you ASAP – do you have a specific date when you would want them? If it would be helpful, we could plan on having a check-in phone call sometime soon to discuss any remaining issues, results, and next steps.

The units of A are arbitrary as far as the model is concerned, so I'd go with whatever is available and makes the most sense (e.g., if stream width varies greatly, maybe area is more useful than length). A can be time-varying, but all values need to be in the same units. I'll incorporate these estimates as soon as they're available, but it's not the most urgent need; until then, I can keep using A == 1 (i.e., Rmax in units of spawners).

I'd be happy to chat by phone anytime this week. Probably the next thing I'll need help with is making sense of the juvenile data.

*** Here’s Thomas’ email: A couple quick comments without fully diving in:

Surprised estimated spawners diverge so much from observed spawners…with our observation error estimates being generally very low (CV ~ 5% often), would have thought they would have matched closer…do these results actually make use of the observation error estimates? If so, as priors or fixed?

So this is just the vanilla, off-the-shelf, adult-to-adult salmonIPM model exactly as described in our Tech Memo. It doesn't use any sort of prior information on tau, the spawner observation error SD. Using the sample-based SD estimates is definitely on our list of customizations, and it's probably the first item I'll tackle after we get the off-the-shelf 2-stage model working. As we've discussed before, though, this raises some difficulties. This topic deserves its own issue, but briefly:

(1) The sample obs errors are expressed as SDs, presumably (?) based on an asymptotic normal approximation at the MLE, but the model needs log-SDs for a lognormal observation likelihood. One could come up with some moment-matching kludge, but it's not ideal. When we talked in the Boat St parking lot, you were thinking of redoing these estimates in a Bayesian setting so we could work with posterior summaries directly. Any progress on this?

(2) Should sample-based obs error estimates be regarded as priors on the S states or as known SDs for the S_obs likelihood? This is the issue that you, @mdscheuerell and I discussed at length on the SAFS whiteboard last year. In principle, I think they are priors on the states. The problem is that putting a prior on a nonlinearly transformed parameter requires a Jacobian adjustment, and the Jacobian for S as a function of the primitive parameters is...hopeless. For that reason, I've resigned myself to treating (some transformation of) the sample SDs as arguments to the likelihood. They would themselves have their own likelihood, which would allow imputing the missing SDs.

You're right, though, I did notice in these initial fits that tau is larger than the sample-based SD estimates seem to suggest, given the above caveats. Here's a comparison of the unique (pop x year) recruitment process error, the total recruitment process error (including also the shared synchronous component, which dominates the total so much that it's visually indistinguishable), and the spawner observation error:

Productivity parameter modeled hierarchically makes sense either for 1 stage model… for 2 stage model could explore a mixed model: log(alpha_freshwater) = mu + XB + eps where: mu is the grand mean XB is a design matrix of habitat “types” (mainstem, constructed spawning channel, off channel). Betas could be modeled as random effect. eps ~ N(0, sigma) is a population specific residual from the mixed model

and

log(alpha_ocean) = mu + XB + eps mu is the grand mean X is a column with the distance from the ocean by population and B is a coefficient describing the effect of distance from river mouth on average marine survival eps ~ N(0, sigma) is a population specific residual from the mixed model

Yes, for sure. To be clear, salmonIPM already includes the ability to specify covariates in the hierarchical recruitment process model, but the options for where those covariates enter the model are limited. Allowing more flexible specification of covariates affecting specific parameters has been on the to-do list for a while.

capacity parameter I believe can be modeled as a mixed model:

log(capacity) = mu + log(km^2 of habitat) + eps where: mu is the grand mean log(km^2 of habitat) is an offset term (you need to supply a coarse estimate of available (as opposed to used) spawning habitat…I can review these with you eps ~ N(0, sigma) is a population specific residual from the mixed model

The way salmonIPM handles the spawning habitat "offset" is even simpler -- basically the S-R function is evaluated in units of density, and recruit density is then multiplied by area. This of course ties back into my point about exchangeability and @kalebentley's questions about habitat area above.

Misc questions:

how are you dealing with harvest removals? (todd may have estimates over time…yes minimal but may wish to include, particularly if they differentially affect pops)

Based on discussion with @kalebentley, I assumed harvest was zero. If there are nonzero estimates, yes, let's include them.

how are you dealing with broodstock removals or importation of spawners/eggs/fry from other pops (Duncan Channels, Grays hatchery)?

This was one of the trickiest parts of the raw data to wrap my head around, but with @kalebentley's help I think I've got it sorted for the off-the-shelf models. Broodstock removals from naturally spawning populations are straightfoward, based on disposition. All spawners returning to a given population in a given year with "hatchery" dispositions are summed to get the B_take_obs field in the salmonIPM data format. As for importations, the generic model estimates hatchery-origin spawner inputs (p_HOS, informed by the observed H/W frequencies) independently for each pop and year where they are known or suspected to be present. However, there is no way to model directly observed transfers of spawners from one natural population to another -- any "population" that receives such transfers is treated as a hatchery and its dynamics are not explicitly modeled. Hence, in the designations @kalebentley and I came up with, Duncan Creek is a population but both Duncan Channel and Duncan Hatchery are hatcheries, and fish disposed from the former to the latter are treated as broodstock removals.

Are we eventually going to include hatchery pops? How ?

Yes, we'd hoped to do that. As the above suggests, it's more complicated than I originally envisioned, especially because some locations (e.g., Duncan Channel) have characteristics of both hatcheries (broodstock intentionally transferred there) and natural populations (spawning occurs naturally; fry releases not directly quantified). This will bear more discussion for sure, in a separate issue.

Recruitment process errors…are these being modeled as an AR1 model? Univariate or multivariate? If multivariate, spatial or non-spatial prior? Would recommend multivariate…maybe start with non-spatial prior (LKJ for correlation matrix?)…when 2 stage model, maybe good to discuss modeling process error residuals among populations....gets trickier/more options…

Yes, this is all laid out in the Tech Memo, but basically the shared recruitment process errors are AR(1) and the unique recruitment process errors are IID. That induces a correlation structure, but it's not as flexible as a MAR(1) with unconstrained error covariance matrix. In past experience I've concluded the latter is way more trouble than it's worth; and as you say, it would get even uglier in a multi-stage model. We can look at the process error residuals to see how much spatial structure we might be missing.

Hi @kalebentley (it looks like Thomas still isn't a collaborator?):

Now that I've spent most of this month chasing that obscure Stan bug, we can finally get back to Lower Columbia chum!

I've updated all the IPMs with new and improved priors on the initial states (spawner abundance and age structure), which has been on the salmonIPM issue list for many moons. This was a surprisingly tricky problem and I won't belabor the details here, but the new approach takes advantage of more information from the process model for spawners-at-age predictions in years 1:max_age and relies less on the initial-state priors, which effectively gives the process model more "data" to work with. In long time series the difference is negligible, but in short ones (such as ours) it can actually be noticeable.

Let's look at some results from the two-stage (spawner-smolt-spawner) model. This one hasn't been formally written up yet, but it's a pretty straightforward extension of the spawner-to-spawner model. The smolt recruitment process model in the former is directly analogous to the adult recruitment process in the latter, including both the shared autoregressive and unique IID process error components. SAR is modeled with a common hyper-mean and, again, an autoregressive process error common to all populations plus a unique IID process error (both logistic normal, in this case). The hierarchical model for adult age structure is the same as in the spawner-to-spawner IPM. The only addition to the observation model is a likelihood component for smolt abundance; like spawner abundance, it is assumed to be lognormal with a global log-SD.

All the results shown below are for the Ricker spawner-smolt recruitment function. I have attempted to do model selection using LOO for both the spawner-to-spawner and two-stage IPMs, but the preponderance of "badly behaved" pointwise likelihoods (those with extremely skewed posterior distributions, representing highly influential observations) renders the results uninterpretable. I'll leave this topic for another time, although I can see @mdscheuerell nodding in commiseration. We will probably have to resort to a more creative (read: computationally painful) approach to formal model selection, i.e. brute-force cross-validation. For now, the Ricker seems at least as plausible as the other two S-R functions. Here's what it looks like:

There are still those wonky bimodal posteriors of some Rmax random effects, which potentially might improve if we had population-specific habitat area estimates.

These are the fits to spawner abundance:

You might notice that the time series for some populations are slightly longer than they were for the spawner-spawner model. That's because the smolt time series may begin earlier or extend later than the spawner time series (so the predictions after the last spawner observation are not actually step-ahead forecasts). I'm still truncating the time series by requiring spawner and/or smolt observations; I did try re-fitting the spawner-spawner models while including those early years that have BioData only, but even with the new initial-state priors there was a lot of uncertainty and not much useful information.

Here are the fits to smolt abundance:

It's actually impressive that the IPM is able to extract this much information from what are undeniably sparse data -- five groups (two with few observations) is often considered a rough minimum for hierarchical modeling, and yet all the hyperparameters are identifiable and the sampler is reasonably well-behaved. And of course the beauty of hierarchical state-space is that you get hindcasts of states even when you didn't collect any data!

On a similar note, the shared process error anomalies for smolt recruitment and SAR are enlightening:

The SAR anomalies look quite similar to the shared recruitment process error anomalies in the spawner-spawner model (note the different start years, as explained above, and of course outmigration year is brood year + 1):

So the two-stage model has inferred, quite plausibly, that all the synchrony in adult recruitment is coming from SAR while freshwater productivity is essentially independent. Not bad for partial smolt observations from fewer than half the populations!

It will be interesting to see how the inclusion of pointwise smolt and spawner observation error priors refines this picture -- my guess is that they will tighten the observation error in most cases, which will force the process model to do less aggressive smoothing. And hopefully incorporating the age-specific fecundity data will give us more accurate and precise predictions of smolt productivity, and maybe (dare to dream) help nail down the shape of the S-R function.

As always, comments and questions are welcome.

Good morning @ebuhle,

First off, sorry for the delay in responding to your last post. I read through it immediately but admittedly my brain is a bit slow when it comes to these topics so I knew I would need more time to re-read the post and digest the information when I had more time.

Second, I appreciate the added humor re: Walter White.

Third, this all looks great and clearly you are making really good progress. I don't have any feedback that will directly help with the model development but I do have a couple of questions/comments:

(1) Outside of some graduate-level courses, I don't have a lot of experience "model fitting" with the Ricker S-R function. Therefore, I just want to verify I am understanding the output you provide - i.e., what exactly is alpha and Rmax? I assume one relates to "productivity" (alpha?) and the other to "capacity" (Rmax) but my attempt to quickly refamiliarize myself with this information by scanning through some online documents (here, here, here) wasn't 100% successful. For the novice in the group, would you mind providing a quick tutorial?

(2) Regarding your comment ("There are still those wonky bimodal posteriors of some Rmax random effects, which potentially might improve if we had population-specific habitat area estimates") -- working with one of our GIS guys, I am starting to make a bit of progress on quantifying spawning habitat for the 12 populations we've identified. There are obviously lots of ways to approach quantifying this variable. In an effort to keep this simple, at least at first, I'll take a first cut and then we can always go back and re-estimate.

(3) You wrote "You might notice that the time series for some populations are slightly longer than they were for the spawner-spawner model. That's because the smolt time series may begin earlier or extend later than the spawner time series (so the predictions after the last spawner observation are not actually step-ahead forecasts)." Can you help me understand? It appears as though only the four populations that had juvenile data from 2019 have an estimate (prediction?) from spawners in 2019? If this isn't a one-step ahead estimate, what is it?

(4) In looking at the time-series plots of juvenile abundance by population, the model fit to the observed data doesn't look particularly great. I totally understand what you are saying ("It's actually impressive that the IPM is able to extract this much information from what are undeniably sparse data") but just curious if you could elaborate here. Could fits be improved with habitat data (or like you mentioned, age-specific fecundity data)? For instance, when I look at the Grays-CJ plot, the fit looks more-or-less like a straight line through the data points.

(5) You wrote ("It will be interesting to see how the inclusion of pointwise smolt and spawner observation error priors refines this picture ") - what exactly does this mean? Does this pertain to using the estimated observation error to "weight" the influence of the observations?

(6) Lastly, I haven't forgotten about the desire to update the juvenile abundance spreadsheet (with means opposed to just the medians) as well as reconciling the missing adult estimates (NAs) in early years (2001 - 2004) where biodata exists.

Ok - that's it for now. Thanks again for all your efforts on this. This is really exciting.

Kale

Hi @kalebentley et al.

First off, sorry for the delay in responding to your last post. I read through it immediately but admittedly my brain is a bit slow when it comes to these topics so I knew I would need more time to re-read the post and digest the information when I had more time.

No worries, and you're not alone!

(1) Outside of some graduate-level courses, I don't have a lot of experience "model fitting" with the Ricker S-R function. Therefore, I just want to verify I am understanding the output you provide - i.e., what exactly is alpha and Rmax? I assume one relates to "productivity" (alpha?) and the other to "capacity" (Rmax) but my attempt to quickly refamiliarize myself with this information by scanning through some online documents (here, here, here) wasn't 100% successful. For the novice in the group, would you mind providing a quick tutorial?

Sure. In salmonIPM we parameterize both the Beverton-Holt and Ricker S-R functions such that the parameters have a consistent interpretation: alpha (intrinsic productivity) is the slope at the origin, i.e. recruits per spawner in the absence of density-dependence, and Rmax is maximum recruitment, i.e. the asymptote of the B-H or the peak of the "dome" of the Ricker. I was going to refer you to the Tech Memo for details, but then I remembered we only give the eqn for the B-H there. GitHub issues don't support LaTeX, so for now this Stan code chunk will have to do (note that A is spawning habitat area and all the functions are in terms of spawner density, S/A):

  // spawner-recruit functions
  real SR(int SR_fun, real alpha, real Rmax, real S, real A) {
    real R;

    if(SR_fun == 1)      // discrete exponential
    R = alpha*S/A;
    else if(SR_fun == 2) // Beverton-Holt
    R = alpha*S/(A + alpha*S/Rmax);
    else if(SR_fun == 3) // Ricker
    R = alpha*(S/A)*exp(-alpha*S/(A*e()*Rmax));

    return(R);
  }

This parameterization of the Ricker is nonstandard, but in addition to being interpretable I've found it to be better-identified than the textbook versions, as is typically the case when model parameters correspond to well-defined features of the data. And of course it's simple to solve for any parameterization in terms of any other.

Just to make sure we're on the same page, the key difference between the IPM approach and what you likely learned in grad school about fitting S-R models is not the parameterization, but the fact that the S-R function in the IPM is embedded in the process model. The state-space framework is fundamentally different from the traditional regression approach where you'd do a run reconstruction to "calculate" R and then regress it (or some linearizing transform thereof) against S. In state-space / IPM-land, R is a hidden state variable, not "data". The data are what you actually observe, e.g. spawners and age-frequencies, and the run reconstruction, as it were, happens jointly with all of the other parameter estimation.

As an aside, the terms "productivity" and "capacity" seem to engender confusion among fisheries scientists. Productivity (e.g., R/S) is a function of parameters and the current state S, but people often use the term (and sometimes the actual quantity!) when they mean the parameter alpha. And in population ecology, "carrying capacity" refers to the nontrivial equilibrium point at which the production function crosses the 1:1 replacement line (i.e., R = S, ignoring any harvest or other mortality), but fisheries people often use "capacity" to mean various other things, such as the B-H asymptote that I call Rmax. Confused yet?

On a more substantive note, I'm a little skeptical about claims that threatened species are subject to overcompensation, but then I don't know much about the natural history of LCR chum. Do you find it plausible that they reach high enough densities to experience "scramble" competition for prime spawning habitat, redd superimposition, etc.? Like I said upthread, the B-H fits are even more of a stretch -- basically a ski jump at the origin and a plateau over most of the range of the data -- and that remains true in the two-stage model. At least the Ricker gives a more believable estimate of intrinsic productivity, which translates to more precautionary inferences about quasi-extinction risk and so on.

(2) Regarding your comment ("There are still those wonky bimodal posteriors of some Rmax random effects, which potentially might improve if we had population-specific habitat area estimates") -- working with one of our GIS guys, I am starting to make a bit of progress on quantifying spawning habitat for the 12 populations we've identified. There are obviously lots of ways to approach quantifying this variable. In an effort to keep this simple, at least at first, I'll take a first cut and then we can always go back and re-estimate.

Awesome, thanks. And I agree, this can be an iterative task.

(3) You wrote "You might notice that the time series for some populations are slightly longer than they were for the spawner-spawner model. That's because the smolt time series may begin earlier or extend later than the spawner time series (so the predictions after the last spawner observation are not actually step-ahead forecasts)." Can you help me understand? It appears as though only the four populations that had juvenile data from 2019 have an estimate (prediction?) from spawners in 2019? If this isn't a one-step ahead estimate, what is it?

You're exactly right: only the populations with data (smolts, in this case) in 2019 have estimated states (both smolts and spawners) shown in 2019. I didn't want to throw out precious smolt observations, so I included those terminal years that have smolt but not spawner data. By contrast, a one-step-ahead forecast would be a projection beyond the end of any data. In fact, the simplest way to generate forecasts in salmonIPM is just to pad fish_data with extra final years containing no data, but that's not what I've done here.

(4) In looking at the time-series plots of juvenile abundance by population, the model fit to the observed data doesn't look particularly great. I totally understand what you are saying ("It's actually impressive that the IPM is able to extract this much information from what are undeniably sparse data") but just curious if you could elaborate here. Could fits be improved with habitat data (or like you mentioned, age-specific fecundity data)? For instance, when I look at the Grays-CJ plot, the fit looks more-or-less like a straight line through the data points.

In general, what's going on is that the model is trying to accommodate various likelihood components: spawner and smolt observations, as well as spawner age- and origin-frequencies. The joint posterior represents a compromise among all of these, plus the priors (to include the top-level priors on the hyperparameters as well as the various hierarchical and state-space process model components). The more information-rich data types naturally tend to weight more heavily in the posterior, which is why the model tracks the spawner observations more closely than it does smolts. There isn't nearly as much information to constrain the spawner-smolt stage as there is to identify the overall life-cycle productivity.

This kind of situation comes up routinely in integrated stock assessment models, and there's a huge literature (which I don't pretend to know in detail) on related considerations in that context. It's not necessarily a problem per se; the model is just interpreting how much information the data provide about various processes, taken all together. In that sense, it's useful to see which data types fit better than others. That said, yes, I'm cautiously hopeful that some of the model developments we're working on may explain more of the variation in smolts. Standardizing by spawning habitat might help, but I suspect age-specific fecundity will matter more since it provides a time-varying adjustment to freshwater productivity. And the sample-based observation errors might be just as informative; see below.

(5) You wrote ("It will be interesting to see how the inclusion of pointwise smolt and spawner observation error priors refines this picture ") - what exactly does this mean? Does this pertain to using the estimated observation error to "weight" the influence of the observations?

Yes, exactly. So far we've been looking at the "basic" salmonIPM models, which don't assume any external knowledge of the magnitude of observation error; there's just a global lognormal obs error SD for spawners and another one for smolts, given "noninformative" priors. As Thomas pointed out, the model-based estimates of those SDs seem larger than your sample-based estimates in most cases (with the caveat that it's not straightforward to convert the latter into the same currency as the former, as we've discussed). Using the sample-based estimates as priors will, I expect, weight the spawner and smolt observations more heavily (though not all equally so) in the joint posterior, forcing the process model to admit more underlying stochasticity (i.e., do less aggressive smoothing) as it tries to track the data more closely.

(6) Lastly, I haven't forgotten about the desire to update the juvenile abundance spreadsheet (with means opposed to just the medians) as well as reconciling the missing adult estimates (NAs) in early years (2001 - 2004) where biodata exists.

Sweet, thanks for reminding me. It's super easy to re-run all of these models as data get updated or revised.

Hi @kalebentley, we've got some interesting new results. The custom-built LCR chum IPM now incorporates the "known" observation error SD corresponding to each smolt and spawner abundance estimate.

To compute these from the data, I assumed that the columns originally named Abund_Mean and Abund_SD (for smolts) or Abund.Mean and Abund.SD (for spawners) are the mean and standard deviation, respectively, of the Bayesian posterior distribution of abundance based on the sample data and the specified analysis method, and that this posterior distribution is approximately lognormal. This was my understanding from our phone conversations, but please correct me if I missed something -- in particular, if some or all of these estimates are in fact MLEs and asymptotic standard errors based on the Hessian, then my calculations will be wrong. Given those assumptions, though, it's straightforward to solve for the log-SD parameter of the posterior distribution, which is then plugged in as the SD of the lognormal observation error likelihood (tau_M or tau_S for smolts or spawners, respectively) in the IPM.

One additional complication is what to do with those smolt abundance estimates where Abund_SD==0, which occurs when Analysis=="Census" (some years in Duncan Creek and Hamilton Channel). I realize these are streams with weirs, but since other years in the same populations use different analysis methods (e.g., "P-Spline") and report nonzero observation error SDs, I assumed that the "Census" counts are not actually perfect but simply have unknown precision, so I replaced the zeros with NA.

All of the missing observation error SDs are imputed within the IPM in the manner that we discussed on the phone with Thomas. That is, the "known" SDs for each life stage are modeled with a lognormal distribution whose parameters (e.g., mu_tau_S and sigma_tau_S in the case of spawners) are estimated, and the missing values are filled in with the median of this distribution. In reality, the distribution of observation error SDs probably differs across populations and sampling / analysis methods, but given the sparsity of the data I didn't try to model this variation; I just assumed all the SDs within each life stage are drawn from a common lognormal hyperdistribution. This is what those fitted hyperdistributions look like:

OK! All that said, this does change the results quite a bit, unsurprisingly. The general story is that, as we anticipated, the sample-based SDs are much smaller than the naive IPM-based estimates. Because of this increased precision in the observation model, more of the variation gets squeezed into the process errors -- the process model is forced to be more dynamic in order to more closely track the data. Or to put it another way, the model performs less smoothing of the data. Again, this is exactly what you'd expect, but it was startling to actually see this level of precision. I almost felt like I must've done something wrong, LOL.

That precision propagates into more precise estimates of the process model parameters, including the spawner-recruit functions. The model has less wiggle room about what the hidden states actually are, since they have to be pretty close to the data. (Of course, there's more uncertainty when the observation and/or the observation error SD is missing.) One interesting side effect is that now LOO appears to favor the Beverton-Holt over the Ricker, and both of them over the density-independent model. Unfortunately, the LOO estimates are still just as badly behaved as before, so we should take this with a huge salt lick. But the fitted B-H function looks more biologically reasonable than before, with a productivity parameter that's within the realm of possibility.

Ricker:

Beverton-Holt:

Some of the population-specific Rmax posteriors still have that weird lumpy thing going on, but keep in mind that we still aren't using habitat area as an offset.

Here are the Beverton-Holt fits for smolts:

And spawners:

Like I said, the precision is kind of shocking. A less pleasant side effect is that, because the process noise is forced to increase, the forecast uncertainty blows up much more quickly:

These results are all incorporated in the vignette. I'm afraid the text is still skeletal; I've been doing more coding than writing. If it's OK with you, I might keep going -- the next item is modeling the fecundity data, and if all goes well that should be doable in the next couple of days.

From the email zone, Thomas writes:

Yes, Eric, adding in known precision for observations makes a HUGE difference! One tweak I’d suggest here is actually fixing the census precision instead of estimating…years with Census should have lower error than years with spline estimates. I’d use a lognormal sd of 2-5%...honestly, results will not be sensitive to which you choose. But should tighten the model more and is consistent with how Fleischman modeled observation error for weir data.

True, we could use an informative prior on tau_M when Analysis=="Census", although I'd prefer one with some uncertainty rather than a point mass. But there's always that trade-off between detail and simplicity (of code and of explanation) when you start carving out special cases for smallish subsets of data. FWIW, I realized I was doing the imputation wrong; the unknown observation error SDs should be drawn from the lognormal hyperdistribution, not set equal to its median. Doing it correctly ends up allowing a bit more uncertainty, of course, but doesn't fundamentally change the story. Anyway, the posterior median of the imputed values isn't too much bigger than what you're suggesting -- around 0.06, with 90% CI roughly (0.01, 0.35). At some point it might be worth revisiting the idea of allowing tau_M to depend on TrapType as a covariate (since all three trap types have some non-missing SD estimates), but we'd have to decide what to do about the ~50 cases where both TrapType and Analysis are NA. Like you said, though, I doubt any of this would make a huge difference.

Presumably similar considerations apply to the spawner observation error, but in that case the only two methods that have non-missing CVs ("Carc tagging" and "Live tagging") are basically indistinguishable.

I’ve seen same phenomenon with BH vs Ricker…and you can demonstrate with simulation….simulate BH data, then add obs error and eventually model will select Ricker over BH.

Interesting. I would've expected the reverse, at least in the regression framework, b/c the observation error smears out the "predictor" (spawners) and makes the relationship appear flat. In the state-space context, I haven't seen any consistent model selection biases when fitting simulated data with salmonIPM, but I have seen a Bayesian analogue of the "unbounded likelihood profile for alpha" pathology that Barrowman and Myers (2000) described. I've only seen this when fitting data from a single population, though; the multi-stock hierarchical model seems to be much more robust.

Anyway, I guess this is a little different in that we're fitting data that have some "true" level of observation noise, using the state-space framework, and the issue is whether we have informative priors with a small observation CV or just let the model figure it out.

TBH, the actual spawner-smolt relationships (either observations or states) are pretty funky. Some classic shotguns, others with crazy outliers or L-shapes, and a few reasonable-looking ones. I have a plot that illustrates this, but I'm waiting for some models to finish running before I can upload it. I'm sure this is why the "naive" IPM concludes that the observation error must be fairly large, and smooths the data aggressively. There's only so much the process model can do to make sense of the dynamics.

On the same note, I should stress again that the model selection results from LOO are not at all trustworthy because of the severely skewed posterior distributions of pointwise likelihood (most of the Pareto k estimates are in the "bad" or "very bad" category). I lean toward the B-H over the Ricker here on scientific, not statistical grounds -- it just seems unlikely that these populations would be experiencing overcompensation. At some point when the model structure is more settled, we'll probably have to bite the bullet and do brute-force cross-validation to rank the S-R functional forms.

I agree next place to go is fecundity…likely can use this stage to constrain upper bound of productivity parameter for BH, which is always a challenge

:+1:

Habitat offsets will definitely help the Rmax

:+1:

Also, I have a question / request for you or @kalebentley: the juvenile data includes both the mean and median of the posterior distribution of abundance from the observation model (again, set me straight if I'm misunderstanding the Bayesian-ness of these estimates) but the spawner data only includes the mean. Upon reflection, I realized that the median of the (presumed) lognormal is actually what we want to treat as the "point estimate" in order for this likelihood-as-prior trick to work. Granted, the two are pretty similar when the CV is small, but I'd prefer to work with the median if it's available. Of course I could calculate the median from the mean and SD, but there are many cases where Abund.Mean is reported but Abund.SD is NA.

OK, here are some results from a first pass at the spawner-egg-smolt-spawner IPM.

The density-dependence occurs during egg deposition according to a S-R function parameterized by intrinsic productivity and egg "capacity" Emax, where the parameter formerly known as alpha is now a function of female fecundity. Specifically, intrinsic productivity is the weighted average of age-specific fecundity, weighted by the estimated spawner age structure, divided by 2. This assumes (1) wild female age composition is the same as overall wild spawner age composition, which appears valid (strikingly so, in fact) for these data, and (2) the sex ratio is 50:50, which is definitely not true in general (more on this later). By expanding the IPM in this way, we introduce an additional source of variation into the process model by allowing intrinsic productivity to vary across populations and through time. That variation isn't a new, independent process error, though. It's forced by variation in spawner age structure, which couples it to the rest of the process model and to the age-comp data, and is further constrained by fitting to the fecundity data.

Density-dependent egg deposition is followed by density-independent egg-to-smolt survival and SAR. Both survival rates are modeled on the logit scale with an AR(1) year-specific anomaly common to all populations and a pop x year unique residual error. Egg-to-smolt survival has an additional population-specific error term, similar to the way cohort age-at-return probabilities are modeled throughout salmonIPM. As before, SAR only has the autocorrelated shared trend and idiosyncratic errors. We could talk about whether these formulations make the most sense or not.

The first set of plots gives an overview of the key parameter or state estimates by life-cycle transition for the Beverton-Holt model. As usual, the thick gray lines correspond to ESU-level hyperparameters with envelope showing the 90% credible interval, and the thin lines are population-specific. Now the S-R curve has to be "reconstructed" by averaging the time-varying intrinsic productivity within or across populations. The biggest thing that jumps out at me here is that egg-to-smolt survival is unrealistically high. I'm not sure what to make of this, but so far it has proven robust to different S-R forms and other slight model tweaks.

Here's the fit to the age-specific fecundity observations. I ended up using a zero-truncated normal likelihood, whose posterior median and 90% CI are superimposed on the histogram of the data.

Like I alluded to in the first paragraph, this "extra" state variable of egg deposition, sans direct observations, doesn't come for free; its process errors are driven by spawner age structure and scaled by estimated fecundity. Another way to say this is that the likelihood now has to balance fitting the fecundity data along with smolt and spawner abundance, age- and origin-frequency. And we are essentially hypothesizing that variations in spawner age composition can explain some of the variation in juvenile and adult abundance. There's no guarantee it will actually fit those data better...see where I'm going with this...

And similarly for spawners:

None of these fits are, like, terrible (well, except for maybe Duncan Creek smolts). But it's interesting to see how forcing the S-R curve with age-weighted fecundity misses certain observations that had previously been accommodated by large recruitment process error residuals. Of course, we do get additional information from this model, e.g. estimates of fecundity, annual total egg deposition (which I didn't show), and egg-to-smolt survival. This model may also attribute less of the overall variation to unexplained process noise, which would tighten up the forecasts; that remains to be seen.

I've been running into some computational difficulty in fitting these models. That was true for the simpler model structures too, but getting worse as we add complexity. Specifically, I'm getting a lot of divergent transitions, even with a pretty conservative step size and hence excruciatingly long runtime. I haven't been able to identify any pattern to the divergences -- they don't appear to concentrate in any region of parameter space -- which suggests they might be "false positives", but warrant caution nonetheless. I have a feeling this may be a case of Gelman's folk theorem in the sense that these data are just pretty noisy and hard to fit well (especially given the very low observation CV we're assuming in many cases), and that lack of fit manifests as the sampler struggling. I'll keep investigating.

I'll conclude for now with some thoughts on what's not in this model, and what to prioritize next:

Age-specific fecundity is global, not population- or year-specific. We might consider allowing hierarchical variation at the MPG / strata level by mapping the hatchery locations where fecundity was measured to the wild population strata, but it doesn't look like there is much if any difference in fecundity across strata. As for temporal variation, I don't think years are evenly represented enough in the fecundity data to make this worthwhile.
I'm treating the fecundity observations as known without error; the variation shown above is across females. It might be worth incorporating the observation error indicated by 95% CIs in the fecundity spreadsheet, but I would need to know more about what that CI and point estimate represent and how they were derived.
Some quick exploratory plots reveal that the spawner sex-composition samples frequently depart from 50:50, both across populations and through time. These departures are often highly "significant" based on binomial CIs, and in many cases they are pretty extreme. The implications for using age-weighted fecundity to force the S-R function are obvious. IMO this is low-hanging fruit that could make a big difference, for better or worse. I'd put this near the top of the list for our next funding cycle.

Thoughts?

All,

I've only started looking at the LCR chum IPM RMarkdown document a couple of weeks ago and these issue threads just this week. I still don't have my head wrapped around everything, I never likely will when it comes to the R code and modeling terms.
There were some things that jumped out at me when I looked at some of the results graphs in the RMarkdown document. I see some of these talked about in this thread (e.g. unrealistically high egg-to-fry survival rates) and other questions posed in the issue thread that I think I can help.

I’ll start with the easy ones. You mention that sex ratio is way off 50:50 in some instances. I’m guessing these sites are primarily Duncan and Hamilton Spring Channel and I likely know the reason. In the April 4 message you say “Interestingly, the four populations in the Gorge_MS group are much less synchronous than you might expect if they were really all highly connected or even quasi-panmictic. That could be one reason why the models struggled to fit the 8-population grouping.” I’m assuming those four are Ives, Horsetail, Multnomah, and St Cloud. We see a fair amount of movement of fish between Horsetail, Multnomah, and St Cloud as a group and less between that group and Ives. Also, flow (Bonneville tailwater elevation) in some years can play a big part in spawner distribution. While Ives has a decent amount of spawning areas available at low tailwater, the other three are really limited at low tailwater (typical at the start of the spawning season) and prolonged periods of low tailwater and rainfall (important to get usage at St Cloud) can definitely shift fish around. Prolonged periods of low tailwater combined with low rainfall also impact spawner distribution between mainstem sites and tribs (2019 will be a great example).

I think the unrealistically high egg-to-fry survival rates are a combination of two things. One big assumption I’m making is that the survival rates measured at Duncan have a big influence. I’ll talk about issues at Duncan below, re: not including all the adults that could produce fry at the channels.

From the April 6 exchange “Are we eventually going to include hatchery pops? How ? Yes, we'd hoped to do that. As the above suggests, it's more complicated than I originally envisioned, especially because some locations (e.g., Duncan Channel) have characteristics of both hatcheries (broodstock intentionally transferred there) and natural populations (spawning occurs naturally; fry releases not directly quantified). This will bear more discussion for sure, in a separate issue.” I’m a bit confused by this statement, maybe it’s just terminology, Duncan Channel is a complicated site. We have both translocated adults from mainstem spawning sites and adults trapped at the mouth of Duncan Creek and transported into the spawning channel. What has me confused is it seems your treating these two groups separately, which shouldn’t be the case. Regardless of source (mainstem or trap), all adults are released above monitoring weirs in the spawning channels and they are mixed together in some year & channel combinations. That’s why the statement “(spawning occurs naturally; fry releases not directly quantified)” causes me to pause, fry production from the channels is a mix of both adult sources. It’s actually more complicated than that but I can’t remember if your using combined channel fry production or channel specific fry production (did the channel receive only translocated adults (green females only) or a mix of Duncan trap and translocated adults (would likely include partial spawned females)). Which value your using would dictate what mix of adults (mainstem and trap combined or mainstem only) produced the fry.

The second reason I believe is related to what data your using to model fecundity by age. I believe we provided all the estimates of eggs-per-female from our hatchery work. I’m using the term of eggs-per-female because that’s what the data set is, it’s not fecundity. Unlike most hatchery programs, in almost all years we do not use adults that return to hatcheries. In some years they did use adults that recruited to the Grays River or Beaver Creek hatchery swim-in pond, but those are a small component and only in the early years of the program. The majority of brood are collected off the spawning grounds (seining or sight fishing). That means partially spawned females are included in the broodstock in most years. I can see in the code that “reproductive effort” is a column header in the data file but it doesn’t look like you stratify/exclude based on the value. Reproductive effort is the green egg mass weight (g) / female whole body weight (g). We use a reproductive effort value of 16% or greater as a cut off to identify females that likely had spawned in the wild before being collected as brood (based off work Steve Schroder did with Puget Sound chum salmon). When we generated potential egg deposition values at the Duncan Channels to estimate egg-to-fry survival we only use data from hatchery spawned females with > or = to 16% reproductive effort values (assumption is that egg-per-female at spawning = fecundity when reproductive effort meets threshold value). I was pretty sure all eggs-per-female data was being used when I saw the histograms in the age specific fecundity figures had fish with fecundity estimates of less than 2K. When you sub-set the data based on reproductive values the median eggs-per-female by age will increase, so the potential egg deposition by site will increase, which should drive down the egg-to-fry survival rates.

As I said at the beginning, I’m still wrapping my head around this IPM and have limited experience w/modeling and R code which makes it difficult for me to comment. I am however the person that knows the LCR chum data set’s quirks and limitations best. If you think I’m on the right track with what I’ve talked about above but haven’t been clear enough, or might have insight into something else you’ve noticed that’s “off”, I’m open to a call to talk through things in more detail.

I have more questions, but I’ll wait on those until I see the effects of the changes I suggested above. Truthfully, I can’t wait on one. When your predicting smolt abundance, which I’m guessing will influence forecasting returns, is all spawning habitat being considered equal? We have data that suggest it shouldn’t be in the Grays basin, unsure how this is being handled with I-205 mainstem Columbia River spawner sites and the near Bonneville populations (mainstem and trib spawner populations).

Hi @Hillsont, welcome to GitHub and thanks for weighing in! This kind of detailed insight into the natural history and the data is super helpful. Sorry it's taken me a little while to absorb all of your comments, and sorry the description of the model and analysis isn't more transparent and human-readable yet. I'm working on that, but at the same time still actively iterating on the code and results themselves.

I’ll start with the easy ones. You mention that sex ratio is way off 50:50 in some instances. I’m guessing these sites are primarily Duncan and Hamilton Spring Channel and I likely know the reason.

Good call -- those are indeed the most extreme cases, though not the only ones. What do you think is the reason?

In the April 4 message you say “Interestingly, the four populations in the Gorge_MS group are much less synchronous than you might expect if they were really all highly connected or even quasi-panmictic. That could be one reason why the models struggled to fit the 8-population grouping.” I’m assuming those four are Ives, Horsetail, Multnomah, and St Cloud. We see a fair amount of movement of fish between Horsetail, Multnomah, and St Cloud as a group and less between that group and Ives. Also, flow (Bonneville tailwater elevation) in some years can play a big part in spawner distribution. While Ives has a decent amount of spawning areas available at low tailwater, the other three are really limited at low tailwater (typical at the start of the spawning season) and prolonged periods of low tailwater and rainfall (important to get usage at St Cloud) can definitely shift fish around. Prolonged periods of low tailwater combined with low rainfall also impact spawner distribution between mainstem sites and tribs (2019 will be a great example).

Thanks, that makes sense. Just eyeballing the spawner time series, Horsetail and Multnomah do seem to be the most synchronous, although we could formally quantify this by looking at cross-correlations among the estimated states. Of course synchrony is just a proxy for dispersal, which is not explicitly modeled here. That's one of the things @kalebentley, Thomas and I have talked about including in the next phase of model development.

From the April 6 exchange “Are we eventually going to include hatchery pops? How ? Yes, we'd hoped to do that. As the above suggests, it's more complicated than I originally envisioned, especially because some locations (e.g., Duncan Channel) have characteristics of both hatcheries (broodstock intentionally transferred there) and natural populations (spawning occurs naturally; fry releases not directly quantified). This will bear more discussion for sure, in a separate issue.” I’m a bit confused by this statement, maybe it’s just terminology, Duncan Channel is a complicated site. We have both translocated adults from mainstem spawning sites and adults trapped at the mouth of Duncan Creek and transported into the spawning channel. What has me confused is it seems your treating these two groups separately, which shouldn’t be the case. Regardless of source (mainstem or trap), all adults are released above monitoring weirs in the spawning channels and they are mixed together in some year & channel combinations. That’s why the statement “(spawning occurs naturally; fry releases not directly quantified)” causes me to pause, fry production from the channels is a mix of both adult sources. It’s actually more complicated than that but I can’t remember if your using combined channel fry production or channel specific fry production (did the channel receive only translocated adults (green females only) or a mix of Duncan trap and translocated adults (would likely include partial spawned females)). Which value your using would dictate what mix of adults (mainstem and trap combined or mainstem only) produced the fry.

I think you may have hit on something important here, but I'm still having a hard time wrapping my head around it. Duncan is definitely complicated; it was the hardest site for me to understand, in terms of both the system itself and what to do with the data I was given. Let me start by briefly explaining how the pre-existing models in salmonIPM handle hatchery spawners, and how I tried to accommodate Duncan within that paradigm. In general, translocations of adults enter into salmonIPM models in two ways:

Broodstock removal. Some (known) number of natural-origin adults returning to a given population in a given year may be subtracted for broodstock; they are counted as recruits from the corresponding brood years, but not as spawners contributing to the next cohort of natural production.
Hatchery-origin spawners reproducing naturally. salmonIPM does not (yet!) explicitly model hatchery operations, i.e. the number of juveniles deliberately released (this is what I meant by "fry releases directly quantified") and their eventual fates. Instead, the origin-composition data are used to estimate p_HOS independently for each year in which hatchery-origin spawners are known or expected to be present. They are counted as contributing to the natural production, but not as recruits from previous brood years.

This simple framework has sufficed for the case studies I've worked on previously, but it doesn't allow translocations of natural-origin adults from one population to another. For Duncan Creek, the spawner data and BioData indicate three dispositions (Duncan Creek, Duncan Channel, and Duncan Hatchery) and the BioData indicate four origins (natural spawner, Duncan Channel, Duncan Hatchery, and Lewis Hatchery). The juvenile data include locations Duncan Channel (the sum of Duncan North and Duncan South) as well as Duncan Hatchery (but we're not modeling hatchery fry releases for now). After talking this over with @kalebentley, we came up with an admittedly hacky workaround: treat Duncan Channel as a "hatchery", in the sense that

Natural-origin spawners returning to Duncan Creek that are disposed to Duncan Channel are counted as broodstock removal.
Spawners born in Duncan Channel that return to Duncan Creek are included in the estimate of p_HOS.
The dynamics of spawners in Duncan Channel itself are not explicitly modeled (the spawner data doesn't include Duncan Channel as a location, so this seemed somewhat inevitable), BUT...
Juveniles outmigrating from Duncan Channel represent all naturally produced offspring of spawners that returned to Duncan Creek.

What I'm realizing now (I think, tell me if I've got this right) is that (4) is a fatally flawed assumption because the spawners in Duncan Channel include not just those that returned to Duncan Creek, but also some translocated in from mainstem populations. Oops! That wasn't clear to me, sorry. In fact, I'm not entirely sure that I see where this shows up in the data, since BioData includes Duncan Channel as an origin but not as a Location.Reach. If I'm understanding this correctly, you are absolutely right that this would explain a lot of the weirdness we're seeing, specifically the difficulty in fitting the smolt and spawner data for Duncan Creek and the crazy high egg-to-fry survival (at least for that population, and perhaps overall via the hyperdistribution) as the model tries to account for all the smolts produced using a subset of the spawners. What to do about it is another question.

Reproductive effort is the green egg mass weight (g) / female whole body weight (g). We use a reproductive effort value of 16% or greater as a cut off to identify females that likely had spawned in the wild before being collected as brood (based off work Steve Schroder did with Puget Sound chum salmon). When we generated potential egg deposition values at the Duncan Channels to estimate egg-to-fry survival we only use data from hatchery spawned females with > or = to 16% reproductive effort values (assumption is that egg-per-female at spawning = fecundity when reproductive effort meets threshold value). I was pretty sure all eggs-per-female data was being used when I saw the histograms in the age specific fecundity figures had fish with fecundity estimates of less than 2K. When you sub-set the data based on reproductive values the median eggs-per-female by age will increase, so the potential egg deposition by site will increase, which should drive down the egg-to-fry survival rates.

Excellent, thanks. The meaning of reproductive effort wasn't made clear to me. This will be very easy to do.

When your predicting smolt abundance, which I’m guessing will influence forecasting returns, is all spawning habitat being considered equal? We have data that suggest it shouldn’t be in the Grays basin, unsure how this is being handled with I-205 mainstem Columbia River spawner sites and the near Bonneville populations (mainstem and trib spawner populations).

I'm not totally sure I know what you mean by considering all spawning habitat equal, but I think this relates to the "capacity" parameter (Emax in the fully stage-structured model). In general, capacity is modeled as a random effect across populations (there's an overall mean and variance at the ESU level, and populations vary around that) which is estimated from the data along with all the other parameters. The observed population dynamics themselves tell us something about what the most plausible capacities are, even in the absence of any habitat data. However, habitat data -- which we might think of as quantity and quality -- can help inform / constrain the capacities. At the simplest level, even a crude estimate of spawning habitat quantity for each population will make the capacities more comparable by expressing them in units of eggs/km (or eggs/ha) rather than eggs. @kalebentley has been working on this; I'm not sure of the status of that effort. Habitat quality, aka environmental covariates, could help to further refine things, and we've talked about including that in the next phase of model-building.

Again, thanks for lending your time and insight to this discussion; it's very helpful. I think we're closer to understanding some of the nagging questions about this model and (hopefully) figuring out what to do about them.

Hi @Hillsont, welcome to GitHub and thanks for weighing in! This kind of detailed insight into the natural history and the data is super helpful. Sorry it's taken me a little while to absorb all of your comments, and sorry the description of the model and analysis isn't more transparent and human-readable yet. I'm working on that, but at the same time still actively iterating on the code and results themselves.

@ebuhle, please don’t take my comments before as criticism of transparency or readability. They were intended to let you know my skill level related to R code and modeling.

I’ll start with the easy ones. You mention that sex ratio is way off 50:50 in some instances. I’m guessing these sites are primarily Duncan and Hamilton Spring Channel and I likely know the reason.

Good call -- those are indeed the most extreme cases, though not the only ones. What do you think is the reason?

In almost all years Duncan Creek has had an adult trap at the mouth and any chum that volunteer to the trap are taken to the spawning channel. This can, and has, resulted in skewed sex ratios above the monitoring weirs (I’ll get into more about how Duncan channel is operated later). I believe some of the extreme ratios your seeing at Duncan also are related to the model not including translocated adults from mainstem spawning sites. I went back and looked at total males & females released above the monitoring weirs and we never had % females close to zero or 100%. Hamilton Springs has also had a weir & trap at the mouth since 2013. The weir wasn’t “fish tight” in the first couple of seasons but once we made it fish tight we noticed the sex ratio of recovered carcs leaned heavy to males. Our assumption was that males are more likely to move around between spawning sites looking for mates and once we made the weir fish tight they’d enter looking, but couldn’t leave.

This sex data is collected in two ways, either through carcass recoveries (Grays, WF Grays, CJ, Hamilton Springs, Hamilton & Hardy creeks), live seining (Cascade MS, St. Cloud, Multnomah, Horsetail, and Ives), or a combination of live trap and translocated adults captured via seining (Duncan channels). We don’t believe any of these methods are currently biased towards sex. First couple of years (2002-03) seining data were likely biased towards males due to the type of net they used. Th adults we’re sampling are close to spawning, or have already spawned, and it’s pretty easy to tell the sex of a chum salmon at this point, so I don’t think it’s observation error on the samplers part.

Low sample size may be a reason for some of the year & site combos having skewed ratios. I can remember some years for St Cloud, Horestail and Hardy Creek where we’d only capture or sample 1-5 adults.

In the April 4 message you say “Interestingly, the four populations in the Gorge_MS group are much less synchronous than you might expect if they were really all highly connected or even quasi-panmictic. That could be one reason why the models struggled to fit the 8-population grouping.” I’m assuming those four are Ives, Horsetail, Multnomah, and St Cloud. We see a fair amount of movement of fish between Horsetail, Multnomah, and St Cloud as a group and less between that group and Ives. Also, flow (Bonneville tailwater elevation) in some years can play a big part in spawner distribution. While Ives has a decent amount of spawning areas available at low tailwater, the other three are really limited at low tailwater (typical at the start of the spawning season) and prolonged periods of low tailwater and rainfall (important to get usage at St Cloud) can definitely shift fish around. Prolonged periods of low tailwater combined with low rainfall also impact spawner distribution between mainstem sites and tribs (2019 will be a great example).

Thanks, that makes sense. Just eyeballing the spawner time series, Horsetail and Multnomah do seem to be the most synchronous, although we could formally quantify this by looking at cross-correlations among the estimated states. Of course synchrony is just a proxy for dispersal, which is not explicitly modeled here. That's one of the things @kalebentley, Thomas and I have talked about including in the next phase of model development.

From the April 6 exchange “Are we eventually going to include hatchery pops? How ? Yes, we'd hoped to do that. As the above suggests, it's more complicated than I originally envisioned, especially because some locations (e.g., Duncan Channel) have characteristics of both hatcheries (broodstock intentionally transferred there) and natural populations (spawning occurs naturally; fry releases not directly quantified). This will bear more discussion for sure, in a separate issue.” I’m a bit confused by this statement, maybe it’s just terminology, Duncan Channel is a complicated site. We have both translocated adults from mainstem spawning sites and adults trapped at the mouth of Duncan Creek and transported into the spawning channel. What has me confused is it seems your treating these two groups separately, which shouldn’t be the case. Regardless of source (mainstem or trap), all adults are released above monitoring weirs in the spawning channels and they are mixed together in some year & channel combinations. That’s why the statement “(spawning occurs naturally; fry releases not directly quantified)” causes me to pause, fry production from the channels is a mix of both adult sources. It’s actually more complicated than that but I can’t remember if your using combined channel fry production or channel specific fry production (did the channel receive only translocated adults (green females only) or a mix of Duncan trap and translocated adults (would likely include partial spawned females)). Which value your using would dictate what mix of adults (mainstem and trap combined or mainstem only) produced the fry.

I think you may have hit on something important here, but I'm still having a hard time wrapping my head around it. Duncan is definitely complicated; it was the hardest site for me to understand, in terms of both the system itself and what to do with the data I was given. Let me start by briefly explaining how the pre-existing models in salmonIPM handle hatchery spawners, and how I tried to accommodate Duncan within that paradigm. In general, translocations of adults enter into salmonIPM models in two ways:

Broodstock removal. Some (known) number of natural-origin adults returning to a given population in a given year may be subtracted for broodstock; they are counted as recruits from the corresponding brood years, but not as spawners contributing to the next cohort of natural production.

Hatchery-origin spawners reproducing naturally. salmonIPM does not (yet!) explicitly model hatchery operations, i.e. the number of juveniles deliberately released (this is what I meant by "fry releases directly quantified") and their eventual fates. Instead, the origin-composition data are used to estimate p_HOS independently for each year in which hatchery-origin spawners are known or expected to be present. They are counted as contributing to the natural production, but not as recruits from previous brood years.

This simple framework has sufficed for the case studies I've worked on previously, but it doesn't allow translocations of natural-origin adults from one population to another. For Duncan Creek, the spawner data and BioData indicate three dispositions (Duncan Creek, Duncan Channel, and Duncan Hatchery) and the BioData indicate four origins (natural spawner, Duncan Channel, Duncan Hatchery, and Lewis Hatchery). The juvenile data include locations Duncan Channel (the sum of Duncan North and Duncan South) as well as Duncan Hatchery (but we're not modeling hatchery fry releases for now). After talking this over with @kalebentley, we came up with an admittedly hacky workaround: treat Duncan Channel as a "hatchery", in the sense that

Natural-origin spawners returning to Duncan Creek that are disposed to Duncan Channel are counted as broodstock removal.

Spawners born in Duncan Channel that return to Duncan Creek are included in the estimate of p_HOS.

The dynamics of spawners in Duncan Channel itself are not explicitly modeled (the spawner data doesn't include Duncan Channel as a location, so this seemed somewhat inevitable), BUT...

Juveniles outmigrating from Duncan Channel represent all naturally produced offspring of spawners that returned to Duncan Creek.

What I'm realizing now (I think, tell me if I've got this right) is that (4) is a fatally flawed assumption because the spawners in Duncan Channel include not just those that returned to Duncan Creek, but also some translocated in from mainstem populations. Oops! That wasn't clear to me, sorry. In fact, I'm not entirely sure that I see where this shows up in the data, since BioData includes Duncan Channel as an origin but not as a Location.Reach. If I'm understanding this correctly, you are absolutely right that this would explain a lot of the weirdness we're seeing, specifically the difficulty in fitting the smolt and spawner data for Duncan Creek and the crazy high egg-to-fry survival (at least for that population, and perhaps overall via the hyperdistribution) as the model tries to account for all the smolts produced using a subset of the spawners. What to do about it is another question.

The simplest way to work through this would on a big white board where we could diagram this all out and see how it all fits together. Since that’s not possible, thanks COVID, I’ll try and layout what happens at Duncan so you can determine how the parts need to fit within the model. There are some “odd” years (2-3 years when there was no trap at the mouth), but what I’ll describe covers the vast majority of the seasons.

Duncan can be broken down into three main parts/ reaches: the adult trap at the mouth, the spawning channel above the monitoring weirs, and Duncan Creek proper (includes Duncan Creek above the adult trap at the mouth and any parts of the spawning channels below the monitoring weirs). Additionally, the spawning channel is divided into two sections (North and South channel). Sheet pile weirs with adult screens/ grates (monitoring weirs) separate the North and South channels preventing adults released into either channel from leaving or mixing (there are exceptions but rare enough to not matter at this point). The monitoring weirs also prevent any fish from joining the population above the weirs in those years when we didn’t have an adult trap at the mouth. Duncan was set up to evaluate re-introduction strategies (natural straying, adults produced from translocated adults released above the monitoring weirs (spawning naturally in channels producing fry), and adults produced from hatchery-origin fry releases, so it was important to keep spawning adults separated. Two of these methods are evaluated using returning adults from fry produced (NORs from spawning channel or HORs from hatchery releases), the third is evaluated by looking at stray rates (non channel- or hatchery-origin adults recruiting to Duncan Creek.

There are three sources for adults released into the channels above the monitoring weirs: the Duncan adult trap, the Hamilton Springs v-weir (BY 2013 forward), and translocated from mainstem spawning sites (captured via seining). Adults from all three sources contribute to fry produced from the channels, measured via weir and live-box traps operated at each monitoring weir. Any fry produced from adults that spawned outside the channels in Duncan (very few, in just a couple of years when no trap at the mouth was operated) were not documented.

Chum salmon captured at the Duncan adult trap can have four dispositions: North channel, South channel, hatchery, or downstream (released back into the Columbia River, status could be live or mortality), 99% are taken to one of the two spawning channels. Adults captured at Duncan Trap could be strays (natural-origin) or project (channel- or hatchery-origin) adults.

Chum salmon captured at the Hamilton Springs v-weir also can have four dispositions: North channel, South channel, hatchery, or upstream (tagged and released into spring channel to aid with pop estimate). As is the case at the Duncan adult trap, adults collected here and taken to the Duncan channels, or for hatchery broodstock, could be natural- or project- (channel or hatchery) origin adults.

I think we all understand translocated adults so I won’t say much about them. From what I can tell we’re treating them correctly: credited as recruits from previous BYs based on age and origin (natural, channel, or hatchery) for productivity estimates but not included (removed for broodstock to either Duncan channels or hatchery program) as spawners for future recruits at the sites they were collected from. This is getting father into the weeds and a bit off topic, but I believe the intent is to use the results of the Parental Based Tagging analysis for estimating dispersal rates eventually which will help firm up spawner site specific productivity. Until then maybe we should be doing some lumping of spawning sites when estimating productivity based on adult returns?

Now I need to bring up another quirk at Duncan. One of the project’s annual goals is to measure egg-to-fry survival at the spawning channels. This not only gives us a productivity metric for adults using artificial spawning channels, it is used to determine if channel maintenance is needed (i.e. gravel cleaning). If we wanted to measure egg-to-fry survival that meant only releasing green (firm belly’s indicating un-ripe eggs and no fin erosion to indicate redd digging actions) females above the monitoring weirs. This wasn’t to hard to accomplish in the early years when returns were high, we had no project origin adults returning yet, and no adult trap at Duncan. This all changed in the mid-2000s. I’m going to skip detailing all the reasons for why we made this decision and just get to what’s important for the model. Beginning in BY 2006, one of the two channels would be designated to only receive green females (captured via seining at mainstem sites) and the other for all adults captured at the adult trap plus green or partial females collected at mainstem sites. We would swap which channel got which treatment annually, but not always, so we could continue to get information on both channels performance and need for maintenance. I see this being dealt with two ways. We could only use adults and fry produced from the channel that received green girls each year for egg-to-fry survival rates or have the model estimate the number of eggs deposited in both channels based on fecundity by age estimates and use the combined channel fry estimate. I think the latter is what we’re doing now. With either approach we still have the issue of translocated adults not being accounted for.

Hopefully this helps clear and not muddied the water more. Another thought I had since Duncan is so complex, and doesn’t fit the IPM well yet, would be to remove its influence. We could just use Hamilton Springs, Grays and CJ adult returns and fry estimates to generate egg-to-fry survival rates. Since none of these sites include adding in translocated adults, it would be cleaner until how to handle Duncan is figured out.

Reproductive effort is the green egg mass weight (g) / female whole body weight (g). We use a reproductive effort value of 16% or greater as a cut off to identify females that likely had spawned in the wild before being collected as brood (based off work Steve Schroder did with Puget Sound chum salmon). When we generated potential egg deposition values at the Duncan Channels to estimate egg-to-fry survival we only use data from hatchery spawned females with > or = to 16% reproductive effort values (assumption is that egg-per-female at spawning = fecundity when reproductive effort meets threshold value). I was pretty sure all eggs-per-female data was being used when I saw the histograms in the age specific fecundity figures had fish with fecundity estimates of less than 2K. When you sub-set the data based on reproductive values the median eggs-per-female by age will increase, so the potential egg deposition by site will increase, which should drive down the egg-to-fry survival rates.

Excellent, thanks. The meaning of reproductive effort wasn't made clear to me. This will be very easy to do.

Cool. I'm sure once the eggs-per-female data is stratified using reproductive effort, the other model outputs that rely on it will look more realistic.

When your predicting smolt abundance, which I’m guessing will influence forecasting returns, is all spawning habitat being considered equal? We have data that suggest it shouldn’t be in the Grays basin, unsure how this is being handled with I-205 mainstem Columbia River spawner sites and the near Bonneville populations (mainstem and trib spawner populations).

I'm not totally sure I know what you mean by considering all spawning habitat equal, but I think this relates to the "capacity" parameter (Emax in the fully stage-structured model). In general, capacity is modeled as a random effect across populations (there's an overall mean and variance at the ESU level, and populations vary around that) which is estimated from the data along with all the other parameters. The observed population dynamics themselves tell us something about what the most plausible capacities are, even in the absence of any habitat data. However, habitat data -- which we might think of as quantity and quality -- can help inform / constrain the capacities. At the simplest level, even a crude estimate of spawning habitat quantity for each population will make the capacities more comparable by expressing them in units of eggs/km (or eggs/ha) rather than eggs. @kalebentley has been working on this; I'm not sure of the status of that effort. Habitat quality, aka environmental covariates, could help to further refine things, and we've talked about including that in the next phase of model-building.

Eric, what made me ask about all habitat being treated equal was the forecast, modeled smolt abundance (Figure 3), and the 5-year predicted spawner data (Figure 6). I think for chum salmon the quality of habitat is very important for productivity. To be productive, they rely on high quality off-channel ground water influenced spawning habitat. I’ll use the Grays basin as an example. The Crazy Johnson (CJ) spawning area is a protected off-main channel spawning area with loads of groundwater influence. Our adult and juvenile monitoring data suggest this area has high productivity (egg-to-fry survival rates). The mainstem Grays and WF Grays are not protected off-channel spawning areas and that’s reflected in lower egg-to-fry survival rates based on our adult and juvenile monitoring data. Frequency and magnitude of winter freshest being the driver on annual productivity in these areas. While we don’t have the monitoring data to back it up, we believe the mainstem Columbia River spawning areas have lower productivity rates compared to the protected off-channel spawning sites in that area (Duncan and Hamilton channels). There are published studies that we’re basing out assumptions on.

My concern is that we’re assigning unrealistic productivity values to areas, i.e. using Duncan and Hamilton Springs egg-to-fry survival rates for mainstem Columbia River (Ives, Horsetail, Multnomah, St Cloud, and Cascade MS), Hardy and Hamilton creek spawners. The same could be said for Grays basin spawning areas if area/ reach specific rates were not used.

Again, thanks for lending your time and insight to this discussion; it's very helpful. I think we're closer to understanding some of the nagging questions about this model and (hopefully) figuring out what to do about them.

I’m all about figuring this stuff out. It’s really exciting to see all the monitoring data collected under this project I participated in and oversaw for 17 years being put together under this IPM framework. Unfortunately, all I can do at this point is to bring up things I see as not making sense. Please don’t take any of my comments as a negative.

OK, in light of @Hillsont's extremely helpful post above and my long phone call with @kalebentley, I went back and overhauled the data-wrangling code / logic. The key insight was that, for spawner_data and bio_data, "populations" are defined by disposition rather than location -- that is, all spawners that ended up at a given site, regardless of the location to which they initially returned. From there it's "just" a matter of properly accounting for broodstock removal, spawners of nonlocal origin that should not be counted as local recruitment, and matching up juvenile data with the appropriate spawning areas. I say "just" in scare quotes because this is actually a nontrivial data-wrangling problem, with all sorts of tricky little carve-outs and edge cases that are hard to keep track of and easy to screw up. Duncan Channel / Creek is of course the poster child, but there are lots of other instances.

Below is a synopsis of the main changes and the new assumptions they entail. You can find more detail in the comments on the script.

As noted above, populations are defined by the disposition column in spawner_data and bio_data. Specifically, S_obs and the n_age_obs and n_HW_obs columns are created by aggregating at this level. The juv_data only has a location column, so this was used to match the disposition in the other two data sets. Ultimately, all hatchery dispositions were tossed out; Duncan_Channel was retained instead of Duncan_Creek (see below); and Grays_MS was merged with Grays_WF (see below).
Broodstock take, on the other hand, was defined by location, i.e., B_take_obs is the sum of all spawners returning to a given location that were taken to a different disposition, whether that was a hatchery or spawning channel.
Since the current models don't have a way to explicitly represent deliberate translocations of spawners into a population (only their removal as broodstock), the only way to avoid counting translocated spawners as local recruits is to classify them as "hatchery-origin". That is, n_W_obs and n_H_obs are constructed from bio_data by labeling any spawner that is of known hatchery (or otherwise nonlocal) origin OR that has a location different from its disposition as "H". Thus the interpretation of the parameter p_HOS will actually be "proportion of hatchery- or other known nonlocal-origin spawners". This is a minimum estimate, because of course we don't know how many fish with origin=="Natural_spawner" and location==disposition are in fact strays from other populations.
- Exception: Fish returning to location == "Duncan_Creek" that are of origin %in% c("Duncan_Channel", "Natural_spawner") are considered to be local recruitment from Duncan Channel, so if they have disposition == "Duncan_Channel" they are counted as "W". Only a handful of fish (zero in most years) had disposition == "Duncan_Creek", so "Duncan_Channel" is now considered the population and "Duncan_Creek" has been dropped.
- In future versions of the chum IPM, we could disaggregate hatchery- and nonlocal-origin spawners and restore the usual interpretation of p_HOS in one of two ways:
- Define a new compositional data type c(n_local_obs, n_nonlocal_obs) based on bio_data and use it to estimate a new parameter p_nonlocal that would function similarly to p_HOS, i.e., inflate the NOR to account for nonlocal-origin spawners that "show up" on the spawning grounds.
- Define a new data type S_add_obs based on spawner_data, i.e., the total number of spawners with location != disposition, summed by disposition. S_add_obs would function somewhat like an inverse B_take_obs; the values (which are basically known without error) would be added directly to the NOR. This seems like the better, more straightforward option. Either way, we'll have to be careful to properly account for true hatchery-origin spawners, some of which may be among the spawners translocated in.
For juvenile data, as I mentioned over here, I'm taking location == "Duncan_Channel" to be the total fry outmigration from the Duncan Channel(s), regarded as a single population, and ignoring "Duncan_North" and "Duncan_South".
The Grays River system is another tricky special carve-out, based on discussion with @kalebentley. Juvenile data with location=="Grays_MS" actually represents the summed production from three "populations" in the spawner_data and bio_data ("Grays_MS", "Grays_WF", and "Grays_CJ"), so it cannot be matched to any one of them. Further complicating things, fry from Crazy Johnson Creek are double-counted, in both location == "Grays_CJ" and as part of location == "Grays_MS". We came up with the following, admittedly hacky workaround:
- Adult data (spawner abundance and compositional samples) for "Grays_MS" and "Grays_WF" are pooled into a single "population", "Grays_MSWF". The problem then becomes how to characterize the prior on the sum of S_obs in each year. We are assuming each unique S_obs prior is lognormal, but the lognormal is not closed under addition; indeed, there is no closed form for the sum of lognormals. Instead, I approximated the sum by adding independent Monte Carlo samples from the two priors. Assuming the sum is lognormal -- which is technically impossible, but a pretty good approximation when the CVs are as small as they are in this case -- I used method of moments to estimate S_obs and tau_S_obs. There is one year (2009) when S_obs is missing for "Grays_MS" but not for "Grays_WF", so we lose that data point.
- In order to keep Crazy Johnson as a distinct population with its own spawner and smolt time series, we have to subtract "Grays_CJ" smolts from "Grays_MS" (assuming zero mortality between the Crazy Johnson trap and the mainstem trap). I used a Monte Carlo hack analogous to the one described above for S_obs, but in this case taking the difference to be lognormal. The approximation is more dubious here, especially in some years where the resulting log(M_obs) is left-skewed. Also, smolt data start in 2008 for "Grays_MS" but not until 2012 for "Grays_CJ", so this procedure costs us four years of data.
- For all the reasons noted, this solution is not ideal; it illustrates many of the drawbacks of a piecemeal approach to parameterizing LCMs. In the spirit of IPMs, a better approach would be to make the model outputs match the data rather than vice versa. We could do that by keeping "Grays_MS", "Grays_WF", and "Grays_CJ" as separate populations and summing states as appropriate (e.g., the predicted smolt abundance for "Grays_MS" would be the sum of M across all three pops). I actually think this wouldn't be too painful to implement, although like the local / nonlocal approaches discussed above, it would break backward compatibility of fish_data with the simpler salmonIPM models (maybe they've served their purpose, and that's fine). It also wouldn't address the likely high dispersal among the three Grays River populations, but of course the same could be said for other areas, hence the motivation to model straying.
Last and by far the least effort, fecundity_data is now filtered for reproductive_effort >= 16.

I'm re-fitting the models with this revised data set. So far so good...

For all the reasons noted, this solution is not ideal; it illustrates many of the drawbacks of a piecemeal approach to parameterizing LCMs. In the spirit of IPMs, a better approach would be to make the model outputs match the data rather than vice versa. We could do that by keeping "Grays_MS", "Grays_WF", and "Grays_CJ" as separate populations and summing states as appropriate (e.g., the predicted smolt abundance for "Grays_MS" would be the sum of M across all three pops). I actually think this wouldn't be too painful to implement, although like the local / nonlocal approaches discussed above, it would break backward compatibility of fish_data with the simpler salmonIPM models (maybe they've served their purpose, and that's fine). It also wouldn't address the likely high dispersal among the three Grays River populations, but of course the same could be said for other areas, hence the motivation to model straying.

Well, I got impatient so I went ahead and did this. Surprisingly simple to implement and gives comparable results to the hacky data-munging way, which reassured me that I did it right. Fits to the data (smolts, spawners, even age comp) are much, much better than before, especially for Duncan Channel (formerly Creek). But egg-to-fry survival, while a little lower, is still way too high:

I'm thinking again about @tbuehrens's suggestion to put the density-dependence in egg-to-fry survival instead of egg deposition. I think it's worth trying. I'll make another issue for that.

Hey @ebuhle,

First, sorry for the delay in responding to your most recent post - I was off work all last week.

Second, I'm going to have to read through your notes a few times to totally wrap my head around the changes you made and the implications (specifically, what to do with the Grays River dataset).

Lastly, I wanted to quickly ask you about the updated results you posted and, specifically, the egg deposition vs. spawners plot. @Hillsont actually brought this to my attention. It seems like the predicted egg deposition is too low - at least based on some back-of-the-napkin calculations. For example, with 1,500 spawners, a 50:50 sex ratio, and say 2,700 eggs/female, you would expect ~2M eggs to be deposited. However, the "hyper-mean" appears to be closer to 1M. I am assuming this "deviation" is because we chose (at least initially) to structure the model so that the density-dependent (B-H function) life stage occurs between adults and eggs deposited as opposed to from eggs to fry/smolts. Thus, this is why the resulting estimates of egg-to-fry survival seem too high relative to what we would expect given that our expectations are essentially based on the alternative parameterization (i.e., density dependence occurs after deposition). Put another way, how we define freshwater survival and comparing it to other "estimates" obviously matters. This potential side effect didn't occur to me during our previous conversation when we decided how to structure the density-dependent life stage in freshwater.

Is this your interpretation of what could be occurring or am I totally misunderstanding?

ebuhle / LCRchumIPM

Initial IPM fits and data questions #3