adityavarre
commented
2 years ago You can guarantee that the left part is ≥ 0 by redoing the same calculations for $ y - x = - (\epsilon) e_i $. for some small $ \epsilon > 0 $. This was made clear in the exercise session; we will update the solutions to reflect the same.
In the proof, I found that after dividing both sides by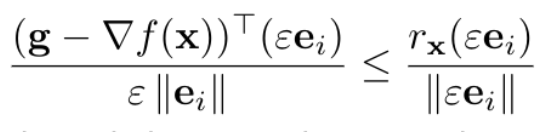
we can only conclude that the left part is ≤ 0 (since there is no guarantee that it is ≥ 0 to conclude that it is indeed 0)
I found another approach on Mathematics Stack Exchange which seem to be clearer. The fact that the LHS ≤ 0 for all e_i can still be used to come to conclusion (as we can combine the e_i component to get z in the Stack Exchange proof). But my main point is that we can't conclude LHS = 0