Can you please share your code? It is difficult to know what could be going on without seeing it. Also, please do not post screenshots of code into issues / discussions on GitHub. It's not searchable and it's more difficult to read.
Open RicardoSendrea07 opened 2 years ago
Can you please share your code? It is difficult to know what could be going on without seeing it. Also, please do not post screenshots of code into issues / discussions on GitHub. It's not searchable and it's more difficult to read.
Thank you for your feedback! I am expecting the mode overlap metric to improve as I move closer to the source, due to a decrease in attenuation.
Please find below the code for this case:
import numpy as np
import ceviche
from ceviche import fdfd_ez, jacobian
from ceviche.modes import insert_mode
import collections
import matplotlib.pylab as plt
import autograd.numpy as npa
def viz_sim(omega, dl, epsr, source, slices=[]):
"""Solve and visualize a simulation with permittivity 'epsr'
"""
simulation = fdfd_ez(omega, dl, epsr, [Npml, Npml])
Hx, Hy, Ez = simulation.solve(source)
fig, ax = plt.subplots(1, 2, constrained_layout=True, figsize=(6,3))
ceviche.viz.real(Ez, outline=epsr, ax=ax[0], cbar=False)
for sl in slices:
ax[0].plot(sl.x*np.ones(len(sl.y)), sl.y, 'b-')
ceviche.viz.abs(epsr, ax=ax[1], cmap='Greys');
plt.show()
return (simulation, ax)
def mode_overlap(E1, E2):
"""Defines an overlap integral between the simulated field and desired field
"""
return npa.abs(npa.sum(npa.conj(E1)*E2))
''' Setup parameters '''
centerFreq = 200e12
C = 3e8 #Speed of light
lam = C / centerFreq # Lambda (without considering eps)
omega=2*np.pi*centerFreq # Angular frequency of the source in 1/s
dl = (1/30)*lam # Spatial resolution in meters
Nx_l = 10*lam
Nx=int(Nx_l/dl)+1 # Number of pixels in x-direction
Ny=int(Nx_l/dl)+1 # Number of pixels in y-direction
Npml=int(lam/dl)+1 # Number of pixels in the PMLs in each direction
epsr_min=1.0 # Minimum value of the relative permittivity
epsr_max=3.0 # Maximum value of the relative permittivity
space= int(0.25*lam / dl) #Space between the PMLs and the design region (in pixels)
wg_width_l = lam / 2 #6 mm
wg_width=int(wg_width_l / dl)+1 # Width of the waveguide (in pixels)
space_slice = 12
Slice = collections.namedtuple('Slice', 'x y')
#Setup the straight waveguide
runSteps = Nx - 2*Npml + 2
centerPosition = int(Ny / 2)
epsr = epsr_min*np.ones((Nx, Ny))
epsr[:, centerPosition-int(wg_width/2):centerPosition+int(wg_width/2)] = epsr_max
#Setup slices
input_slice = Slice(x=np.array(Npml+1), y=np.arange(int(Ny/2-wg_width/2-space_slice), int(Ny/2+wg_width/2+space_slice)))
output_slice = Slice(x=np.array(Nx-Npml-1), y=np.arange(int(Ny/2-wg_width/2-space_slice), int(Ny/2+wg_width/2+space_slice)))
#Setup source
source = insert_mode(omega, dl,input_slice.x, input_slice.y, epsr, m=1)
#Simulate initial device
simulation, ax = viz_sim(omega, dl, epsr, source, slices=[input_slice, output_slice])
#Get E-Field
_, _, Ez = simulation.solve(source)
#Find Modeoverlap change across the waveguide
obj = np.zeros((runSteps,))
for i in range(runSteps):
#Setup output probe
probes = insert_mode(omega, dl, output_slice.x - i, output_slice.y, epsr, m=1)
#Get coupling eff.
obj[i] = 10*np.log10(mode_overlap(Ez, probes))
if mode_overlap(Ez, source) == 0:
obj[i] = -60
#Visualize performance
plt.figure()
plt.plot(np.linspace(0, runSteps, runSteps), obj, '--k', lw = 2)
plt.plot(np.linspace(0, runSteps, runSteps), obj, 'bs', ms = 1)
plt.xlim([0, runSteps])
plt.ylim([-60, 0])
plt.grid('on')Dear RicardoSendrea07, when you calculate the value of obj[i], you use a calculated mode and a field "simulated". You cannot to make that. If you plot them separately, you will see that the two represent different quantities.
Thank you Dj1312,
I realize that these are two different components. Following the notebooks, I thought that the probe represented our 'desired' field quantity. Thus, in this straight case, at the probe, I expected the field to be very similar to the calculated one.
I would like to measure the coupling efficiency of a waveguide design. How can I use the mode_overlap function to do this appropriately?
@RicardoSendrea07 I think you are misunderstanding the simulation and the physics.
Why do you expect the mode overlap value to change with the position of the probe? The waveguide is lossless, so the flat curve that you observed is expected.
Also, the mode overlap value should not have units of dB, since it's not a ratio or a transmission. If you want to calculate a transmission over some length of waveguide, you need to calculate the overlap at two locations (e.g. one close to the source, and one further away from the source) and take their ratio.
Thank you @ianwilliamson,
Initially, I expected to observe some attenuation, but I was wrong as the system is lossless.
In that case, what exactly is the mode overlap value? I had understood it to be a similarity value between the desired and measured fields.
The overlap value is going to be proportional to the amplitude of the eigenmode propagating through that cross section of the simulation. I say proportional to because the function, as it's defined in your snippet above, is missing some scaling constants. For example, you could normalize the overlap calculation such that |overlap value|^2 == propagating power in the mode.
Part of the reason that I suggested normalizing the two different mode overlap values at different locations is to avoid this ambiguity in the units of the overlap value.
Okay, so the overlap will be proportional to the amplitude of the specified mode given
in: insert_mode(omega, dl,input_slice.x, input_slice.y, epsr, m=1) ?
If I wanted to track power transmission of a mode of a waveguide, would calculating the ratio of this normalized overlap value across two points work?
I realized an example of how I understood it should be done, using a straight waveguide across a frequency sweep as an example.
Example Waveguide:
 Transmission Results:
Transmission Results:

# -*- coding: utf-8 -*-
"""
Self contained approach - Power Transmission across Straight Waveguide
"""
import numpy as np
import ceviche
from ceviche import fdfd_ez
from ceviche.modes import insert_mode
import collections
import matplotlib.pylab as plt
import autograd.numpy as npa
def viz_sim(epsr, source, slices=[], i = 0, typePlot = 1, flags = [], plotVis = 0):
"""Solve and visualize a simulation with permittivity 'epsr'
"""
simulation = fdfd_ez(omega, dl, epsr, [Npml, Npml])
Hx, Hy, Ez = simulation.solve(source)
if plotVis == 0:
fig, ax = plt.subplots(1, 2, constrained_layout=True, figsize=(20,10))
ceviche.viz.real(Ez, outline=epsr, ax=ax[0], cbar=False)
ax[0].set_title('Ez field', fontsize=20)
ax[0].tick_params(axis="both", labelsize=15)
ax[0].locator_params(nbins=10)
for sl in slices:
ax[0].plot(sl.x*np.ones(len(sl.y)), sl.y, 'b-')
ceviche.viz.abs(epsr, ax=ax[1], cmap='Greys');
ax[1].set_title('Material Distribution',fontsize=20)
ax[1].tick_params(axis="both", labelsize=15)
ax[1].xaxis.set_visible(False)
ax[1].yaxis.set_visible(False)
ax[1].locator_params(nbins=10)
plt.show()
else:
ax = 1
return (simulation, ax)
def mode_overlap(E1, E2):
"""Defines an overlap integral between the simulated field and desired field
"""
return npa.abs(npa.sum(npa.conj(E1)*E2))**2
''' Setup the center sweep parameters '''
centerFreq = 200e12
C = 3e8 #Speed of light
lam = C / centerFreq # Lambda (without considering eps)
omega=2*np.pi*centerFreq # Angular frequency of the source in 1/s
dl = (1/30)*lam # Spatial resolution in meters
Nx_l = 10*lam
Nx=int(Nx_l/dl)+1 # Number of pixels in x-direction (114)
Ny=int(Nx_l/dl)+1 # Number of pixels in y-direction
Npml=int(lam/dl)+1 # Number of pixels in the PMLs in each direction (20)
epsr_min=1.0 # Minimum value of the relative permittivity
epsr_max=3.0 # Maximum value of the relative permittivity
space= int(0.25*lam / dl) #Space between the PMLs and the design region (in pixels)
wg_width_l = lam / 2 #6 mm
wg_width=int(wg_width_l / dl)+1 # Width of the waveguide (in pixels)
space_slice = 12
Slice = collections.namedtuple('Slice', 'x y')
#Setup the straight waveguide
runSteps = 201
freqSweep = np.linspace(1, 400, runSteps)*1e12
centerPosition = int(Ny / 2)
epsr = epsr_min*np.ones((Nx, Ny))
epsr[:, centerPosition-int(wg_width/2):centerPosition+int(wg_width/2)] = epsr_max
#Setup slices
input_slice = Slice(x=np.array(Npml+1), y=np.arange(int(Ny/2-wg_width/2-space_slice), int(Ny/2+wg_width/2+space_slice)))
output_slice = Slice(x=np.array(Nx-Npml-1), y=np.arange(int(Ny/2-wg_width/2-space_slice), int(Ny/2+wg_width/2+space_slice)))
#Find transmission across a freq. sweep
transmission = np.zeros((runSteps,), dtype = 'complex')
for i in range(runSteps):
#for i in range(10):
omega=2*np.pi*freqSweep[i] # Angular frequency of the source in 1/s
# Setup source
source = insert_mode(omega, dl, input_slice.x, input_slice.y, epsr, m=1)
# Simulate initial device
simulation, ax = viz_sim(epsr, source, slices=[input_slice, output_slice], i=0, typePlot= 1, flags = [], plotVis = 0)
#Get E-Field
_, _, Ez = simulation.solve(source)
probesOut = insert_mode(omega, dl, output_slice.x, output_slice.y, epsr, m=1)
probesIn = insert_mode(omega, dl, input_slice.x+1, input_slice.y, epsr, m=1)
refIn = mode_overlap(Ez[input_slice.x+1, input_slice.y], probesIn[input_slice.x+1, input_slice.y])
refOut = mode_overlap(Ez[output_slice.x, output_slice.y], probesOut[output_slice.x, output_slice.y])
transmission[i] = refOut / refIn
''' Visualize performance '''
plt.figure()
plt.plot(freqSweep*1e-12, 10*np.log10(transmission), '--b', lw = 4)
plt.plot(freqSweep*1e-12, 10*np.log10(transmission), 'rs', ms = 4)
plt.xlim([0, 400])
#plt.ylim([-60, 0])
plt.grid('on')Yeah this is the best way to do it. You can see from the field plot that the source is not perfectly injected into the waveguide. By normalizing using the amplitude of the waveguide mode right after the source, you're now really looking at what you want: the power transmission of that mode between the two measurement points.
@RicardoSendrea07 From looking at your field plot, it appears that your eigenmode source is diffracting a bit (energy propagating obliquely up and down from the waveguide). This indicates that your source may not extend far enough beyond the waveguide core. I would suggest increasing the extent of the source, as well as the probe slices, in the vertical direction.
Okay, great! Thank you @ianwilliamson and @momchilmm for the feedback! I appreciate you taking the time to answer my questions.
Lastly, this result led me to another question. When I insert a source along a cross-section, what is Ceviche doing exactly, is it placing a weighted combination of all the possible modes?
Currently, the cross-section my designed to support the fundamental mode (TM10) of a waveguide at 200THz. Following this equation:
f_c = ((3.0e8) / 2*np.pi) * np.sqrt((m*np.pi/a)**2 + (n*np.pi/b)**2)
, where a is the waveguide width, and b is assumed to be a/2 (although not represented in the 2D simulation). In this scenario, the TM10 is supported from 115THz to 230THz, which is where higher-order modes begin to propagate alongside it.
When I perform the frequency sweep, I’m expecting the source to be near zero where it is not supported, i.e., at the start of the frequency sweep. From the field plot of the inserted source at 1THz, the mode is not propagating in the waveguide, yet it's not zero.

To further push this point, I plotted the source maxima magnitude along the same frequency sweep. As can be seen from the graph, the source placed seems to oscillate (switch on/off) from a near-zero value to an amplitude of about 0.3 across the sweep. Why is this the case?

The code to generate this example:
# -*- coding: utf-8 -*-
"""
Self contained approach - Mode Magnitude over frequency
"""
import numpy as np
import ceviche
from ceviche import fdfd_ez, jacobian
from ceviche.modes import insert_mode
import collections
import matplotlib.pylab as plt
import autograd.numpy as npa
def viz_sim(epsr, source, slices=[], i = 0, typePlot = 1, flags = [], plotVis = 0):
"""Solve and visualize a simulation with permittivity 'epsr'
"""
simulation = fdfd_ez(omega, dl, epsr, [Npml, Npml])
Hx, Hy, Ez = simulation.solve(source)
if plotVis == 0:
fig, ax = plt.subplots(1, 2, constrained_layout=True, figsize=(20,10))
ceviche.viz.real(Ez, outline=epsr, ax=ax[0], cbar=False)
ax[0].set_title('Ez field', fontsize=20)
ax[0].tick_params(axis="both", labelsize=15)
ax[0].locator_params(nbins=10)
for sl in slices:
ax[0].plot(sl.x*np.ones(len(sl.y)), sl.y, 'b-')
ceviche.viz.abs(epsr, ax=ax[1], cmap='Greys');
ax[1].set_title('Material Distribution',fontsize=20)
ax[1].tick_params(axis="both", labelsize=15)
ax[1].xaxis.set_visible(False)
ax[1].yaxis.set_visible(False)
ax[1].locator_params(nbins=10)
plt.show()
else:
ax = 1
return (simulation, ax)
def mode_overlap(E1, E2):
"""Defines an overlap integral between the simulated field and desired field
"""
#Normalized
return npa.abs(npa.sum(npa.conj(E1)*E2))
''' Setup the center sweep parameters '''
centerFreq = 200e12
C = 3e8 #Speed of light
lam = C / centerFreq # Lambda (without considering eps)
omega=2*np.pi*centerFreq # Angular frequency of the source in 1/s
dl = (1/30)*lam # Spatial resolution in meters
Nx_l = 10*lam
Nx=int(Nx_l/dl)+1 # Number of pixels in x-direction (114)
Ny=int(Nx_l/dl)+1 # Number of pixels in y-direction
Npml=int(lam/dl)+1 # Number of pixels in the PMLs in each direction (20)
epsr_min=1.0 # Minimum value of the relative permittivity
epsr_max=3.0 # Maximum value of the relative permittivity
space= int(0.25*lam / dl) #Space between the PMLs and the design region (in pixels)
wg_width_l = lam / 2 #6 um
wg_width=int(wg_width_l / dl)+1 # Width of the waveguide (in pixels)
space_slice = 24
Slice = collections.namedtuple('Slice', 'x y')
#Setup the straight waveguide
runSteps = 51
freqSweep = np.linspace(1, 400, runSteps)*1e12
centerPosition = int(Ny / 2)
epsr = epsr_min*np.ones((Nx, Ny))
epsr[:, centerPosition-int(wg_width/2):centerPosition+int(wg_width/2)] = epsr_max
#Setup slices
input_slice = Slice(x=np.array(Npml+1), y=np.arange(int(Ny/2-wg_width/2-space_slice), int(Ny/2+wg_width/2+space_slice)))
output_slice = Slice(x=np.array(Nx-Npml-1), y=np.arange(int(Ny/2-wg_width/2-space_slice), int(Ny/2+wg_width/2+space_slice)))
#Get E-Field
#_, _, Ez = simulation.solve(source)
#Find Modeoverlap change across the waveguide
magIn = np.zeros((runSteps,), dtype = 'complex')
magOut = np.zeros((runSteps,), dtype = 'complex')
#magIn_1 = np.zeros((runSteps,))
#magOut_1 = np.zeros((runSteps,))
for i in range(runSteps):
#for i in range(10):
omega=2*np.pi*freqSweep[i] # Angular frequency of the source in 1/s
# Setup source
source = insert_mode(omega, dl, input_slice.x, input_slice.y, epsr, m=1)
# Simulate initial device
simulation, ax = viz_sim(epsr, source, slices=[input_slice, output_slice], i=0, typePlot= 1, flags = [], plotVis = 0)
_, _, Ez = simulation.solve(source)
probesOut = insert_mode(omega, dl, output_slice.x, output_slice.y, epsr, m=1)
probesIn = insert_mode(omega, dl, input_slice.x, input_slice.y, epsr, m=1)
#save complex values
magIn[i] = np.max(probesIn[input_slice.x, input_slice.y])
magOut[i] = np.max(probesOut[output_slice.x, output_slice.y])
#try using mode_overlap again
#magIn_1[i] = mode_overlap(Ez, source)
#magOut_1[i] = mode_overlap(Ez, probesOut)
''' Visualize performance '''
plt.figure()
plt.plot(freqSweep*1e-12, np.abs((magIn)), '--b', lw = 4)
plt.plot(freqSweep*1e-12,np.abs((magIn)), 'rs', ms = 4)
plt.xlim([1, 400]); plt.xticks([1, 100, 200, 300, 400])
plt.ylim([0, 0.4])
plt.grid('on')Lastly, this result led me to another question. When I insert a source along a cross-section, what is Ceviche doing exactly, is it placing a weighted combination of all the possible modes?
No. Ceviche is performing an eigenmode calculation of the cross section and using the field from one eigenmode as the current distribution.
Currently, the cross-section my designed to support the fundamental mode (TM10) of a waveguide at 200THz.
Generally, the fundamental mode of a dielectric waveguide has no cutoff. The mode becomes less and less confined as you go to lower frequencies. You can see this lack of confinement in your Ez field plot. The problem with your simulation is that your source cross section and your probe cross section are not large enough to capture the extent of the waveguide mode. You can increase them, and also the extent of the simulation domain, but as you continue to decrease the frequency you will again hit a point where the mode no longer "fits."
I am not sure what the goal of your study is here. If you are interested in engineering the dispersion of a waveguide, I would suggest focusing only on eigenmode simulations, rather than trying to excite waveguides with sources.
The goal of the study is to observe the change of transmission (power) of a design in a frequency sweep, using the same source (fundamental mode source). I see now, that as I insert a source to the design, a mode is calculated at each iteration, i.e., the excited mode changes, as shown in my previous post.
To set this up properly, I look to use the FDTD tool offered by Ceviche. In this scenario, I can define a Gaussian source based on the same calculated eigenmode from the desired frequency and then look at the spectral power. My problem is how would I do this correctly using Ceviche?
I went ahead and put together a solution based on various examples from your packages, including using the Angler libraries. Could someone point me in the right direction, and share if I am setting this up properly?
Thanks! I appreciate your help!
# -*- coding: utf-8 -*-
"""
In this script, we implement a combination of angler and ceviche to solve a dielectric waveguide design
Following the example of the Forward Mode Grating Coupler
The script should be set in the following manner:
1) Setup the design (here we can define input and output slice as we have had in the past)
2) Setup a Simulation Class Object from Angler to obtain the correct sources and probes to solve the FDTD
3) Transform the problem to FDTD and calculate the coupling efficiency
"""
# Commented out IPython magic to ensure Python compatibility.
import numpy as np
import ceviche
from ceviche import fdfd_ez, fdtd
from ceviche.modes import insert_mode
from ceviche.utils import imarr, aniplot, my_fft
import collections
import matplotlib.pylab as plt
import autograd.numpy as npa
import copy
import sys
sys.path.append('../')
from angler import Simulation, Optimization
from angler.structures import three_port, two_port
from angler.plot import *
# %load_ext autoreload
# %autoreload 2
# %matplotlib inline
""" Plotting Option """
plot_all=1
if plot_all:
print('plotting everything...')
""" Setup the Design (as before) """
centerFreq = 200e12
C = 3e8 #Speed of light
lam = C / centerFreq # Lambda (without considering eps)
omega=2*np.pi*centerFreq # Angular frequency of the source in 1/s
omega0 = omega
dl = (1/30)*lam # Spatial resolution in meters
#dl = 0.02 #Spatial resolition in terms of length
#Nx_l = 10
Nx_l = 10*lam
Nx=int(Nx_l/dl)+1 # Number of pixels in x-direction
Ny=int(Nx_l/dl)+1 # Number of pixels in y-direction
Npml=int(lam/dl)+1 # Number of pixels in the PMLs in each direction
epsr_min=1.0 # Minimum value of the relative permittivity
epsr_max=3.0 # Maximum value of the relative permittivity
space= int(0.25*lam / dl) #Space between the PMLs and the design region (in pixels)
wg_width_l = lam / 2 #6 mm
#wg_width_l = 0.3 #6 mm
wg_width=int(wg_width_l / dl)+1 # Width of the waveguide (in pixels)
space_slice = 32
Slice = collections.namedtuple('Slice', 'x y')
""" Define Parameters """
#Time step setup:
simPeriod = 1 / centerFreq #center frequency period
total_time = 3*simPeriod # total simulation time (s)
band = 0.01e12 #bandwidth of signal
sigma = 1/band
t0 = 0 # delay (s) of pulse center from t=0
#Setup the straight waveguide
#runSteps = 201 #For frequency sweep
#freqSweep = np.linspace(1, 400, runSteps)*1e12
centerPosition = int(Ny / 2)
epsr = epsr_min*np.ones((Nx, Ny))
epsr[:, centerPosition-int(wg_width/2):centerPosition+int(wg_width/2)] = epsr_max
#Add gap
#gap_width = 40
#epsr[centerPosition-int(gap_width/2):centerPosition+int(gap_width/2), :] = 1
#Define additional angler params
lambda0 = C / centerFreq # free space wavelength (m)
NPML = [Npml, Npml]
pol = 'Ez' # polarization (either 'Hz' or 'Ez')
source_amp = 1 # amplitude of modal source (A/L0^2?)
#Setup slices
input_slice = Slice(x=np.array(Npml+1), y=np.arange(int(Ny/2-wg_width/2-space_slice), int(Ny/2+wg_width/2+space_slice)))
output_slice = Slice(x=np.array(Nx-Npml-1), y=np.arange(int(Ny/2-wg_width/2-space_slice), int(Ny/2+wg_width/2+space_slice)))
""" Setup Model Source / Probe """
#Setup the Angler Simulation Object
simulation = Simulation(omega, epsr, dl, NPML, pol, L0= 1)
# compute the grid size the total grid size
print("Computed a domain with {} grids in x and {} grids in y".format(Nx,Ny))
print("The simulation has {} grids per free space wavelength".format(int(lambda0/dl/simulation.L0)))
simulation.plt_eps()
plt.show()
# set the modal source and probes
simulation = Simulation(omega, epsr, dl, NPML, pol, L0= 1)
simulation.add_mode(np.sqrt(epsr_max), 'x', [int(Npml+1), int(Ny/2)], int(Ny/3), scale=source_amp)
simulation.setup_modes()
out = Simulation(omega, epsr, dl, NPML, pol, L0= 1)
out.add_mode(np.sqrt(epsr_max), 'x', [int(Nx-Npml-1), int(Ny/2)], int(Ny/3))
out.setup_modes()
J_out = np.abs(out.src)
#View fdfd simulation
(_, _, Ez) = simulation.solve_fields()
simulation.plt_abs(outline=True, cbar=True);
# get the wg mode profile as an array - change all wg_mode to source (variable created from this line!)
source = np.flipud(np.abs(simulation.src.copy())).reshape((Nx, Ny, 1))
# compute the power in the waveguide mode for normalization
source_p = np.sum(np.square(np.abs(source)))
print('input power of {} in W/L0'.format(simulation.W_in))
# plot the wavegiude mode source array
if plot_all:
plt.imshow(np.real(imarr(source)), cmap='magma')
plt.title('modal source array')
plt.xlabel('x'); plt.ylabel('y')
plt.show()
""" Define the time domain simulation """
# reshape things for the FDTD
eps_base = epsr
eps_total = eps_base
eps_total = eps_total.reshape((Nx, Ny, 1))
source = source.reshape((Nx, Ny, 1))
# make an FDTD and get its time step
F_t = fdtd(eps_total, dl, [Npml, Npml, 0])
dt = F_t.dt
steps = int(total_time / dt)
times = np.arange(steps)
print('-> total of {} time steps'.format(steps))
# make a gaussian source: following Ceviche
gaussian = lambda t: np.exp(-(t - t0 / dt)**2 / 2 / (sigma / dt)**2) * np.cos(omega * t * dt)
source_fn = lambda t: np.abs(source) * gaussian(t)
spect_in = np.square(np.abs(my_fft(gaussian(times))))
delta_f = 1 / steps / dt
freq_x = np.arange(steps) * delta_f
# compute normalization power spectrum
F_norm = fdtd(eps_base.reshape((Nx, Ny, 1)), dl, [Npml, Npml, 0])
measured = []
print('-> measuring spectral power in for base waveguide')
for t_index in range(steps):
if t_index % 1000 == 0:
print(' - done with time step {} of {} ({}%)'.format(t_index, steps, int(t_index / steps * 100)))
fields = F_norm.forward(Jz=source_fn(t_index))
measured.append(npa.sum(fields['Ez'] * np.flipud(source)))
# get spectral power
print('-> computing FFT')
measured_f = my_fft(npa.array(measured))
spect_in_measure = npa.square(npa.abs(measured_f)) / source_p # this is to normalize by the straight waveguide mode power
# plot the source amplitude in the time domain
if plot_all:
plt.plot(times * F_t.dt / 1e-15, gaussian(times))
plt.title('source')
plt.xlabel('time (femtoseconds)')
plt.ylabel('amplitude')
plt.show()
# plot the source power in the frequency domain
if plot_all:
plt.plot(freq_x / 1e12, spect_in, label='direct from source')
plt.plot(freq_x / 1e12, spect_in_measure, label='measured')
plt.xlabel('frequency (THz)')
plt.ylabel('power')
plt.xlim((1, 400))
#plt.xlim((180, 210))
plt.legend()
plt.show()
if plot_all:
if False: # takes an FDTD simulation to generate.
# Make true if you want to see `num_panels` field plots at even intervals
aniplot(F_t, source_fn, steps, component='Ez', num_panels=5)
""" SPECTRAL POWER COMPUTATION """
# reshape other things for FDTD
eps_base = eps_base.reshape((Nx, Ny, 1))
def spectral_power(ff):
""" This function computes the spectral power as a function of fill factor
will autograd/differentiate this with FMD (cevijacobian function)
"""
# setup FDTD using explicit projection into permittivity
eps_total = eps_base
F = fdtd(eps_total, dl, [Npml, Npml, 0])
# compute fields at each time step at the source above
# note: we're solving the reciprocal problem of a waveguide -> free space coupler
measured = []
print('-> running FDTD within objective function')
for t_index in range(steps):
if t_index % 1000 == 0:
print(' - done with time step {} of {} ({}%)'.format(t_index, steps, int(t_index / steps * 100)))
fields = F.forward(Jz=source_fn(t_index))
measured.append(npa.sum(fields['Ez'] * source))
# get spectral power through FFT
print('-> computing FFT')
measured_f = my_fft(npa.array(measured))
spect_power = npa.square(npa.abs(measured_f)) / source_p
return spect_power
# evaluate the function at `ff`
spect = spectral_power(1)
T = spect / spect_in
n_disp = steps // 2 # number of time steps / frequency points to keep
# plot spectral power
if plot_all:
fig, ax1 = plt.subplots()
delta_f = 1 / steps / dt
freq_x = np.arange(n_disp) * delta_f
ax1.plot(freq_x / 1e12, spect_in[:n_disp], label='input')
ax1.plot(freq_x / 1e12, spect[:n_disp], label='measured')
ax1.set_ylabel('spectral power')
ax1.set_xlabel('frequency (THz)')
plt.xlim((1, 400))
#ax1.set_xlim((180, 210))
ax1.legend()
plt.show()
# total powers of the input and measured
P_in = np.sum(spect_in[:steps//4])
P_out = np.sum(spect[:steps//4])
# max power, for normalization
P_in_max = np.max(spect_in[:steps//4])
coupling_efficiency = P_out / P_in
print('calculated a coupling efficiency of {} %'.format(100 * coupling_efficiency))
Hello,
I am a student researcher trying to use your software to design dielectric waveguides. I was hoping someone could please share some insight on the mode overlap function, as I think I may be using it incorrectly. I understand the mode overlap to be the coupling efficiency.
Specifically, I had a concern when simulating a straight waveguide. It is clear that the mode propagates across the waveguide, but the dB10 value of the mode overlap is about -50dB. This value practically stays the same, even as I move the probe (output port) closer to the source. I am using the functions defined in the example notebooks, (e.g., 02_Invdes_intro.ipynb).
The design: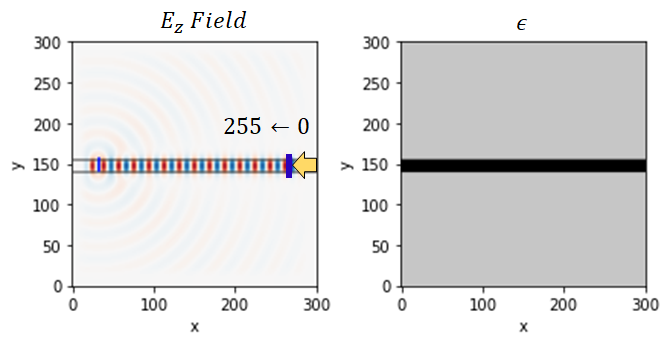
The efficiency as I move the probe closer to the source:
The mode overlap function:
What is wrong?
Thanks, Ricardo Sendrea