QHO Acceptance Rates and ∆Hamiltonian seem wrong

[flipdazed]

Issue

• The accept/reject is fine for SHO but looks too low for QHO
• ∆H is far too high.

Av. acceptance rate : ~87%	Av. acceptance rate : ~58%
Measured av. change in exp{-∆H} ~ 1.3	Measured av. change in exp{-∆H} ~ 95
n_steps=20, step_size=.05, dim = 1; n=1	step_size=.1, n_steps=20, spacing=1., dim = 1; n=10

Resolution

• hmc.dynamics are fine as per checks.
• Check hmc.hmc , hmc.potentials
• Investigate the high variation in the hamiltonian
• Try different configurations of parameters done - still high ∆H
• Measure <x^2> and other measurements to further validate HMC

[flipdazed]

14 - duplicate.

[flipdazed]

The Av. change in hamiltonian not as high as thought. Was not measuring the change - was measuring the absolute value! Edited... main issue post with respect to this.

[flipdazed]

MVG

[flipdazed]

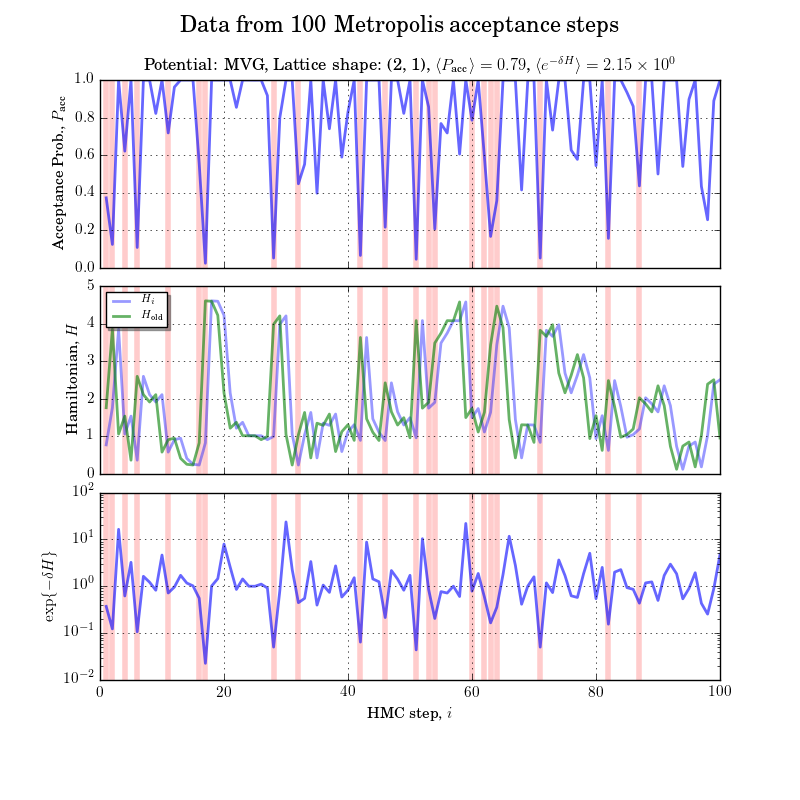
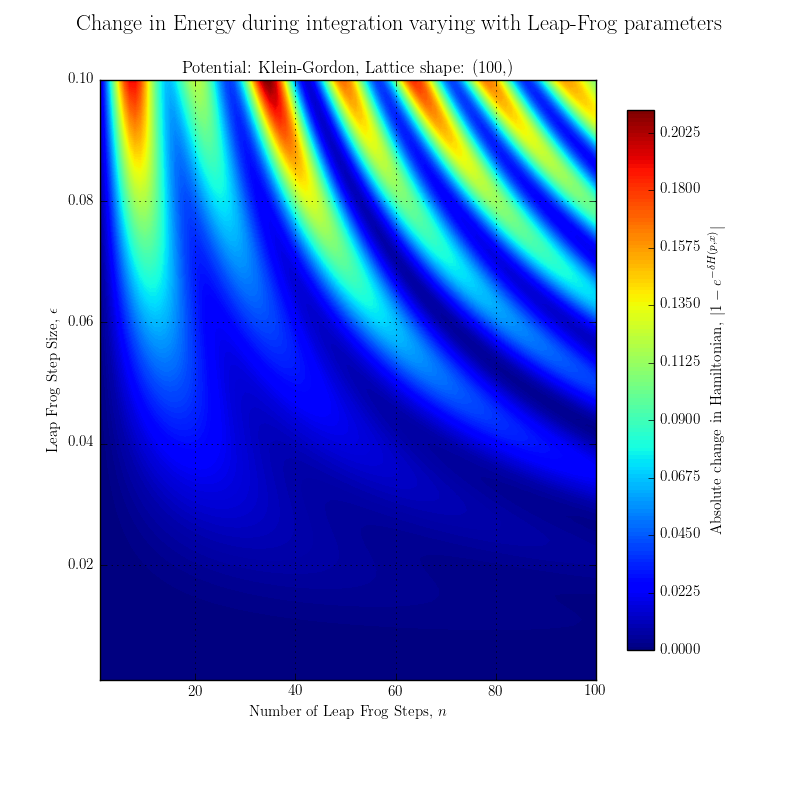
did a full scan of KG potential... (same as QHO with params all set to 1) which looks as if it should be varying as much as indicated above: The values of |1 - exp{-\delta H}| are only varying by ~0.2 !!!

[flipdazed]

ADK This can take a while to reach it equilibrium value $\langle\exp{-\delta H}\rangle = 1$. Ensure that a. You only start measuring after reaching equilibrium. b. Think carefully what value of $\delta H$ to use upon a Metropolis rejection (look at the proof if unsure).

• need to use the h_new from after the metropolis rejection

[flipdazed]

w.r.t. the metropolis acc / res … I excluded the burn-in but I was calculating $\delta H = H{new} - H{old}$ on a rejection, which I suspect should have really been $\delta H = H{old} - H{old}= 0$ as the new configuration was rejected and $H{old} = H{new}$. This is in fact what the sampler does but I was extracting $H{new}$ from within the Metropolis class before it fixed the value for $H{new}$ inside the parent HMC class. I didn’t occur to me to use the assigned value of $H{new}$ rather than the intermediate value of $H{new}$.

[flipdazed]

ADK Remember the proof: $$Z = \int dp\,dq\, e^{-H(q,p)} = \int dp’\,dq’\, e^{-H(q’,p’)}$$ $$=\int dp\,dq\, e^{-H(q’,p’)} = \int dp\,dq\, e^{-\delta H(q,p)} e^{-H(q,p)} = Z\langle e^{\delta H}\rangle$$.

This just makes use of the area-preservation property $dp\,dq = dp’\,dq’$ of symplectic integrators, and has nothing to do with the Metropolis step. Therefore I think what you were calculating was correct.

[flipdazed]

in hmc.move() the original position and momentum, x,p = self.x, self.p were just creating pointers to the memory locations of self.x, self.p and so when their values were updated, they replaced the values of self.x, self.p as well. Hence, the line:

    accept = self.accept.metropolisHastings(h_old=h_old, h_new=h_new)

    # If the proposed state is not accepted (i.e. it is rejected), 
    # the next state is the same as the current state 
    # (and is counted again when estimating the expectation of 
    # some function of state by its average over states of the Markov chain)
    # - Neal, "MCMC using Hamiltnian Dynamics"

    if not accept: p, x = self.p, self.x # return old p,x

was actually implicitly pointless as all new configurations were being accepted by default!

[flipdazed]

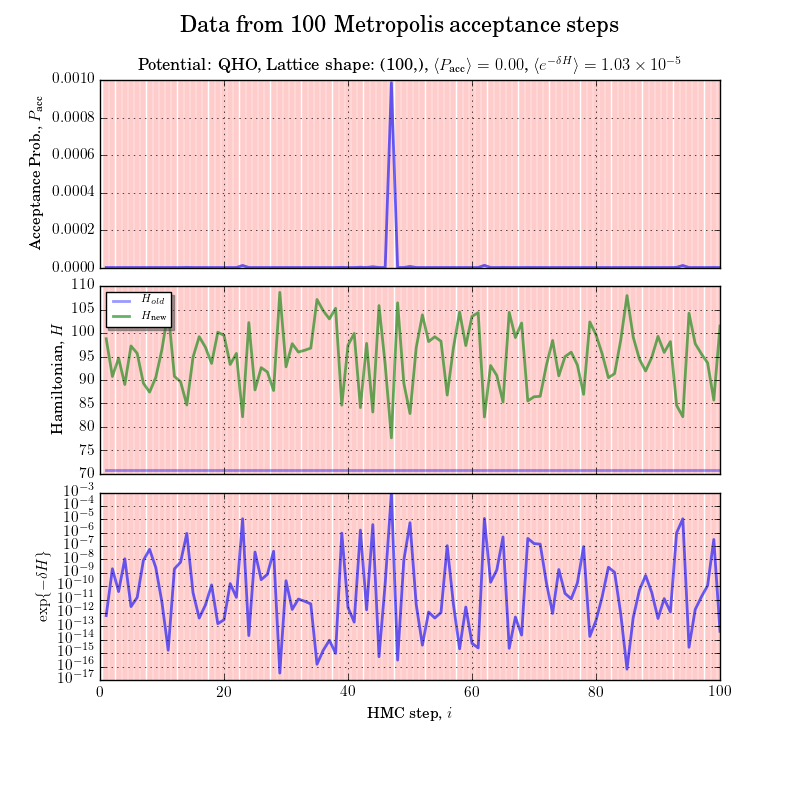
suspect the issue is rooted in python's tendency to share variable memory locations!

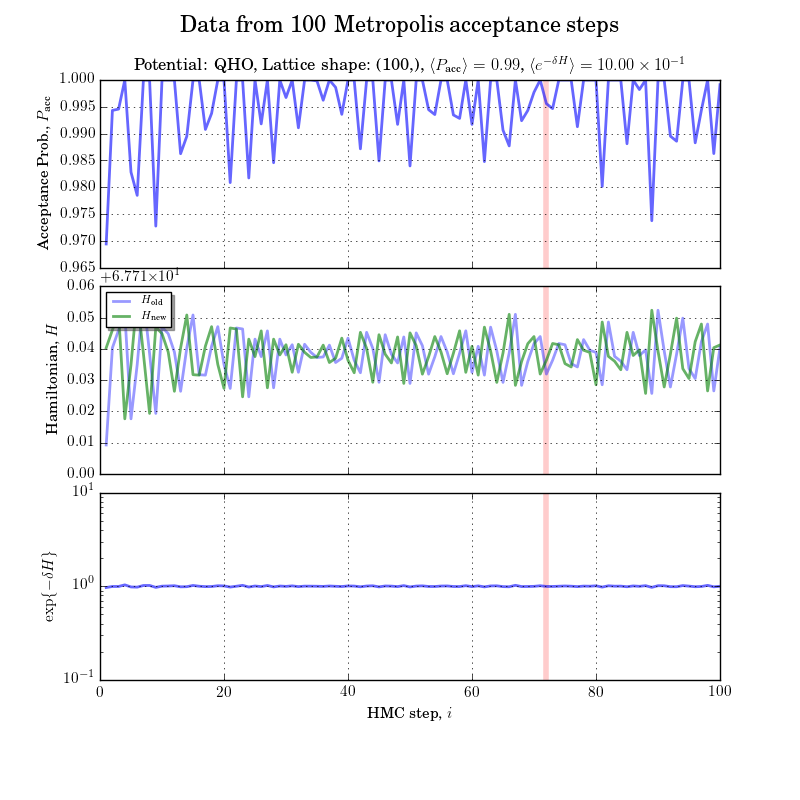
Code changes as follows

• commented out p,x = self.p.copy(), self.x.copy()
• used self.p, self.x in `h_old = self.potential.hamiltonian(self.p, self.x)
• changed self.p -> p and self.x -> x in hmc.dynamics

    def move(self, step_size = None, n_steps = None, mixing_angle=.5*np.pi):
        # Determine current energy state
        # p,x = self.p.copy(), self.x.copy()
        h_old = self.potential.hamiltonian(self.p, self.x)    # get old hamiltonian

        # The use of indices emphasises that the mixing happens point-wise
        p = np.zeros(self.p.shape)
        for idx in np.ndindex(self.p.shape):
            p[idx] = self.momentum.generalisedRefresh(p[idx], mixing_angle=mixing_angle)

        # Molecular Dynamics Monte Carlo
        if (step_size is not None): self.dynamics.step_size = step_size
        if (n_steps is not None): self.dynamics.n_steps = step_size
        p, x = self.dynamics.integrate(self.p, self.x)

        # # GHMC flip if partial refresh
        p = self.momentum.flip(p)

        # Metropolis-Hastings accept / reject condition
        h_new = self.potential.hamiltonian(p, x) # get new hamiltonian
        accept = self.accept.metropolisHastings(h_old=h_old, h_new=h_new)

        if not accept: p, x = self.p, self.x # return old p,x
        return p,x

[flipdazed]

Can see that the see occurs when mixing_angle != 0 i.e. when the momentum is refreshed

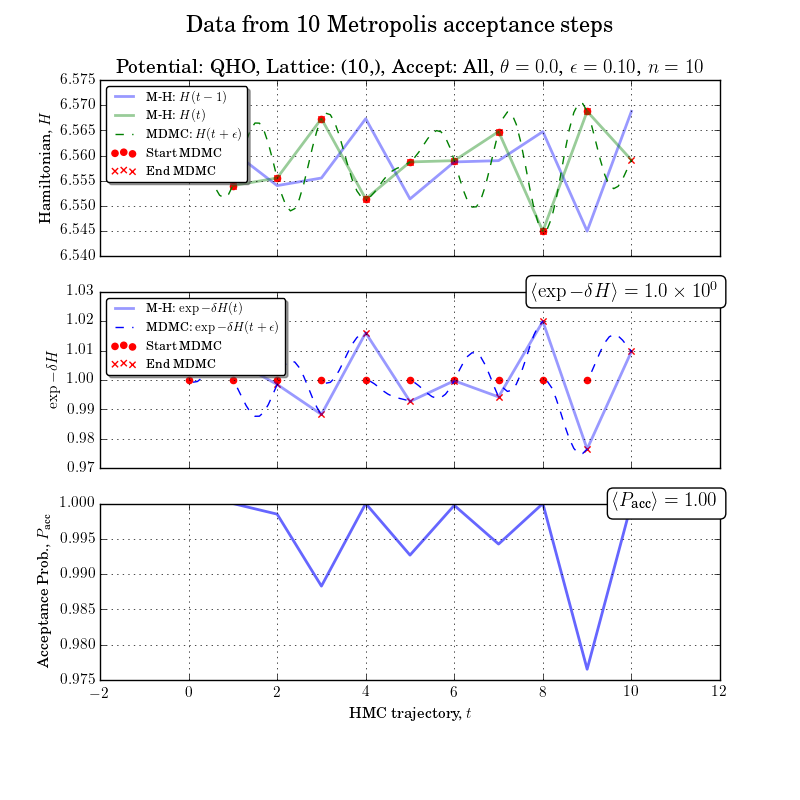
n_samples=10, n_burn_in=0, step_size=0.1, n_steps=10, mixing_angle=0, accept_all = True, spacing=1.

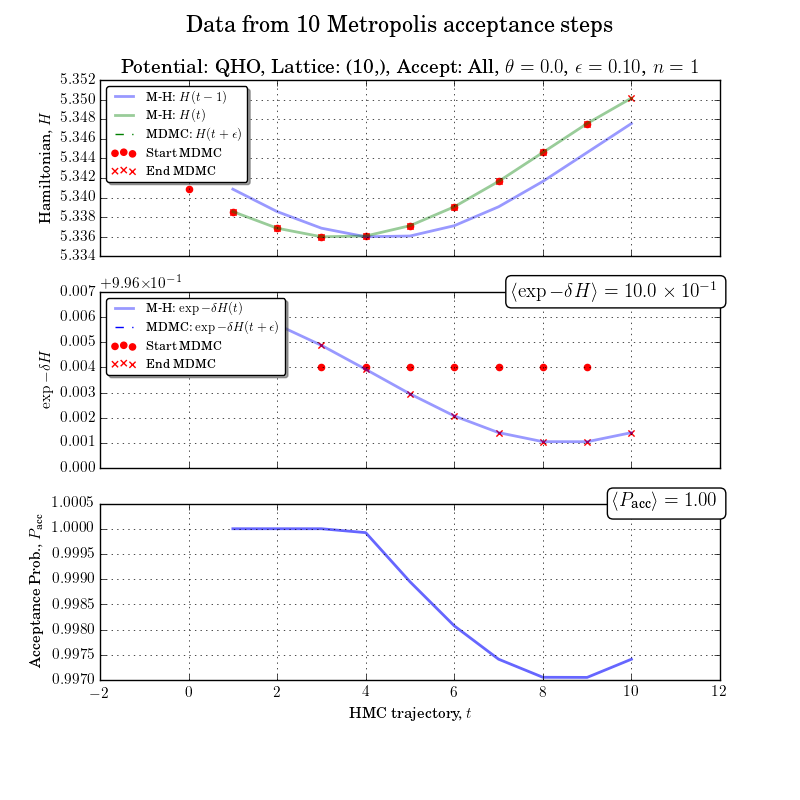
n_samples=10, n_burn_in=0, step_size=0.1, n_steps=1, mixing_angle=0, accept_all = True, spacing=1.

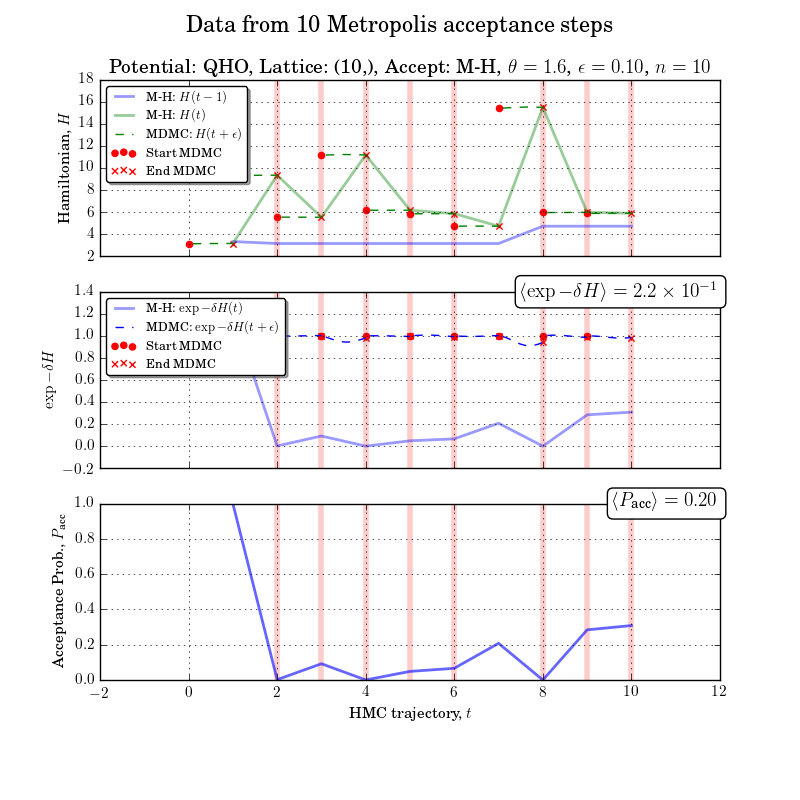
n_samples=10, n_burn_in=0, step_size=0.1, n_steps=10, mixing_angle=np.pi/2., accept_all = False, spacing=1.

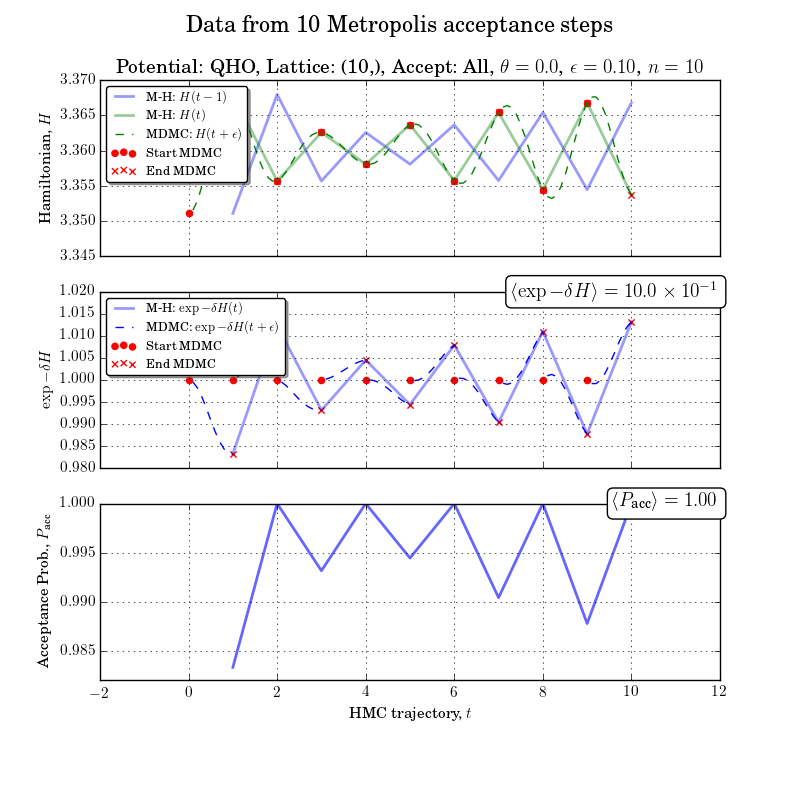
n_samples=10, n_burn_in=0, step_size=0.1, n_steps=10, mixing_angle=np.pi/2., accept_all = True, spacing=1.

[flipdazed]

changing:

    # Determine current energy state
    p0, x0 = p.copy(), x.copy()

    # The use of indices emphasises that the
    # mixing happens point-wise
    for idx in np.ndindex(p.shape):
        # although a flip is added when theta=pi/2
        # it doesn't matter as noise is symmetric
        p[idx] = self.momentum.generalisedRefresh(p[idx], mixing_angle=mixing_angle)

to measuring the initial Hamiltonian after the momentum refreshment seems to be the issue:

    # The use of indices emphasises that the
    # mixing happens point-wise
    for idx in np.ndindex(p.shape):
        # although a flip is added when theta=pi/2
        # it doesn't matter as noise is symmetric
        p[idx] = self.momentum.generalisedRefresh(p[idx], mixing_angle=mixing_angle)

    # Determine current energy state
    p0, x0 = p.copy(), x.copy()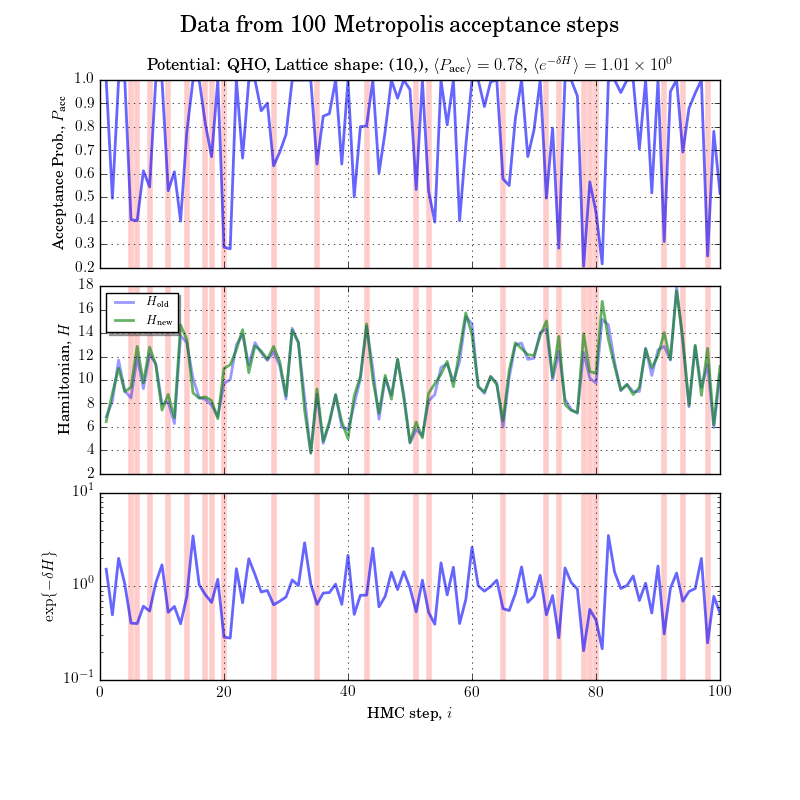

This give a correlation function as:

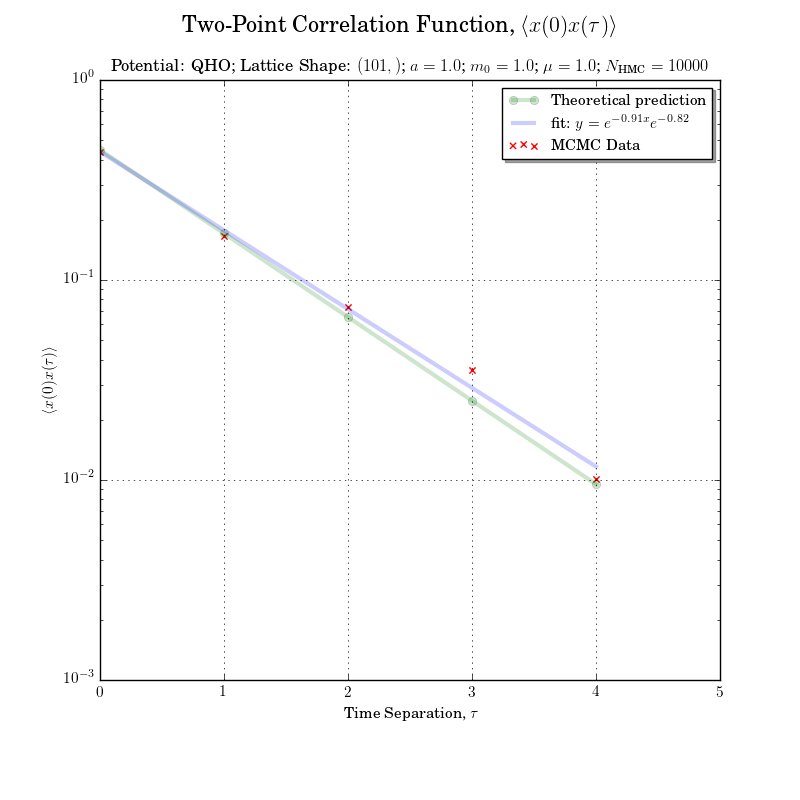
but, still, the number of simulations required is wildly high.

[flipdazed]

nothing more productive to do in this issue - all tests have passed so if there is any further issue it will have to be uncovered by other means.