Thanks a lot for the detailed report, I will investigate the issue and let you know!
Closed reichardtj closed 2 years ago
Thanks a lot for the detailed report, I will investigate the issue and let you know!
Great, thanks a lot. I suppose that means the indexing of the soft constraints is ok, because there appears some conflicting information on that https://github.com/alexliniger/MPCC/issues/49#issuecomment-683686851 - which appears inconsistent with https://github.com/giaf/hpipm/blob/master/doc/guide.pdf where the order for the slacks is input_constraints, state_constraints, polytope constraints, isn't it? In any case, setting the slacks with qp.set('Jsu', np.eye(nu), i) instead of qp.set('idxs', np.array([0, 1]), i) doesn't change the problem.
Also, for what it's worth, one can also make the problem go away by scaling down the running state costs qp.set('Q', Q * 0.01, i) and thinking about it again, we have Q, R, Z all pure L2 and without diagonal entries, the L1 penalties are zero and so in effect, there is hardly any difference in the slacks and the control variables as far as the constraints and cost function is concerned, so maybe there is an additional degree of freedom that the solver exploits. Setting the L1 penalties z to all ones, I get the expected behavior already at qp.set('Q', Q * 0.1, i) but not at the original setting.
Setting the L2 penalties Z to zero and keeping only the L1 penalties at all ones, the expect behavior also shows up with the original setting qp.set('Q', Q, i). Maybe that helps in pinning down the issue.
Sorry for being too concise, I just didn't have the chance yet to look at the problem formulation too, so I didn't intend to say that there are no issues there. And yes, in any case the correct ordering for the slacks is input_bounds first, then state_bounds and finally polytopic_constraints. At the moment I'm independently aware of a performance bug in the implementation of the soft constraints, which may slow convergence down, and I'm slowly finding my way to the root of the issue. I don't know if this is related, but if your issue is not in the formulation of your problem (I will check it as first thing) then I would first get done with my reimplementation work of soft constraints before tracking down your issue, in case it is still there with the new code. My job situation changed recently so now I'm a bit slower here than I used to be :p
I understand and it's not a pressing problem. Looking at the equations again, I noticed that from $Z=\alpha R$ and $J{b,u}=J{s,u}=J$ follows $cost = x^TQx + (u+\alpha sl + \alpha su)^TR(u + \alpha sl + \alpha su)$ and constraints $\underline{u}\leq J(u+sl)$ and $J(u-su) \leq \overbar{u}$. So it seems that there may be a subspace of equivalent solutions after all. I could check this, if if I had access to the slack variables, but the python interface getter doesn't return them as far as I can see. I will try if I can get them and make a corresponding PR. Looking forward to your improvements of the slacked performance anyhow. :-)
Ok I finally managed to find the issue, sorry for taking so long. The issue is that only the diagonal of Zl and Zu should be passed in the solver, and not the entire matrix. The examples in the python folder were wrongly passing the full matrix too: now they are fixed, and I added a basic example using soft constraints.
I think the issue originally comes from the fact that in an older implementation of the python interface, all the different setters were implemented in python, and there the full Zl and Zu were passed and the diagonal of Zl and Zu was extracted in the python interface. Later on, the setters were reimplemented simply calling the newly added C generic setter (which takes as an argument the field name), where for Zl and Zu only a vector containing the diagonal elements is passed. And since the soft constraints were only commented out in that example, they never got fixed.
So sorry for the mistake in the examples, and thanks a lot for the bug reports and the PRs!
BTW I'm still hunting that performance bug, which makes the IPM solver converge linearly if L2 penalty of the slack variables is used, while it correctly converges quadratically if the L1 penalty of the slacks is used. I had an idea about where the issue could be, but at the end everything looks correct there. Still hunting...
brilliant, that works like a charm. Thanks so much! Good Hunting!
Dear @giaf, thank you for the fix
Looks like I have the similar issue in one my project.
The issue is that only the diagonal of Zl and Zu should be passed in the solver, and not the entire matrix.
Is it relevant only for Python interface? If I use C-interface should I use only diagonal for hZl_and hZu in the code below?
d_ocp_qp_set_all(hA_, hB_, hb_, hQ_, hS_, hR_, hq_, hr_,
hidxbx_, hlbx_, hubx_, hidxbu_, hlbu_, hubu_,
hC_, hD_, hlg_, hug_, hZl_, hZu_, hzl_, hzu_,
hidxs_, hlls_, hlus_, &qp);Best Regards, Alex
Hi Alex,
yes this applies to all interfaces, Zl and Zu are expected to be vectors containing the diagonal of the Hessian of the slack variables.
This choice has been made in order to make the processing of the slack variables computationally cheap, with a cost per interior point iteration in the soft constrainted case almost identical to the hard constrainted case.
In case you want to define a non-diagonal Hessian for the soft constraints slack variables, you should implement them e.g. using additional input variables instead.
Dear Gianluca, thanks for maintaining this project!
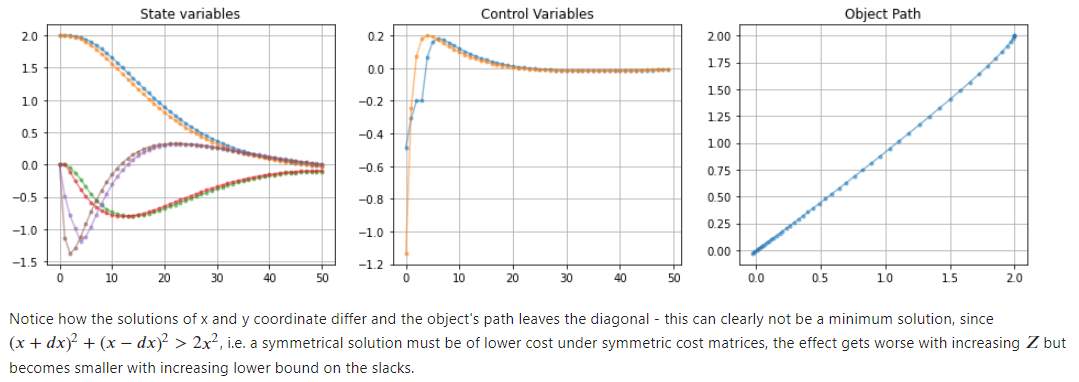
I've been playing around with the ability to soften box constraints on the controls through the introduction of slack variables. However, in a simple 2-D double integrator problem with only quadratic costs, this resulted in a solution in which the x- and y-components of the the solution are not equal. This, however, cannot be due to symmetry in the set-up of the problem - the cost function is invariant under exchange of x and y and so are the initial condition and the terminal state. Both Blasfeo and HPIPM are on the latest version of master compiled using mingw64 on a windows machine with haswell architecture. Interface is Python.
I'm attaching the code to reproduce it and would be more than happy if this could be resolved. I'm a bit uncertain about the indexing of the slack variables, so maybe there is an easy solution - user error. I'm assuming the first $n^b_u$ slack variables correspond to the $n^b_u$ bounds on the controls, the following $n^b_x$ slack variables correspond to the box constraints on $x$ and the remaining $n_g$ slack variables correspond to the polytope constraints.
Thanks a lot for any help!
Best regards Joerg
Here are the images produces the the code below:
without slacks all works as expected: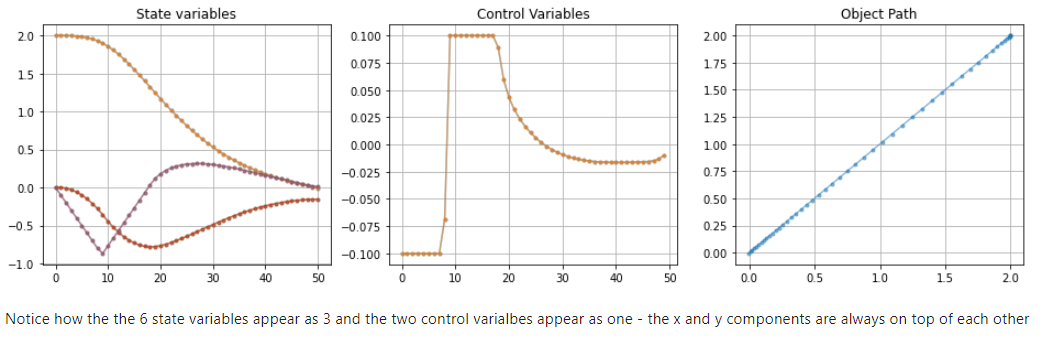
with slacks things look different: