Policy and value heads are from AlphaGo Zero, not Alpha Zero

[gcp]

https://github.com/glinscott/leela-chess/blob/09eb87f76ce85a9a6f9ac697f3abec921e93df0a/training/tf/tfprocess.py#L366

The structure of these heads matches Leela Zero and the AlphaGo Zero paper, not the Alpha Zero paper.

The policy head convolves the last residual output (say 64 x 8 x 8) with a 1 x 1 into a 2 x 8 x 8 outputs, and then converts that with an FC layer into 1924 discrete outputs.

Given that 2 x 8 x 8 only has 128 possible elements that can fire, this seems like a catastrophic loss of information. I think it can actually only represent one from and one to square, so only the best move will be correct (and accuracy will look good, but not loss, and it can't reasonably represent MC probabilities over many moves).

In the AGZ paper they say: "We represent the policy π(a|s) by a 8 × 8 × 73 stack of planes encoding a probability distribution over 4,672 possible moves." Which is quite different.

They also say: "We also tried using a flat distribution over moves for chess and shogi; the final result was almost identical although training was slightly slower."

But note that for the above-mentioned reason it is almost certainly very suboptimal to construct the flat output from only 2 x 8 x 8 inputs. This works fine for Go because moves only have a to-square, but chess also has from-squares. 64 x 8 x 8 may be reasonable, if we forget about underpromotion (we probably can).

The value head has a similar problem: it convolves to a single 8 x 8 output, and then uses an FC layer to transform 64 outputs into...256 outputs. This does not really work either.

The value head isn't precisely described in the AZ paper, and a single 1 x 8 x 8 is probably good enough, but the 256 in the FC layer make no sense then. The problems the value layer has right now might have a lot to do with the fact that the input to the policy head is broken, so the residual stack must try to compensate this.

[jkiliani]

What's the Elo rating for Gnuchess at the settings you used?

[kiudee]

@Error323 Good job. I am going to try playing that network. I am also currently running training on the Stockfish data with a 10x128 network: It’s using the following parameters:

• Value loss weight 0.02
• Policy head: 64x8x8
• Value head: 32x8x8 -> 256

For now (at iteration 220k) it still plays quite bad, but through search it is typically able to improve its moves, which suggests that the learned value head is providing some benefit.

[glinscott]

@Error323 congrats! That's awesome progress :). One thing I'm curious about - which version of GnuChess did you use?

Here are the ratings for the different versions from CCRL: http://www.computerchess.org.uk/ccrl/4040/cgi/compare_engines.cgi?family=GNU%20Chess&print=Rating+list&print=Results+table&print=LOS+table&print=Ponder+hit+table&print=Eval+difference+table&print=Comopp+gamenum+table&print=Overlap+table&print=Score+with+common+opponents

[Error323]

It's 6.2.2 the default in Ubuntu 16.04. I don't know the ELO rating. Note that I handicapped it severely with 30 moves per minute.

[Error323]

@glinscott that site is a goldmine for supervised learning :heart_eyes: The PGN files seem to be available.

[kiudee]

I am aborting my training run now. This is the state after 400k steps:

Even though it has an accuracy of almost 80% on the stockfish data, it still has problems finding good moves with a low number of playouts. I suspect there might be a problem of variety in the Stockfish data, causing it to have similar positions in train/test. The learned value function is able to compare positions relatively (which is why it improves its move choice when letting it do more playouts), but the absolute score is always hovering around 55% for white. It looks like a local optimum where it learned to adjust the score slightly based on the position.

If you want I can upload weights and config, but the file is too large for attaching it here.

[Error323]

Even though it has an accuracy of almost 80% on the stockfish data, it still has problems finding good moves with a low number of playouts. I suspect there might be a problem of variety in the Stockfish data, causing it to have similar positions in train/test.

I agree. I think that even though the final gamestates may be different, the first n ply share many similarities. Given your graphs it should be annihilating everything, but the data compared to the entire chess gametree is too sparse.

[kiudee]

Just to get an idea, this is the PV of the start position including the points where it changed its mind:

Playouts: 1412, Win: 55.40%, PV: g1h3 h7h6 e2e4 e7e6 c2c3 g7g6 f1b5
Playouts: 2908, Win: 55.41%, PV: g1h3 h7h6 e2e4 b8c6 f1a6 g7g6 d1f3 g8f6
Playouts: 4405, Win: 55.35%, PV: g1h3 h7h6 e2e4 e7e5 c2c3 c7c6 f1a6
Playouts: 5912, Win: 55.29%, PV: g1h3 h7h6 e2e4 e7e5 c2c3 f7f6 f1c4
Playouts: 11568, Win: 55.25%, PV: g1h3 h7h6 e2e4 d7d5 f1b5 b8c6 d1f3 g7g6 d2d3 g8f6
Playouts: 37993, Win: 55.64%, PV: e2e4 b8c6 g1h3 h7h6 f1a6 g7g6
Playouts: 110811, Win: 56.01%, PV: e2e4 d7d5 e4e5 d5d4 g1h3 d4d3 f1e2 h7h6 c2c3 c8d7 e2f3
Playouts: 498938, Win: 56.21%, PV: e2e4 e7e5 g1f3 f8c5 d2d4 c5d4 c1g5 h7h6 h2h4 d4e3 d1d4 e3c1 g2g3 c1e3 d4e3 g7g6 e3d3
eval=0.562360, 500001 visits, 15851401 nodes, 500001 playouts, 563 n/s
bestmove e2e4

[kiudee]

I found something interesting. I gave the network trained by @Error323 the following position from the 10th game of AlphaZero vs Stockfish:

rnb2r2/p3bpkp/1ppq3N/6p1/Q7/2P3P1/P4PBP/R1B2RK1 w - - 0 19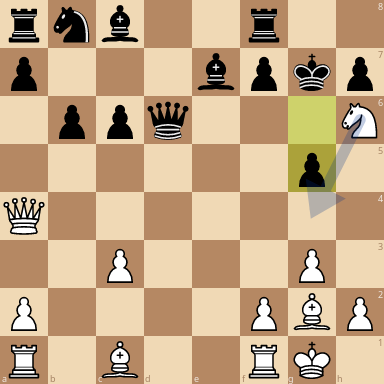

After 325950 playouts the network prefers the move Re1:

...
Playouts: 324241, Win: 56.87%, PV: h6f7 f8f7 c1e3 e7f6 a1d1 d6e7 e3d4 b6b5 a4c2 f6d4 c3d4 c8g4 d4d5 e7f6 h2h3 g4f3 g2f3 f6f3 f1e1 c6d5 d1d3 f3f5 c2d2 d5d4 d3d4 b8c6 d4d5 f5f6 d2g5 f6g5 d5g5 g7f8 e1e4 a7a6 g5c5 a8c8 g1g2 f7f6 f2f4
Playouts: 325950, Win: 56.85%, PV: f1e1 c8e6 c1e3 g7h6 h2h4 b8d7 a1d1 d7c5 h4g5 h6g6 a4h4 d6d1 e1d1 h7h5 g2e4 g6g7 e4f3 f8h8 h4d4 g7g6 d4e5 h8h7
...
Playouts: 864489, Win: 58.53%, PV: f1e1 c8e6 c1e3 g7h6 h2h4 b8d7 a1d1 d7c5 h4g5 h6g7 a4h4 d6d1 e1d1 f8d8 e3d4 g7g8 h4h6 e7f8 h6f6 d8d4 d1d4 a8c8 d4d8 c5d7 f6e6 c8d8 e6c6 d7e5 c6c7 d8d1 g2f1 e5f3 g1g2 f3g5 c7a7 f8c5 f1e2 d1d2 a7a8 g8g7 g2f1 d2a2 f2f4

[Error323]

@kiudee it's not immediately obvious to me. Could you elaborate?

[kiudee]

If you analyze the position with Stockfish, it thinks the move is losing/even (depending on depth). Yet, in the game it is soon apparent that white is winning. Your network also seems to prefer this move after some time. This does not mean that the network has the same deep understanding of the position that AlphaZero has, but it is intriguing.

Stockfish at depth 42:

42 [-0.54]  19.... Kxh6 20.h4 f6 21.Rxe7 Qxe7 22.Ba3 c5 23.Bxa8 Kg7 24.hxg5 fxg5 25.Bg2 Bf5 26.c4 Kh6 27.Rd1 Bg4 28.Rf1 Qd7 29.Qc2 Nc6 30.Bxc6 Qxc6 31.f4 gxf4 32.Bc1 Qe6 33.Rxf4 Rxf4 34.Bxf4+ Kg7 35.Kf2 Qf6 36.a3 Be6 37.Qe4 Qb2+ 38.Kg1 Qa1+ 39.Kh2 Qa2+ 40.Kg1 Qxc4 41.Qxc4 Bxc4 42.Bb8 a6 43.Ba7 b5 44.Bxc5 a5 45.Bd4+ Kg6 46.Kf2  (1176.08)

[lp--]

Puzzling it does not consider taking knight at all

Detecting residual layers...Loading kbb-net/kbb1-64x6-796000.txt
v1...64 channels...6 blocks.
position fen r2qk2r/p2nppb1/2pp1np1/1p2P1Bp/3P2bP/2N2N2/PPPQ1PP1/2KR1B1R w kq - 1 10
go
Playouts: 304, Win: 58.96%, PV: f1e2 d6e5 d4e5 f6h7 g5f4 d8a5 c1b1 d7c5 f3d4
...
Playouts: 898, Win: 60.12%, PV: d1e1 d6e5 d4e5 f6h7 g5h6 g7h6 d2h6 g4f3 g2f3 d8a5 h6g7
...
Playouts: 3337, Win: 59.96%, PV: d4d5 d7e5 f3e5 d6e5 f2f3 g4d7 d5c6 d7c6 f1b5 c6b5 c3b5 d8d2 d1d2 e8g8 h1e1 f8c8

[lp--]

Here it decides for no reason to give up knight.

Detecting residual layers...Loading kbb-net/kbb1-64x6-796000.txt
v1...64 channels...6 blocks.
position fen r2qk1nr/p2nppb1/2pp2p1/1p2P1Bp/3P2bP/2N2N2/PPPQ1PP1/2KR1B1R b kq - 0 9
go
Playouts: 304, Win: 39.18%, PV: d6e5 d4d5 g4f3 g2f3 b5b4 c3e4 d8b6 d5d6 g8f6
...
Playouts: 2157, Win: 37.97%, PV: g8f6 f1e2 b5b4 e5f6 b4c3 d2c3 d7f6 c3c6 g4d7 c6c4 a8c8 c4b3 e8g8

But stockfish thinks that black is even better with d6e5 info depth 20 seldepth 32 multipv 1 score cp 52 nodes 2709905 nps 1259249 hashfull 872 tbhits 0 time 2152 pv d6e5 d4e5 d7e5 f3e5 d8d2 d1d2 g7e5 f1d3 g8f6 h1e1 f6d7 f2f4 e5f6 g2g3 a7a6 c3e4 f6g5 e4g5 d7f6 d3e4 f6e4 g5e4 e8f8 e4c5 a8a7 d2d8 f8g7 d8h8 g7h8 e1e3 h8g7

[lp--]

Positions are from the full game it played with 1600 playouts

1. e4 g6 2. d4 Bg7 3. Nc3 d6 4. h4 h5 5. Bg5 c6 6. Qd2 b5 7. Nf3 Bg4 8.
O-O-O Nd7 9. e5 Ngf6 10. d5 Nxe5 11. Nxe5 dxe5 12. dxc6 Qa5 13. f3 Be6 14.
Nxb5 Qb6 15. Bc4 Qxc6 16. Bxe6 fxe6 17. Rhe1 Qxb5 18. Qd3 Qxd3 19. Rxd3 Kf7
20. Rxe5 Rhc8 21. Rde3 Rc6 22. c3 Rb8 23. Ra5 a6 24. Bxf6 Bxf6 25. Kc2 Bxh4
26. Re4 Bf6 27. Rf4 h4 28. Raa4 g5 29. Rfb4 Rd8 30. Re4 Rd5 31. Re2 a5 32.
Rd2 Rcc5 33. Re2 Rc6 34. Rd2 Re5 35. Rdd4 Rd6 36. Re4 Red5 37. Re2 Be5 38.
Rae4 Bf4 39. a4 e5 40. b4 Kf6 41. Kb3 Kf5 42. Kc4 g4 43. fxg4+ Kxg4 44.
bxa5 Rxa5 45. Kb4 Ra8 46. Rxe5 Bxe5 47. Rxe5 Kg3 48. Rg5+ Kf4 49. Rg7 e5
50. a5 e4 51. Kc5 Rd2 52. Kb6 Rb2+ 53. Kc6 Rxa5 54. c4 e3 55. c5 Rc2 56.
Kd6 Raxc5 57. Re7 Rg5 58. Rh7 e2 59. Rxh4+ Kg3 60. Re4 Kxg2 61. Re3 Kf2 62.
Re8 Rd2+ 63. Kc7 Rc2+ 64. Kd6 Rd2+ 65. Kc7 Rd4 66. Rf8+ Ke3 67. Re8+ Kf2
68. Rf8+ Ke3 69. Re8+ Kd2 70. Rd8 Rxd8 71. Kxd8 e1=Q 72. Kd7 Rg7+ 73. Kd6
Qd1 74. Ke5 Qf3 75. Kd4 Qf4+ 
Score: 0

[amj]

@Error323 Scanning through this, the periodicity in the earlier graphs is almost certainly an artifact of the shuffling behavior. We were rather constantly surprised by the shuffle behavior not quite doing what we expected. We ended up turning the shuffle size up to almost the total number of steps we take per generation (2M)... not quite the same as what you're doing w/ SL here but that periodicity really, really jumped out at me.

[amj]

@Error323 re: how to see when to drop the learning rate. It was suggested to us that we monitor the gradient updates as a way to see when it's time to drop the rate, and adjust accordingly.

[Error323]

We were rather constantly surprised by the shuffle behavior not quite doing what we expected. We ended up turning the shuffle size up to almost the total number of steps we take per generation (2M)...

Well this is somewhat scary. When using a shuffle buffer of 2^18 my memory consumption already went through the roof.

how to see when to drop the learning rate. It was suggested to us that we monitor the gradient updates as a way to see when it's time to drop the rate, and adjust accordingly.

Thanks! This is very different from what I had in mind, and probably better! I'm gonna examine code and comments!

[gcp]

Well this is somewhat scary. When using a shuffle buffer of 2^18 my memory consumption already went through the roof.

In Leela Zero this was solved by dropping 15/16th of the training data randomly. This trades of 16x the input processing CPU usage for a 16 times saving of memory. You can make this bigger if you have more or faster cores in the training machine.

Whether this is usable somewhat depends on the input pipeline.

But yes, shuffle buffer by themselves aren't good enough if the training data is sequential positions from games.

[amj]

we dropped data as well, sampling only 5% of the positions (here). This is for RL though not SL -- i haven't done much with SL

[glinscott]

Fixed now :).

[gcp]

The value head has a similar problem: it convolves to a single 8 x 8 output, and then uses an FC layer to transform 64 outputs into...256 outputs. This does not really work either. The value head isn't precisely described in the AZ paper, and a single 1 x 8 x 8 is probably good enough, but the 256 in the FC layer make no sense then.

Turns out that is actually what they did. From empirical experiments, doing the 1x1 256->1 down-convolution before the FC layers works very well (and better than doing, say, 1x1 or 3x3 256->32 and using that as FC input). That said, making the value head FC layer bigger(!) than the input to it still seems strange to me and looks like it was carried over from the other games more than anything else.