On the Coffee Lake block diagram, I see 2 FP FMA units:
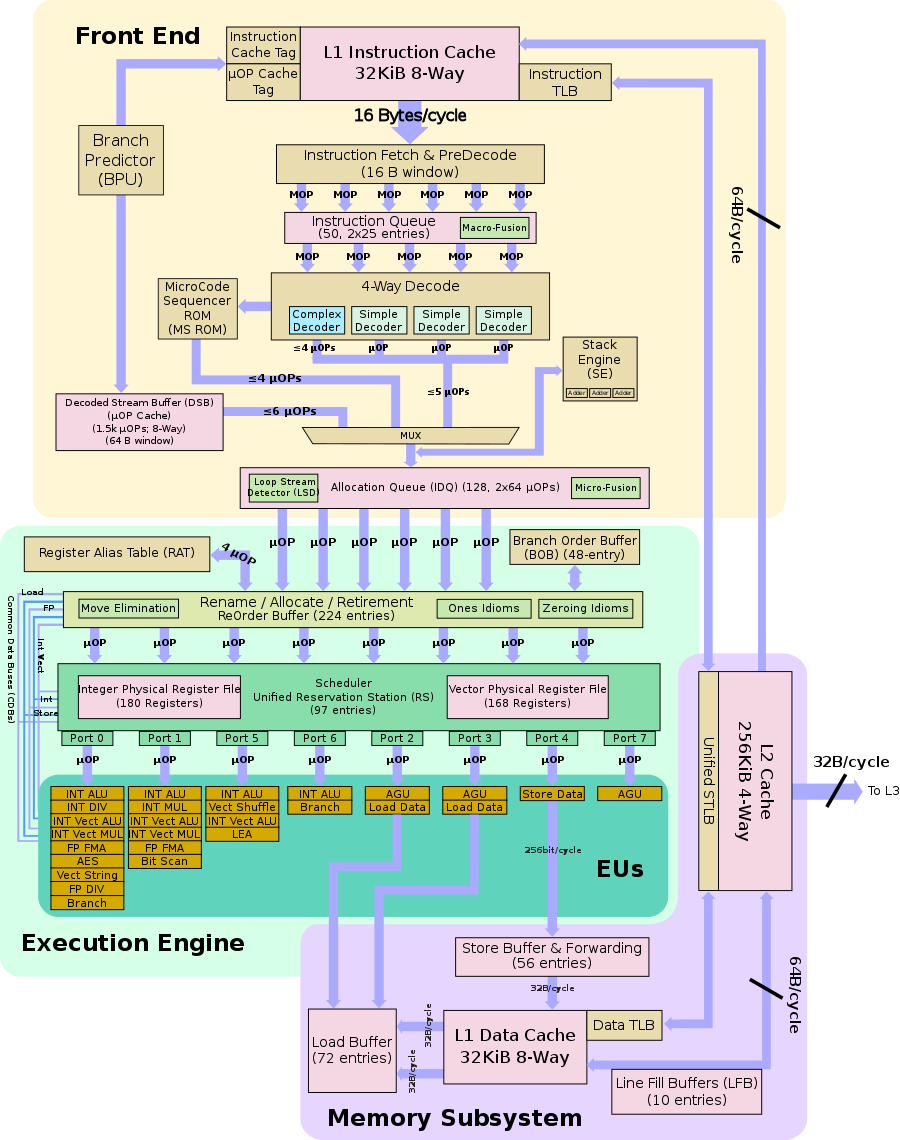
Rerunning the math, but with 2 FP FMA's doubles the number of flops, yielding 576 GFlops, which is above what Halide reported. Halide achieves 93.3% of theoretical peak, with these calculations, at 3GHz.
When testing performance_matrix_multiplication, the actual peak flops is much higher than the theoretical peak flops. I work on Intel Core i5-8500B. Coffee Lake architecture, has one 256-bit FMA (Fused Multiply-Add) unit, which can execute 8 single-precision floating-point operations each time, The theoretical peak value should be
6 cores × 3.0 GHz × 8 FLOPs/cycle * 2 (mul + add) = 288 GFlops.However, the actual peak value of the calculation in the output I got isHalide: 3.631948ms, 537.558090 GFLOP/s, which is even higher than the theoretical peak flops after turbo (4.1 GHz). I'd like to know where the possible problem lies. Thanks for any possible answers.