L2-norm for diagonal paths

[daniel1896]

Suggestion: Please add the option to use the L2-norm (euclidean distance) for diagonal paths. It does not matter in those maze examples. But for more open environments, as shown in the example below, the path is not optimal on the L2-norm.

[daniel1896]

I fixed it by replacing the infinity norm with

// L_2 norm
inline float l2_norm(int i0, int j0, int i1, int j1) {
  return sqrt(pow(i0 - i1, 2) + pow(j0 - j1, 2) * 1.0);;
}

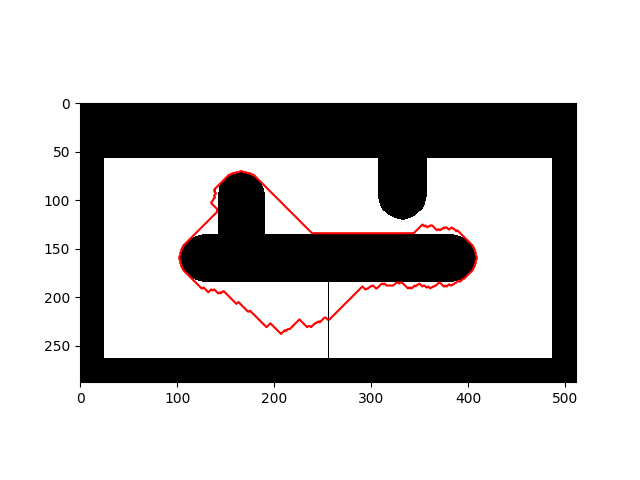
I am not sure if the * 1.0 is really needed, as I am not very familiar with C++. I got it from here: https://www.geeksforgeeks.org/program-calculate-distance-two-points/ You might want to add that as an option and not replace it like I did. Here is the result I got with this change:

[hjweide]

This implementation follows the definition that the shortest path on the grid is the set of vertices (i, j) such that the sum of the values associated with the vertices in the set is minimized. The reason for this is that it was written for the purpose of extracting contours from images rather than uniform grids.

By replacing the L_{\inf} norm with the L_2 norm you are not changing the cost of the shortest path, but only the heuristic estimate of the path. You'll still get the optimal path (it's still an admissible heuristic), but you'll pay for it in terms of efficiency because the L_2 norm doesn't eliminate high-cost paths as well. Taken to the extreme, you could use the trivial heuristic of 0 and arrive back at Dijkstra's algorithm.

If you're only interested in uniform grids and prefer paths that resemble L_2 optimal paths, the simplest thing to do may be to break ties by adding non-diagonal neighbors to the priority queue before the diagonal neighbors (I haven't checked this – caveat emptor.)

But of course, if you're only interested in shortest paths on uniform grids, you should be using jump point search instead of A* :)

[daniel1896]

Thank you for your suggestion, I will take a look at jump point search.