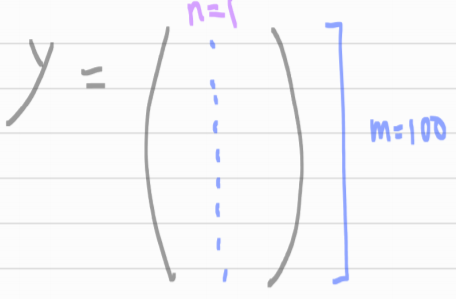
만약 x, y가 위처럼 한개로 정해진 것이 아니라 matrix 형태처럼 복잡하다면?

해결법 : Normal Equation (정규 방정식)


X_b = np.c_[np.ones((100, 1)), X] # 모든 샘플에 x0 = 1을 추가합니다.
X_b
- 1인 칼럼을 추가함으로써, bias(theta_0)를 구할 수 있음

theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
theta_best
- [theta_0, theta_1] 차례대로
Transpose, Inverse, dot product

 이거 왜 x가 0일 때 y가 4여서 theta_0이 4여야 best parameter인지 이해안가!
이거 왜 x가 0일 때 y가 4여서 theta_0이 4여야 best parameter인지 이해안가!






















정규 방정식을 이용한 선형 회귀
np.random.rand(100, 1)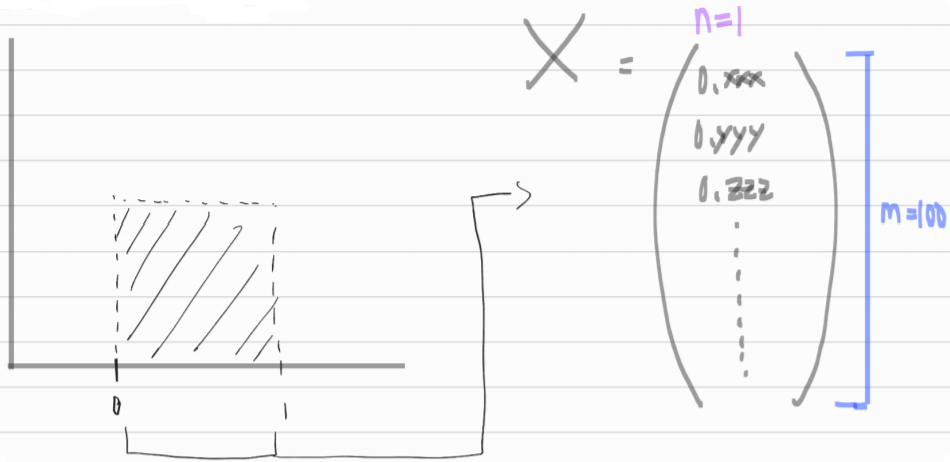
np.random.randn(100, 1)