Sensor noise and external disturbances may cause unstable or undesired responses in the system. To combat this, we have chosen to implement a second order Butterworth filter -- a type of low pass filter. The benefit of a second order Butterworth filter compared to a first order RC low pass filter by increasing attenuation and reducing the transition band.
By using the second order filter, we marginally increase the complexity while notably improving desired behavior. Our goal is to implement this in discrete time to better read the sensor values from the sonar, pH (#6), and EC (#5) sensors. To design ours for the Raspberry Pi, we loosely followed the procedure from Curio Res' tutorial.
To design the desired filter, we must first choose a cutoff frequency to create the filter transfer function and its coefficients.
where s_k is the k-th pole of the transfer function.
We first assume DC gain G = 1 and normalize cutoff frequency (w_c = 1) which will then be modified to fit the chosen cutoff frequency. This allows us to easily calculate the Butterworth characteristic equation as a sum.
import numpy as np
from scipy import signal
a = np.zeros(self.n + 1)
gamma = np.pi / (2.0 * self.n)
a[0] = 1 # first coeff always 1
for k in range(self.n):
rfac = np.cos(k * gamma) / np.sin((k+1) * gamma)
a[k+1] = rfac*a[k]
# Adjust for cutoff frequency
self.b = np.zeros(self.n + 1)
for k in range(self.n + 1):
self.b[self.n - k] = a[k] / pow(self.wc, k)
# coefficients stored in b
We can then use scipy to discretize these coefficients:
The number of coefficients should come out to be n+1 or one greater than the order of the filter. We then turn that into an equation we can use to compute the new filtered value.
Nb = len(self.num)
# check if we have prior values to pass into filter
try:
self.f_vals
except NameError:
self.f_vals = np.zeros(self.n)
self.s_vals = np.zeros(self.n)
# use coeffs and prior discrete values to get new filtered value
filt_new = self.num[0]*s_val
for f, y, a, b in zip(reversed(self.f_vals), reversed(self.s_vals), self.den[1:], self.num[1:]):
filt_new += a*f + b*y
We can then store the new filtered value and sensor values for subsequent uses.
Sensor noise and external disturbances may cause unstable or undesired responses in the system. To combat this, we have chosen to implement a second order Butterworth filter -- a type of low pass filter. The benefit of a second order Butterworth filter compared to a first order RC low pass filter by increasing attenuation and reducing the transition band.
By using the second order filter, we marginally increase the complexity while notably improving desired behavior. Our goal is to implement this in discrete time to better read the sensor values from the sonar, pH (#6), and EC (#5) sensors. To design ours for the Raspberry Pi, we loosely followed the procedure from Curio Res' tutorial.
To design the desired filter, we must first choose a cutoff frequency to create the filter transfer function and its coefficients.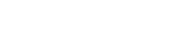
where s_k is the k-th pole of the transfer function.
We first assume DC gain G = 1 and normalize cutoff frequency (w_c = 1) which will then be modified to fit the chosen cutoff frequency. This allows us to easily calculate the Butterworth characteristic equation as a sum.
We can then modify the normalized polynomial with our chosen cutoff frequency.
![image] (https://user-images.githubusercontent.com/17360719/154150570-40cc8f0f-c9a9-4934-b67f-3b260c3d00d0.png)
We can then use scipy to discretize these coefficients:
The number of coefficients should come out to be n+1 or one greater than the order of the filter. We then turn that into an equation we can use to compute the new filtered value.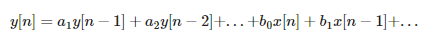
We can then store the new filtered value and sensor values for subsequent uses.