JS.Benchmark issues

[jdalton]

I will try to fill in the gaps when I have some spare time but I figured I would give you a heads up.

Here is a quick list of problems:

1. Your formula for margin of error and standard deviation are incorrect
2. You don't account for poor timer resolution in IE < 9
3. You rely on a user passed run count which ties into #2
4. Your setup methods are called in batch before the test run so things like adding dom elements the benchmark would remove won't work as well.

[mathiasbynens]

Disclaimer: John-David developed Benchmark.js which is used on jsPerf and wrote about bulletproof JavaScript benchmarks before. He’s seen all kinds of timer issues :)

[jcoglan]

Caveat: I wrote this primarily to have a portable benchmark lib for server-side code, for browser stuff I would go with jsPerf.

Re: 1. Could you explain how my error calculation is wrong?

Re: 4. This is by design, so that all the tests can be run in one block and timed that way. Trying to time single-run tests between setup periods is really inaccurate, and like I say I don't use it for DOM stuff. I mostly use the setuo method to create some data structure before testing an operation on it, where I don't want the setup time of the data to factor into the test.

[jdalton]

Caveat: I wrote this primarily to have a portable benchmark lib for server-side code, for browser stuff I would go with jsPerf.

Benchmark.js actually runs on Narwhal, Node.js, RingoJS, and Rhino environments as well as lots of old and new browsers. Interestingly we both started benchmark projects around the same time. I started contributing to Benchmark.js on Oct 6th 2010 and you started JS.Benchmark on Oct 11th.

The timer resolution concern of item 2 actually applies to all environments to some extent. The uncertainty of a measurement is generally half the smallest measurable value. In JavaScript the smallest measurable value is usually 1ms so the uncertainty is 0.5ms. To get a percent uncertainty of 1% you would have to run a test for at least 50ms (1 / 2 / 0.01 = 50).

You can remove the option to specify a run count, item 3, and instead calculate how many runs are needed to get a percent uncertainty at-or-below 1%. Benchmark.js does this by performing a couple test runs and calculating how many runs are needed to meet or exceed the minimum time.

Here is a comparison of the Node.js results generated by JS.Benchmark and Benchmark.js using tests from your recent blog post:

JS.Benchmark:

 BENCHMARK [63ms +/- 21%] prototype
 BENCHMARK [290ms +/- 9%] constructor

Benchmark.js:

prototype x 28,843,917 ops/sec ±1.23% (44 runs sampled)
constructor x 3,931,885 ops/sec ±2.76% (45 runs sampled)

When I take the data from Benchmark.js and calculate how long it would take to run 1,000,000 times to match the test execution count of JS.Benchmark I get roughly

35ms for test "prototype"
254ms for test "constructor"

The reported times for both tests are consistently less from run to re-run with Benchmark.js.

[jdalton]

Re: 1. Could you explain how my error calculation is wrong?

Mean

Just to ease into the formulas here is a quick review of the formula/notation for the population and sample mean. I have linked to additional Khan Academy videos in each section. I recommend watching them as they cover more info than this reply.

Here is the formula for the population mean:

Here is the formula for the sample mean (a.k.a. the estimate of the population mean):

In this case the formulas for population and sample means are identical except for notation.

var mean = sample.reduce(function(sum, x) {
  return sum + x;
}) / sample.length;

Variance

Your formula for variance is incorrect. You are using the formula for the population variance instead of the sample variance. When benchmarking you are taking samples from an unknown population. The standard deviation is the square root of the variance.

Here is the formula for the population variance:

var populationVariance = sample.reduce(function(sum, x) {
  return sum + Math.pow(x - mean, 2);
}, 0) / sample.length;

Here is the formula for the sample variance (a.k.a the estimate of the population variance):

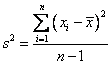
var sampleVariance = sample.reduce(function(sum, x) {
  return sum + Math.pow(x - mean, 2);
}, 0) / sample.length - 1;

The difference between formulas is that the formula for sample variance has you divide by the sample size minus 1.

Standard Deviation

You are confusing the sample standard deviation (a.k.a the estimate of the population standard deviation) with the standard error of the mean (a.k.a the standard deviation of the sampling distribution of the sample mean).

Here is the formula for the sample standard deviation:

var sampleDeviation = Math.sqrt(sampleVariance);

Standard Error of the Mean

Here is the formula for the standard error of the sample mean which is used to resolve the margin of error:

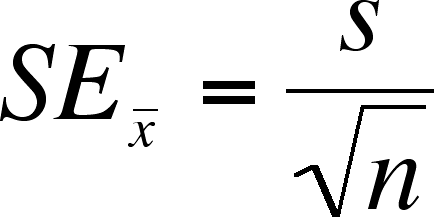
var standardError = sampleDeviation / Math.sqrt(sample.length);

Margin of Error

Because you collect such a small sample size the sampling distribution isn't a normal distribution but rather a t-distribution.

Here is the formula for the margin of error at 95% confidence:

/**
 * T-Distribution two-tailed critical values for 95% confidence
 * http://www.itl.nist.gov/div898/handbook/eda/section3/eda3672.htm
 */
var distribution = {
  '1':  12.706,'2':  4.303, '3':  3.182, '4':  2.776, '5':  2.571, '6':  2.447,
  '7':  2.365, '8':  2.306, '9':  2.262, '10': 2.228, '11': 2.201, '12': 2.179,
  '13': 2.16,  '14': 2.145, '15': 2.131, '16': 2.12,  '17': 2.11,  '18': 2.101,
  '19': 2.093, '20': 2.086, '21': 2.08,  '22': 2.074, '23': 2.069, '24': 2.064,
  '25': 2.06,  '26': 2.056, '27': 2.052, '28': 2.048, '29': 2.045, '30': 2.042,
  'infinity': 1.96
};

function getCriticalValue(degreesOfFreedom) {
  return distribution[degreesOfFreedom] || distribution.infinity;
}

var marginOfError = standardError * getCriticalValue(sample.length - 1);
var relativeMarginOrError = (marginOfError / mean) * 100;

For reference here is how I handle all this stuff in Benchmark.js.

[jdalton]

Re: 4. This is by design, so that all the tests can be run in one block and timed that way. Trying to time single-run tests between setup periods is really inaccurate, and like I say I don't use it for DOM stuff. I mostly use the setup method to create some data structure before testing an operation on it, where I don't want the setup time of the data to factor into the test.

I wasn't suggesting you execute the setup() once per single test call. You should move the setup call to inside the "while (n--) {" loop and execute it just before the timer is started for that sample.

[jcoglan]

Thanks for the refresher course on statistics, very helpful. While I'm digesting it, some follow-up questions:

I understand the argument for determining run count based on getting the minimum to get you at least a 50ms runtime -- that gives that individual time measurement an error of 1%. But the runtime of a piece of code can be very variable, so you take many samples of this to get an estimate of the real value and its variance.

From what I understand, the strategy you're suggesting is:

• Let the 'task' be the fragment of code you want to benchmark, say new Foo()
• Find out how many times you need to run the task to get a measurement over 50ms
• Let this number be N, and let a 'run' be the act of executing the task N times
• Execute the run a fixed number of times, and take the mean and sample variance of these measurements
• Mean (estimated) runtime of the task is then equal to (sample mean / N)

Is this correct?

My understanding of the errors and confidence levels is still not clear though. I know if you take N measurements with error of 1% each, the error on the mean of these measurements is derived by adding the absolute errors up in quadrature and dividing this by N. However this doesn't capture the variance of the value you're measuring -- each measurement may have a high resolution, but the thing you're measuring is variable. Would appreciate some clarification if you have time (I really ought to know this but I've not used it for years, so I'm rusty).

About the environments -- the strategy you're proposing would still construct a batch of environments before a batch of tests, so if the test is tied to a singleton like the DOM, this doesn't solve your destructive update problem. Obviously setup time needs to be separated from the time for the test task, and each individual task execution will be too fast to measure accurately, so the tests must be batched. Can you have batched tests and destructive DOM updates at the same time?

[jcoglan]

I've removed the Benchmark module and will recommend people use benchmark.js instead -- it seems far more mature, works on a ton of platforms and there's not a strong reason to have this functionality in JS.Class. It's not anything related to the object system, collections, etc so it doesn't belong here.