Question: Singular Jacobian, probably redundant constraints

[ManuelZ]

I want to re-create the following mechanism in 3D: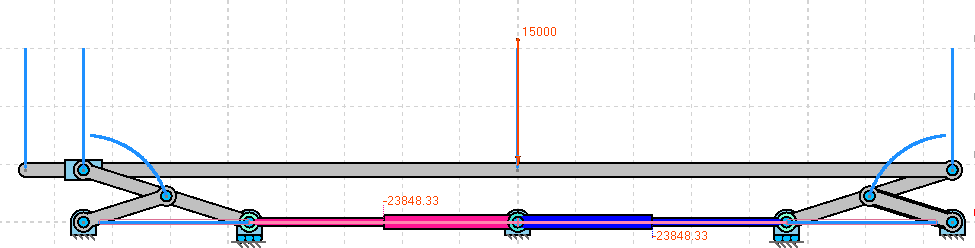

It's a double Scott-Russell mechanism which has, in addition to the sliding joints at the bottom, one sliding joint at the top, between the left large diagonal bar and the slider which is connected to the platform. (I think this way I get no redundant constraints in 2D? At least the software that I'm using stopped complaining after that).

I got this so far (in 3D):

Currently it's simulating like this (notice the disconnected bottom slider and the left large bar):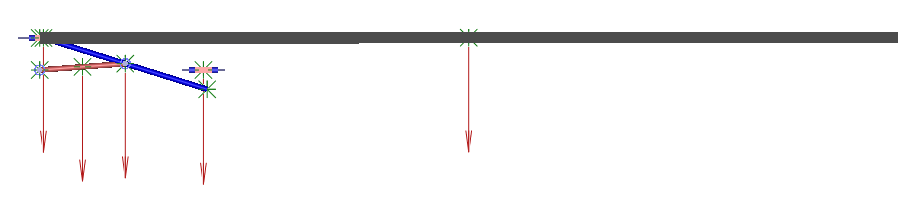

If I add a revolute joint between the bottom slider and the large bar, I get:

CSolverImplicitSecondOrder::InitializeSolverInitialConditions: System Jacobian seems to be singular / not invertible!The solver returned the causing system equation number (coordinate number) = 63
...

The causing system equation 63 belongs to a algebraic variable (Lagrange multiplier)
Potential object number(s) causing linear solver to fail: [10]
    object 10, name='object10', type=JointRevolute
...

ValueError: SolveDynamic terminated

Using either of these options allows me to continue the simulation: (but I guess the obtained forces and torques may end up varying across simulation runs?)

simulationSettings.linearSolverSettings.ignoreSingularJacobian = True
simulationSettings.linearSolverSettings.ignoreRedundantConstraints = True

I'm interpreting this problem as follows: some of the constraints added by this revolute joint end up being redundant with the ones added by the sliding joint that's present at the same location. The joints present at that point are these: a prismatic joint between the ground and the slider and a revolute joint between the slider and the left large bar.

AddPrismaticJoint(
    mbs,
    ground_object,
    slider_0_body_0,
    point=slider_bottom_point,
    axis=[1, 0, 0],
    useGlobalFrame=True,
)

AddRevoluteJoint(
   mbs,
   large_bar_body_0,
   slider_0_body_0,
   point=large_bar_bottom_body_point,
   axis=[0, 1, 0],
   useGlobalFrame=True, 
)

1) Am I correct into thinking that this may be he cause of the problem? What could I do to get around this? Maybe replacing one of those joints with a GenericJoint with less constraints?

2) Could I use ObjectKinematicTree here? I'm referring to it because I saw "closed loop mechanisms" in the ObjectKinematicTree documentation and sounded relevant.

I'm severely lacking theory here, sorry about that.

[ManuelZ]

I also saw the fourBarMechanismRedundant.py example file but couldn't figure out what was the gist of it. I see it as the classical example of when the Grübler–Kutzbach criterion fails, due to a redundant constraint, but I don't see anyting in particular that makes this example able to run without trouble. How can it run if there are redundancies?

[jgerstmayr]

the fourBarMechanismRedundant.py shows that some redundant joints can be considered. However, the limitations are currently such that the solver would need to perform full pivoting in order to extract all redundancies, which is currently not the case (but will be in the future). The only ways are: 1) use redundant formalism, but with GenericJoint at according places in order to avoid redundant constraints (basically you start with an open-loop system and as soon as you close loops - also to ground - you have to consider only those constraints, which are not causing a redundancy) 2) use KinematicTree for the open loop system and close loops in the same way as above

For simplicity, I recommend to use way 1). You can also use hard springs (e.g. CartesianSpringdamper) instead of some joints. In this way, you find out that the constraint redundancy is the main reason.

[ManuelZ]

Thank you very much. I tried with method 1 and with springs, and both worked easily.

I noticed that in mouseInteractionExample.py, ObjectConnectorCartesianSpringDamper is receiving MarkerBodyRigid markers instead of MarkerBodyPosition markers. Since the documentation says "the connector can be attached to position-based markers", I thought it was worth of mentioning, because it isn't clear to me if this is a mistake, or there is some inheritance going on, or something.

[jgerstmayr]

You are right about the markers: this looks to be confusing. The criterium for many connectors (or loads) is the existance of position information. Both, MarkerBodyPosition and MarkerBodyRigid provide position. Therefore, both markers can be used. MarkerBodyPosition may be alittle bit faster. I added a remark in MarkerBodyRigid and MarkerNodeRigid as well as in the general Marker section, see next update.