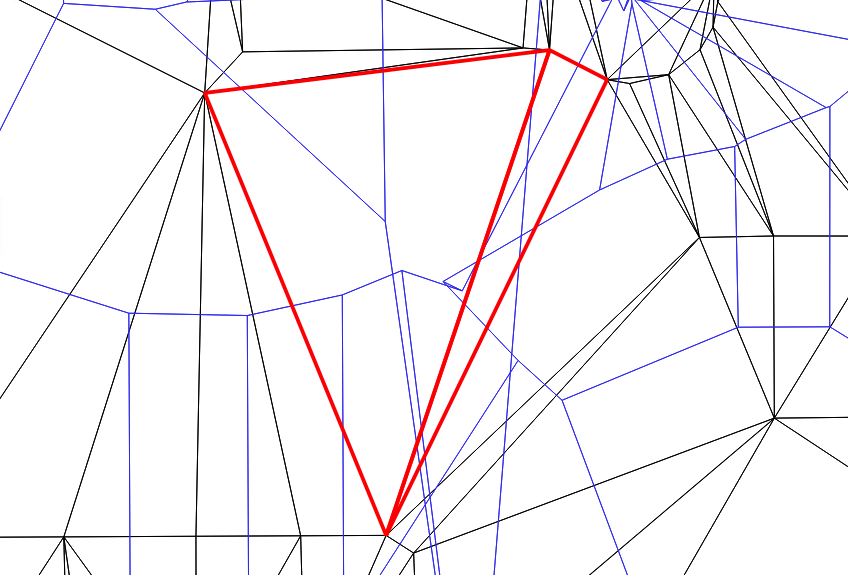
This shows the poly2tri triangulation in brown, overlaying a correctly formed Delaunay triangulation in red. In other words, where you see red, poly2tri is wrong

Open joycepg opened 6 years ago
This shows the poly2tri triangulation in brown, overlaying a correctly formed Delaunay triangulation in red. In other words, where you see red, poly2tri is wrong

Thanks for the explanation and the example :) I would be interested in solving this and I think the first thing to do would be to add some unit tests.
Also I have some reading to do about Delaunay triangulation, as I haven't written any of the code and certainly don't understand enough to make changes. Any papers you can recommend?
The way we triangulate is simply to calculate the extents of the input, extend by 1m in each direction to create an enclosing box for the CDT constructor, then add the input points, then triangulate.
Can you share the code or the data file for this?
thanks for the response.
I haven't written any of the code and certainly don't understand enough to make changes
good luck! it's pretty complex. i have written Delaunay triangulation routines in the past, and I found poly2tri pretty hard to follow.
this is a classic paper by Cline and Renka https://projecteuclid.org/download/pdf_1/euclid.rmjm/1250127667 it's also a good intro into the theory. but note it's a totally different algorithm to poly2tri.
Steven Fortune http://ect.bell-labs.com/who/sjf/ has a paper comparing four algorithms. http://ect.bell-labs.com/who/sjf/vddt.ps.gz i think poly2tri uses the plane-sweep
this is another, more recent, faster, algorithm http://www.s-hull.org
Can you share the code or the data file for this?
the data is attached in the original post. here's a snippet of code that might help
// calc entent of input points
for (size_t i=0; i<inputs.size(); i++) {
extent.merge(inputs[i].x, inputs[i].y);
}
// make a polyline of the extent boundary (extended a little bit to avoid duplicate points)
std::vector<p2t::Point*> polyline;
// use the vector of points to keep track of allocated storage
points.push_back(new p2t::Point(extent.getXmin() - 1.0, extent.getYmin() - 1.0));
polyline.push_back(points.back());
points.push_back(new p2t::Point(extent.getXmin() - 1.0, extent.getYmax() + 1.0));
polyline.push_back(points.back());
points.push_back(new p2t::Point(extent.getXmax() + 1.0, extent.getYmax() + 1.0));
polyline.push_back(points.back());
points.push_back(new p2t::Point(extent.getXmax() + 1.0, extent.getYmin() - 1.0));
polyline.push_back(points.back());
// create triangulation object
cdt = new p2t::CDT(polyline);
// add to vector of points (x,y) to keep track of allocated storage, and add pointers to them to the triangulation object
for (size_t i = 0; i< inputs.size(); i++) {
p2t::Point *px = new p2t::Point(inputs[i].x, inputs[i].y);
points.push_back(px);
cdt->AddPoint(px);
}
// triangulate
cdt->Triangulate();relevant bits of Extent class (pretty trivial)
Extent::Extent() {
this->xmin = HUGE_VAL;
this->ymin = HUGE_VAL;
this->xmax = -HUGE_VAL;
this->ymax = -HUGE_VAL;
}
// merge in a point to this extent
void Extent::merge(double x, double y) {
this->xmin = x<this->xmin ? x : this->xmin;
this->ymin = y<this->ymin ? y : this->ymin;
this->xmax = x>this->xmax ? x : this->xmax;
this->ymax = y>this->ymax ? y : this->ymax;
}Thanks for the links!
The paper and s-hull.org seem to be about triangulation of arbitrarily distributed points and not about triangulation of (concave) polygons with holes. How can I solve one problem with the other?
Steven Fortune http://ect.bell-labs.com/who/sjf/ has a paper comparing four algorithms. http://ect.bell-labs.com/who/sjf/vddt.ps.gz
I'm getting ERR_ADDRESS_UNREACHABLE on those links.
Regarding your code: What is the difference between inputs and shifts?
oops. inputs = shifts. i copied the code in, then edited it because i though "inputs" was a more obvious name for you. but i missed one. fixed.
a true Delaunay triangulation does not support holes, or concave shapes. it will always be bounded by the convex hull of the points, and interconnect all the points with triangles that are closest to equilateral as possible.
a constrained Delaunay triangulation can be constrained in a number of ways: a concave boundary, forcing certain edges (for example to preserve a real world edge such as a kerb line), or holes in the triangulation. some algorithms support both DT and CDT.
then there are completely non-Delaunay triangulations, that may also be concave, contain holes, etc.
that's so strange about the bell-labs URL. it's been there for years, and it was there on the day i put the comment in. now it's gone! the wayback machine is your friend :) https://web.archive.org/web/*/http://ect.bell-labs.com/who/sjf and https://web.archive.org/web/20161203100859/http://ect.bell-labs.com/who/sjf/vddt.ps.gz
Sorry for the late response, I've been busy with other stuff.
In small.txt why are there 4 numbers per line and not 2?
oh, a hangover from me modelling shifts. so:
x, y, dx, dy
you can ignore the dx,dy or use either of them for a 'z' value if you want to do interpolation off the TIN
I've added a function to check if a result is a valid Delaunay triangulation: https://github.com/jhasse/poly2tri/commit/0898bb217dd5e700ac78d07cbcb1e3257b8f5f1e#diff-2523d7c1103d8a1f18b73724e6a9f225R392 Does it look correct to you?
With your test set it returns false. But it also does with most of the files inside testbed/data ....
A constrained Delaunay triangulation may not be Delaunay so you wouldn't necessarily expect everything to pass that check even if it is correct. (The Constrained DT does not 'see' non-Delaunay vertices if they are across constraint edges.)
That said, these are also not exact checks due to floating point error. What I would do is try dropping Shewchuk's exact predicates ( https://github.com/danshapero/predicates ) into the code, and using them to make both CircumcicleContains and IsCounterClockwise robust. That may fix erroneous results outright, and it would also make your IsDelaunay check reliable ... (thought it would still not be a valid IsConstrainedDelaunay check)
Sorry it has been so long, I haven't had time to look at this again. Being realistic, I don't think I will any time soon. Here's my code if someone else wants to pick this issue up:
#include <boost/test/unit_test.hpp>
#include <poly2tri/poly2tri.h>
#include <iostream>
class Extent {
public:
/// merge in a point to this extent
void merge(const double x, const double y) {
xmax = x > xmax ? x : xmax;
xmin = x < xmin ? x : xmin;
ymax = y > ymax ? y : ymax;
ymin = y < ymin ? y : ymin;
}
double getXmax() const {
return xmax;
}
double getXmin() const {
return xmin;
}
double getYmax() const {
return ymax;
}
double getYmin() const {
return ymin;
}
private:
double xmax = std::numeric_limits<decltype(xmax)>::min();
double xmin = std::numeric_limits<decltype(xmin)>::max();
double ymax = std::numeric_limits<decltype(ymax)>::min();
double ymin = std::numeric_limits<decltype(ymin)>::max();
};
BOOST_AUTO_TEST_CASE(Issue4Test) {
std::vector<p2t::Point> inputs{
{ 265.410, 373.015 }, { 27.965, 394.280 }, { 35.315, 394.980 }, { 46.358, 396.032 },
{ 57.986, 396.059 }, { 111.815, 396.183 }, { 134.175, 396.234 }, { 156.841, 396.286 },
{ 184.063, 396.349 }, { 221.369, 393.714 }, { 240.132, 392.380 }, { 258.364, 391.083 },
{ 276.189, 389.815 }, { 281.351, 389.448 }, { 285.571, 389.836 }, { 289.235, 391.548 },
{ 293.032, 392.941 }, { 295.406, 393.122 }, { 56.181, 379.188 }, { 84.424, 378.422 },
{ 113.439, 378.303 }, { 136.215, 378.210 }, { 159.927, 378.113 }, { 189.119, 378.273 },
{ 206.354, 377.085 }, { 226.479, 375.698 }, { 246.382, 374.326 }, { 282.861, 370.598 },
{ 286.758, 367.072 }, { 287.616, 364.871 }, { 263.523, 342.119 }, { 337.969, 351.647 },
{ 307.459, 351.960 }, { 337.656, 184.681 }, { 337.583, 145.461 }, { 337.830, 277.351 },
{ 307.637, 276.239 }, { 395.443, 91.112 }, { 397.746, 21.017 }, { 397.472, 39.641 },
{ 398.279, 91.146 }, { 395.508, 119.829 }, { 219.938, 260.551 }, { 30.778, 171.230 },
{ 0.000, 143.257 }, { 27.207, 145.090 }, { 29.285, 147.088 }, { 30.448, 149.726 },
{ 30.680, 154.024 }, { 30.917, 195.831 }, { 31.049, 219.025 }, { 31.162, 238.972 },
{ 31.424, 285.064 }, { 0.139, 171.404 }, { 118.513, 80.839 }, { 119.130, 39.958 },
{ 113.484, 80.716 }, { 175.680, 91.165 }, { 175.652, 0.000 }, { 175.663, 35.013 },
{ 174.510, 120.502 }, { 137.441, 202.145 }, { 144.173, 209.437 }, { 193.925, 210.133 },
{ 198.629, 209.755 }, { 208.854, 204.501 }, { 212.831, 203.811 }, { 219.762, 205.391 },
{ 225.328, 209.816 }, { 227.637, 213.810 }, { 228.488, 218.344 }, { 228.344, 220.558 },
{ 227.844, 222.719 }, { 225.962, 227.934 }, { 222.056, 231.868 }, { 218.169, 233.816 },
{ 213.949, 234.858 }, { 209.904, 234.351 }, { 206.108, 232.865 }, { 203.051, 231.437 },
{ 200.061, 229.875 }, { 197.696, 229.061 }, { 195.343, 228.213 }, { 143.379, 227.948 },
{ 139.260, 230.606 }, { 155.335, 91.065 }, { 135.942, 90.970 }, { 136.430, 34.720 },
{ 238.369, 176.763 }, { 238.514, 144.445 }, { 258.346, 176.749 }, { 225.227, 176.498 },
{ 123.618, 315.879 }, { 84.653, 343.945 }, { 113.282, 344.059 }, { 136.682, 344.152 },
{ 160.081, 344.245 }, { 117.935, 290.077 }, { 117.175, 292.983 }, { 114.819, 298.238 },
{ 113.898, 300.811 }, { 114.070, 305.468 }, { 115.631, 309.858 }, { 118.336, 313.125 },
{ 125.845, 316.360 }, { 129.824, 316.087 }, { 133.241, 314.939 }, { 136.541, 313.487 },
{ 139.900, 312.404 }, { 170.345, 260.552 }, { 186.048, 344.348 }, { 162.628, 251.082 },
{ 162.591, 271.119 }, { 182.183, 260.289 }, { 84.704, 228.601 }, { 49.003, 228.923 },
{ 257.979, 268.670 }, { 288.583, 268.854 }, { 257.426, 291.679 }, { 257.887, 259.303 },
{ 337.933, 332.428 }, { 307.506, 331.867 }, { 84.581, 123.243 }, { 169.637, 123.637 },
{ 154.468, 123.567 }, { 135.886, 123.481 }, { 112.438, 123.372 }, { 84.547, 80.266 },
};
Extent extent;
// calc entent of input points
for (size_t i = 0; i < inputs.size(); i++) {
extent.merge(inputs[i].x, inputs[i].y);
}
// make a polyline of the extent boundary (extended a little bit to avoid duplicate points)
std::vector<p2t::Point*> polyline;
std::vector<p2t::Point*> points;
// use the vector of points to keep track of allocated storage
points.push_back(new p2t::Point(extent.getXmin() - 1.0, extent.getYmin() - 1.0));
polyline.push_back(points.back());
points.push_back(new p2t::Point(extent.getXmin() - 1.0, extent.getYmax() + 1.0));
polyline.push_back(points.back());
points.push_back(new p2t::Point(extent.getXmax() + 1.0, extent.getYmax() + 1.0));
polyline.push_back(points.back());
points.push_back(new p2t::Point(extent.getXmax() + 1.0, extent.getYmin() - 1.0));
polyline.push_back(points.back());
// create triangulation object
p2t::CDT cdt(polyline);
// add to vector of points (x,y) to keep track of allocated storage, and add pointers to them to
// the triangulation object
for (size_t i = 0; i < inputs.size(); i++) {
p2t::Point* px = new p2t::Point(inputs[i].x, inputs[i].y);
points.push_back(px);
cdt.AddPoint(px);
}
// triangulate
cdt.Triangulate();
const auto triangles = cdt.GetTriangles();
BOOST_CHECK(IsDelaunay(triangles));
}I made a rust porting of this lib. While porting, I also met the problem, the result is not valid delaunay (not because of constrained edge), I nailed it down and fixed in my port. I recall it has something to do with the "delaunay" edge flag, which doesn't cleaned/maintained properly.
FYI: this is the port, if anyone interested: https://github.com/shuoli84/poly2tri-rs
Hi, In using this library, we noticed some differences from another (proprietary) triangulation library that was builtin to some software we were using. Further investigation has revealed that poly2tri does not produce a valid Delaunay triangulation. We do not use holes or any constraints. I'm pretty sure this is the issue that is referred to here https://github.com/greenm01/poly2tri/issues/48 which was never solved. The last thing the maintainer said was "This issue needs some deeper analysis." Is there any interest in solving this?
This data file of 128 points illustrates the problem small.txt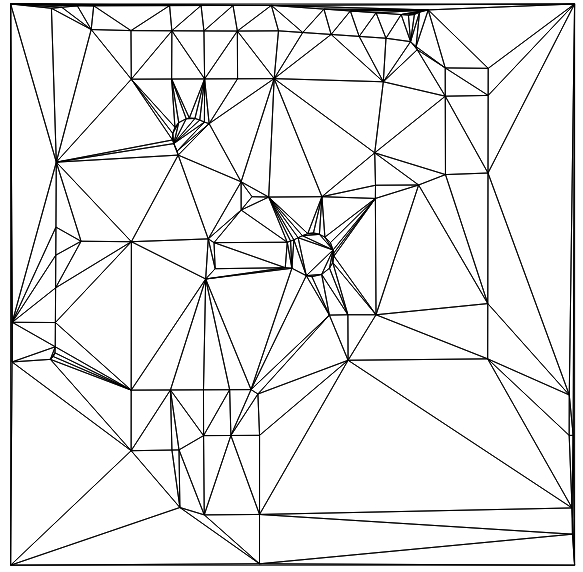
The way we triangulate is simply to calculate the extents of the input, extend by 1m in each direction to create an enclosing box for the CDT constructor, then add the input points, then triangulate. geojson file of the triangles In this result, triangles with id=32 and id=33 are non-Delaunay. These are roughly in the centre of the overview image above.
The error is completely obvious when the dual of the triangulation (the Voronoi polygons) is calculated - you get bow ties in the polygons