Optimize corr_matrix() performance

[XD-DENG]

Correlation matrix has two important properties:

• it is a symmetric matrix (corr(i, j) == corr(j, i))
• the entries on the main diagonal are always 1.0 (corr(i, i) == 1.0)

These two properties can help reduce the times of invoking DF.corr() from n^2 to (n^2-n)/2 (cut by more than half).

Say there are 100 columns. The current implementation in master branch will need to call DF.corr() for 10,000 times, while my code can help reduce this number to 4,950.

Visualize the Idea

Blue cells indicate the entries for which invoking DF.corr() is required.

Green cells indicate the entries for which we don't have to invoke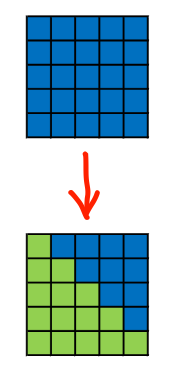 DF.corr() due to the properties of correlation matrix.

[XD-DENG]

Hi @julioasotodv , mind taking a look? Let me know if any clarification is needed. Cheers.

[julioasotodv]

Indeed, you are totally right.

Merging. Thank you very much!