Why concorde solver give me a tour which is not optimal?

[XiaoshanLin9701]

I wonder why concorde give me tours which are obviously not optimal. Also the optimal value given by concorde doesn't equal to the actual length of the tour. Anybody can help me with this?

[jvkersch]

@XiaoshanLin9701 Thanks for the report, this is interesting. Could you post the coordinates for the problem in the graph you posted?

[cm8908]

Hello @jvkersch I also encountered a same situation that solved tour is not optimal Here is my coordinates of TSP size 50 and concorde output solution.

[[0.5450, 0.3881], [0.6699, 0.1855], [0.3697, 0.7256], [0.7606, 0.3439], [0.9684, 0.9490], [0.7757, 0.8813], [0.5889, 0.3956], [0.7995, 0.4281], [0.5556, 0.8681], [0.7107, 0.2210], [0.3930, 0.6308], [0.1932, 0.0714], [0.0134, 0.8377], [0.3791, 0.8158], [0.3263, 0.4226], [0.2342, 0.8151], [0.6011, 0.7030], [0.2287, 0.9683], [0.0966, 0.6221], [0.0657, 0.4010], [0.7254, 0.0392], [0.9949, 0.9556], [0.4600, 0.3212], [0.3056, 0.9393], [0.1407, 0.3770], [0.7613, 0.2029], [0.5116, 0.4894], [0.8031, 0.7751], [0.1035, 0.8477], [0.4515, 0.4389], [0.8378, 0.6296], [0.7580, 0.3678], [0.8141, 0.0437], [0.8185, 0.8778], [0.9941, 0.9753], [0.0475, 0.4393], [0.3862, 0.0921], [0.8152, 0.1016], [0.3587, 0.3812], [0.2048, 0.2656], [0.9384, 0.7618], [0.0842, 0.0578], [0.1371, 0.5424], [0.5628, 0.8304], [0.2784, 0.6911], [0.6381, 0.7200], [0.4481, 0.0412], [0.5601, 0.1288], [0.8831, 0.5668], [0.9034, 0.3343]]

ComputedTour(tour=array([ 0, 38, 47, 25, 1, 9, 48, 4, 5, 40, 30, 34, 21, 33, 43, 13, 23, 16, 27, 6, 10, 44, 22, 39, 24, 15, 18, 42, 14, 29, 35, 41, 46, 11, 19, 12, 28, 17, 8, 2, 26, 7, 45, 3, 49, 32, 37, 20, 36, 31], dtype=int32), optimal_value=0.0, success=True, found_tour=True, hit_timebound=False)

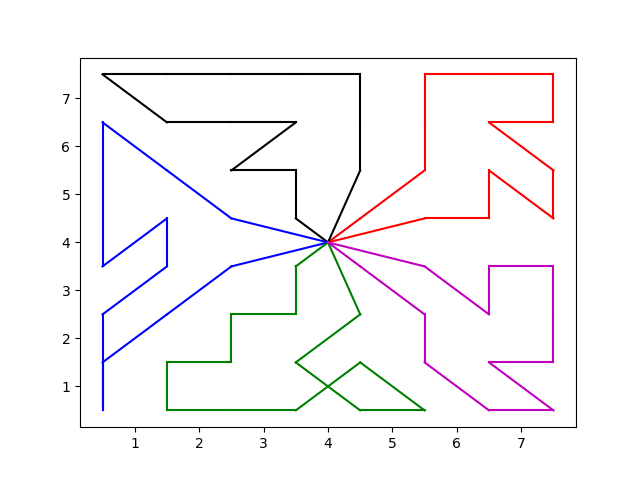
And visualization of this is:

I ran the following code to get solution

from concorde.tsp import TSPSolver
# example is a numpy ndarray containing 2d coordinates of shape (50, 2)
solver = TSPSolver.from_data(example[:,0], example[:,1], norm='EUC_2D')
solution = solver.solve()

[cm8908]

Hello @jvkersch I also encountered a same situation that solved tour is not optimal Here is my coordinates of TSP size 50 and concorde output solution.

[[0.5450, 0.3881], [0.6699, 0.1855], [0.3697, 0.7256], [0.7606, 0.3439], [0.9684, 0.9490], [0.7757, 0.8813], [0.5889, 0.3956], [0.7995, 0.4281], [0.5556, 0.8681], [0.7107, 0.2210], [0.3930, 0.6308], [0.1932, 0.0714], [0.0134, 0.8377], [0.3791, 0.8158], [0.3263, 0.4226], [0.2342, 0.8151], [0.6011, 0.7030], [0.2287, 0.9683], [0.0966, 0.6221], [0.0657, 0.4010], [0.7254, 0.0392], [0.9949, 0.9556], [0.4600, 0.3212], [0.3056, 0.9393], [0.1407, 0.3770], [0.7613, 0.2029], [0.5116, 0.4894], [0.8031, 0.7751], [0.1035, 0.8477], [0.4515, 0.4389], [0.8378, 0.6296], [0.7580, 0.3678], [0.8141, 0.0437], [0.8185, 0.8778], [0.9941, 0.9753], [0.0475, 0.4393], [0.3862, 0.0921], [0.8152, 0.1016], [0.3587, 0.3812], [0.2048, 0.2656], [0.9384, 0.7618], [0.0842, 0.0578], [0.1371, 0.5424], [0.5628, 0.8304], [0.2784, 0.6911], [0.6381, 0.7200], [0.4481, 0.0412], [0.5601, 0.1288], [0.8831, 0.5668], [0.9034, 0.3343]]

ComputedTour(tour=array([ 0, 38, 47, 25, 1, 9, 48, 4, 5, 40, 30, 34, 21, 33, 43, 13, 23, 16, 27, 6, 10, 44, 22, 39, 24, 15, 18, 42, 14, 29, 35, 41, 46, 11, 19, 12, 28, 17, 8, 2, 26, 7, 45, 3, 49, 32, 37, 20, 36, 31], dtype=int32), optimal_value=0.0, success=True, found_tour=True, hit_timebound=False)

And visualization of this is:

I ran the following code to get solution

from concorde.tsp import TSPSolver
# example is a numpy ndarray containing 2d coordinates of shape (50, 2)
solver = TSPSolver.from_data(example[:,0], example[:,1], norm='EUC_2D')
solution = solver.solve()

It has something to do with the norm argument. I solved it by setting it to 'GEO'!

[chkwon]

See https://github.com/jvkersch/pyconcorde/issues/29

Multiplying a large constant, say 1000, to the coordinates would resolve the issue.

[XiayangLi2301]

Setting it to the GEO