// 1st way => O(2^n)
/*-----------------------Brute Force way ---------------*/
int fibo(int n) {
if(n <= 1) {
return n;
}
int a = fibo(n - 1);
int b = fibo(n - 2);
return a + b;
}
// 2nd Way => O(n) but space complexity high cz of recursion
/*-----------------------Memoization(Recursion) (Top - Down) ---------------*/
int fibo_helper(int n, int *ans) {
if(n <= 1) {
return n;
}
// Check if output already exists
if(ans[n] != -1) {
return ans[n];
}
// Calculate output
int a = fibo_helper(n-1, ans);
int b = fibo_helper(n-2, ans);
// Save the output for future use
ans[n] = a + b;
// Return the final output
return ans[n];
}
int fibo_2(int n) {
int *ans = new int[n+1];
for(int i = 0; i <= n; i++) {
ans[i] = -1;
}
return fibo_helper(n, ans);
}
Fibonacci - 2
// 3rd way => O(n) with best space complexity
/*-----------------------using DP (Iterative ) (Bottom- UP) ---------------*/
int fibo_3(int n) {
int *ans = new int[n+1];
ans[0] = 0;
ans[1] = 1;
for(int i = 2; i <= n; i++) {
ans[i] = ans[i-1] + ans[i-2];
}
return ans[n];
}
Code : Min Steps to 1
Given a positive integer 'n', find and return the minimum number of steps that 'n' has to take to get reduced to 1. You can perform any one of the following 3 steps:
1.) Subtract 1 from it. (n = n - 1) ,
2.) If its divisible by 2, divide by 2.( if n % 2 == 0, then n = n / 2 ) ,
3.) If its divisible by 3, divide by 3. (if n % 3 == 0, then n = n / 3 ).
Write brute-force recursive solution for this.
Input format :
The first and the only line of input contains an integer value, 'n'.
Output format :
Print the minimum number of steps.
Constraints :
1 <= n <= 200
Time Limit: 1 sec
Sample Input 1 :
4
Sample Output 1 :
2
Explanation of Sample Output 1 :
For n = 4
Step 1 : n = 4 / 2 = 2
Step 2 : n = 2 / 2 = 1
Sample Input 2 :
7
Sample Output 2 :
3
Explanation of Sample Output 2 :
For n = 7
Step 1 : n = 7 - 1 = 6
Step 2 : n = 6 / 3 = 2
Step 3 : n = 2 / 2 = 1
#include <bits/stdc++.h>
using namespace std;
/*
Time Complexity : O(3^N)
Space Complexity : O(N)
where N is the given positive integer
*/
#include <climits>
int countMinStepsToOne(int n)
{
// Base case
if(n <= 1) {
return 0;
}
// Recursive call
int subtractOne = countMinStepsToOne(n - 1);
int divideByTwo = INT_MAX;
int divideByThree = INT_MAX;
if (n % 2 == 0)
{
divideByTwo = countMinStepsToOne(n / 2);
}
if (n % 3 == 0)
{
divideByThree = countMinStepsToOne(n / 3);
}
// Calculate final output
int ans = 1 + min(subtractOne, min(divideByTwo, divideByThree));
return ans;
}
int main()
{
int n;
cin >> n;
cout << countMinStepsToOne(n);
}
Code : Min Steps to 1 using DP && Solution
Code : Min Steps to 1 using DP
Given a positive integer 'n', find and return the minimum number of steps that 'n' has to take to get reduced to 1. You can perform any one of the following 3 steps:
1.) Subtract 1 from it. (n = n - 1) ,
2.) If n is divisible by 2, divide by 2.( if n % 2 == 0, then n = n / 2 ) ,
3.) If n is divisible by 3, divide by 3. (if n % 3 == 0, then n = n / 3 ).
Input format :
The first and the only line of input contains an integer value, 'n'.
Output format :
Print the minimum number of steps.
Constraints :
1 <= n <= 10 ^ 6
Time Limit: 1 sec
Sample Input 1 :
4
Sample Output 1 :
2
Explanation of Sample Output 1 :
For n = 4
Step 1 : n = 4 / 2 = 2
Step 2 : n = 2 / 2 = 1
Sample Input 2 :
7
Sample Output 2 :
3
Explanation of Sample Output 2 :
For n = 7
Step 1 : n = 7 - 1 = 6
Step 2 : n = 6 / 3 = 2
Step 3 : n = 2 / 2 = 1
/*--------------------------------1st Approach----------------------------*/
#include <bits/stdc++.h>
using namespace std;
/*
Time Complexity : O(n)
Space Complexity : O(n)
*/
int countStepsToOne(int n)
{
int *minSteps = new int[n + 1];
minSteps[1] = 0;
for (int i = 2; i <= n; ++i)
{
int subtractOne = minSteps[i - 1];
int divideByTwo = INT_MAX;
int divideByThree = INT_MAX;
if (i % 2 == 0)
{
divideByTwo = minSteps[i / 2];
}
if (i % 3 == 0)
{
divideByThree = minSteps[i / 3];
}
minSteps[i] = 1 + min(subtractOne, min(divideByTwo, divideByThree));
}
int result = minSteps[n];
delete[] minSteps;
return result;
}
int main()
{
int n;
cin >> n;
cout << countStepsToOne(n);
}
/*--------------------------------------2nd Approach-------------------------------------------*/
#include <bits/stdc++.h>
using namespace std;
/*
Time Complexity : O(n)
Space Complexity : O(n)
*/
int minStepsHelper(int n, int *ans) {
// Base case
if(n <= 1) {
return 0;
}
// Check if output already exists
if(ans[n] != -1) {
return ans[n];
}
// Calculate output
int subtractOne = minStepsHelper(n - 1, ans);
int divideByTwo = INT_MAX, divideByThree = INT_MAX;
if(n % 2 == 0) {
divideByTwo = minStepsHelper(n/2, ans);
}
if(n % 3 == 0) {
divideByThree = minStepsHelper(n/3, ans);
}
int output = min(subtractOne, min(divideByTwo, divideByThree)) + 1;
// Save output for future use
ans[n] = output;
return output;
}
int countStepsToOne_2ndApproach(int n) {
int *ans = new int[n+1];
for(int i = 0; i <= n; i++) {
ans[i] = -1;
}
return minStepsHelper(n, ans);
}
int main()
{
int n;
cin >> n;
cout << countStepsToOne_2ndApproach(n);
}
Code : Staircase using Dp and Solutions
Code : Staircase using Dp
A child is running up a staircase with n steps and can hop either 1 step, 2 steps or 3 steps at a time. Implement a method to count how many possible ways the child can run up to the stairs. You need to return all possible number of ways.
Time complexity of your code should be O(n).
Since the answer can be pretty large print the answer % mod(10^9 +7)
Input Format:
First line will contain T (number of test case).
Each test case is consists of a single line containing an integer N.
Output Format:
For each test case print the answer in new line
Constraints :
1 <= T < = 10
1 <= N <= 10^5
Sample input 1
2
2
3
Sample output 1
2
4
Explanation of sample input 1:
Test case 1:
To reach at top of 2nd stair, we have only two options i.e (2), (1,1)
Test case 2:
To reach at top of 3rd stair, we have four options i.e (1,1,1), (1,2) ,(2,1), (3)
Sample input 2:
2
5
10
Sample output 2:
13
274
#include <bits/stdc++.h>
using namespace std;
long long mod = 1e9 + 7;
/*Time complexity: O(N)
Space complexity: O(1)
Where N is the input given
*/
int stairCase(int n)
{
long *ans = new long[n + 1];
ans[0] = 1;
ans[1] = 1;
ans[2] = 2;
for (int i = 3; i <= n; ++i)
{
ans[i] = (ans[i - 1] + ans[i - 2] + ans[i - 3]) % mod;
}
return ans[n] % mod;
}
int main()
{
int t;
cin >> t;
while (t--)
{
int n;
cin >> n;
cout << stairCase(n) << endl;
}
}
Code : Minimum Count & Solution
Code : Minimum Count
Given an integer N, find and return the count of minimum numbers required to represent N as a sum of squares.
That is, if N is 4, then we can represent it as : {1^2 + 1^2 + 1^2 + 1^2} and {2^2}. The output will be 1, as 1 is the minimum count of numbers required to represent N as sum of squares.
Input format :
The first and the only line of input contains an integer value, 'N'.
Output format :
Print the minimum count of numbers required.
Constraints :
0 <= n <= 10 ^ 4
Time Limit: 1 sec
Sample Input 1 :
12
Sample Output 1 :
3
Explanation of Sample Output 1 :
12 can be represented as :
A) (1^2) + (1^2) + (1^2) + (1^2) + (1^2) + (1^2) + (1^2) + (1^2) + (1^2) + (1^2) + (1^2) + (1^2)
B) (1^2) + (1^2) + (1^2) + (1^2) + (1^2) + (1^2) + (1^2) + (1^2) + (2 ^ 2)
C) (1^2) + (1^2) + (1^2) + (1^2) + (2 ^ 2) + (2 ^ 2)
D) (2 ^ 2) + (2 ^ 2) + (2 ^ 2)
As we can see, the output should be 3.
Sample Input 2 :
9
Sample Output 2 :
1
#include <bits/stdc++.h>
using namespace std;
/*Time Complexity : O(n* sqrt(n))
Space Complexity : O(n)
*/
int minCount(int n)
{
int *minSquaresRequired = new int[n + 1];
minSquaresRequired[0] = 0;
minSquaresRequired[1] = 1;
for (int i = 2; i <= n; ++i)
{
minSquaresRequired[i] = INT_MAX;
for (int j = 1; i - (j *j) >= 0; ++j)
{
minSquaresRequired[i] = min(minSquaresRequired[i], minSquaresRequired[i - (j *j)]);
}
minSquaresRequired[i] += 1;
}
int result = minSquaresRequired[n];
delete[] minSquaresRequired;
return result;
}
int main()
{
int n;
cin >> n;
cout << minCount(n);
}
Code : No. of balanced BTs and Solutions using Recursion
Code : No. of balanced BTs using Recursion
Given an integer h, find the possible number of balanced binary trees of height h. You just need to return the count of possible binary trees which are balanced.
This number can be huge, so, return output modulus 10^9 + 7.
Write a simple recursive solution.
Input Format :
The first and only line of input contains an integer, that denotes the value of h. Here, h is the height of the tree.
Output Format :
The first and only line of output contains the count of balanced binary trees modulus 10^9 + 7.
Constraints :
1 <= h <= 24
Time Limit: 1 sec
Sample Input 1:
3
Sample Output 1:
15
Sample Input 2:
4
Sample Output 2:
315
#include <iostream>
using namespace std;
/*Time complexity: O(2^N)
Space complexity: O(N)
where N is the final height of the binary tree
*/
int balancedBTs(int n)
{
if (n <= 1)
{
return 1;
}
int mod = 1e9 + 7;
int x = balancedBTs(n - 1);
int y = balancedBTs(n - 2);
long long int temp1 = ((long long int) x *x) % mod; // Number of BTs made by attaching subtrees of height (n - 1) at both sides of root
long long int temp2 = (2 *(long long int) x *y) % mod; // Number of BTs made by attaching subtrees of heights (n - 1) and (n - 2) at each side of root
long long int ans = (temp1 + temp2) % mod;
return ans;
}
int main() {
int n;
cin >> n;
cout << balancedBTs(n);
}
Code : No. of balanced BTs and Solutions using DP
Code : No. of balanced BTs using DP
Given an integer h, find the possible number of balanced binary trees of height h. You just need to return the count of possible binary trees which are balanced.
This number can be huge, so, return output modulus 10^9 + 7.
Time complexity should be O(h).
Input Format :
The first and only line of input contains an integer, that denotes the value of h. Here, h is the height of the tree.
Output Format :
The first and only line of output contains the count of balanced binary trees modulus 10^9 + 7.
Constraints :
1 <= h <= 10^6
Time Limit: 1 sec
Sample Input 1:
3
Sample Output 1:
15
Sample Input 2:
4
Sample Output 2:
315
#include <iostream>
using namespace std;
/*Time complexity: O(N)
Space complexity: O(N)
where N is the final height of the binary tree
*/
#include <vector>
int balancedBTs(int n)
{
vector < long long int > dp(n + 1); // dp[i] represents number of balanced BTs of height i
if (n <= 1)
{
return 1;
}
dp[0] = 1;
dp[1] = 1;
int mod = 1e9 + 7;
for (int i = 2; i <= n; ++i)
{
long long int temp1 = dp[i - 1] *dp[i - 1];
temp1 = temp1 % mod;
long long int temp2 = 2 *dp[i - 1] *dp[i - 2];
temp2 = temp2 % mod;
dp[i] = (temp1 + temp2) % mod;
}
return dp[n];
}
int main() {
int n;
cin >> n;
cout << balancedBTs(n);
}
Lecture 18 : DP - 1
//============>>>>>>>>>> Lecture 18 : DP - 1 Notes Lecture 18 : DP - 1 Notes.pdf
Fibonacci - 1
Fibonacci - 2
Code : Min Steps to 1 Question AND Solution
https://youtu.be/LK55EnLwMzA
Code : Min Steps to 1 using DP && Solution
/--------------------------------------2nd Approach-------------------------------------------/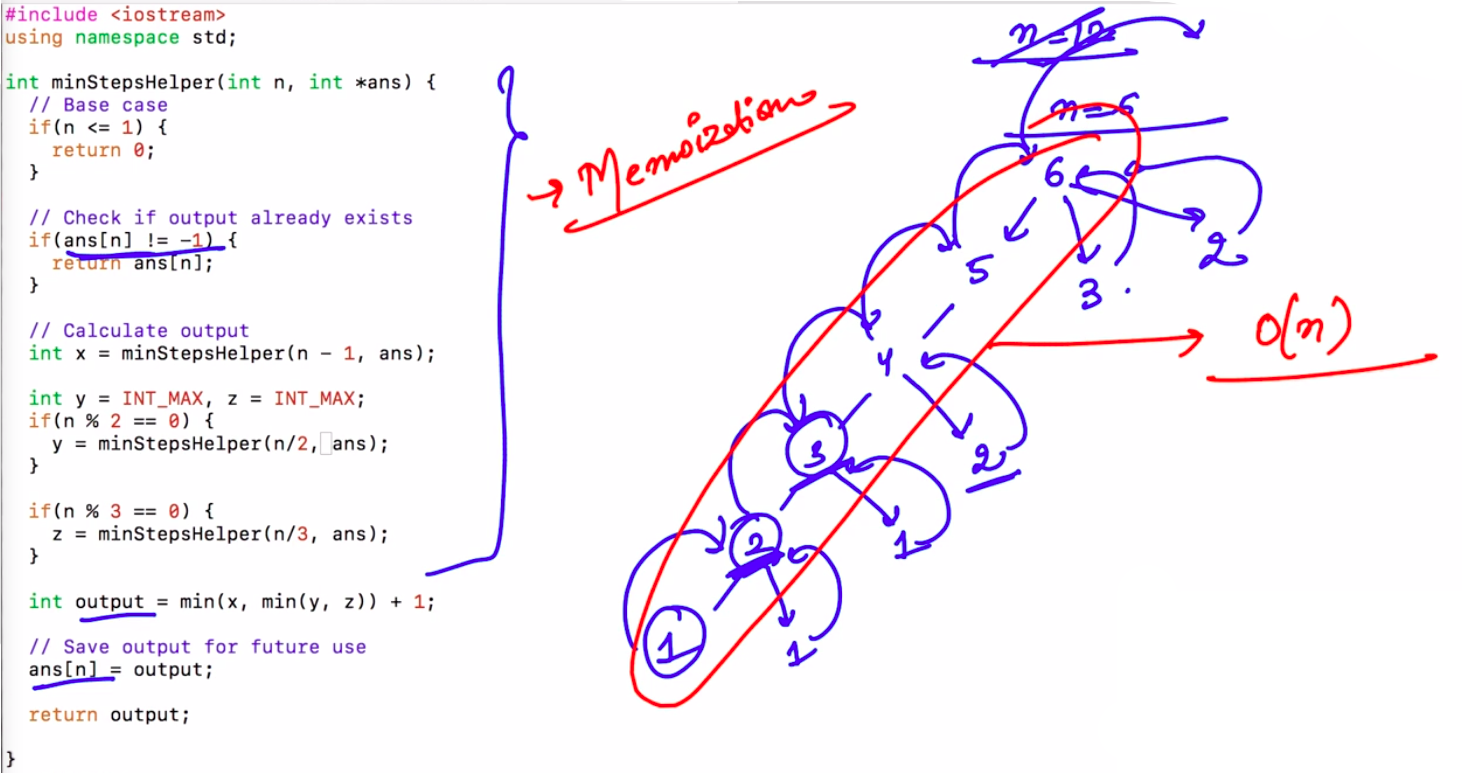
Code : Staircase using Dp and Solutions
Code : Minimum Count & Solution
Code : No. of balanced BTs and Solutions using Recursion
https://youtu.be/pyO2FJE7G9o
https://youtu.be/H1qjjkm3P3c
Code : No. of balanced BTs and Solutions using DP