Quadratic slowdown with nested control effect

[jasigal]

The problem

The following Koka code is quadratic w.r.t. iters:

pub module quadratic

import std/os/env
import std/text/parse

effect ctl inc() : int

fun work(iters)
  var acc := 0
  repeat(iters) {acc := (acc + inc())}
  acc

fun main()
  val iters = try {get-args().head.unjust.parse-int.unjust} fn(_) {100}
  with ctl inc() resume(1)
  with ctl inc() resume(inc() + 1)
  println(work(iters))

see this graph and quadratic-results.txt which was produced with the hyperfine program. Furthermore, if I take iters too high, for example 100,000, I get a segmentation fault. This can increased by increasing the stack size via ulimit, so I imagine the issue is that the stack space is exceeded.

Some solutions

I have found two ways to alleviate this. The first is to change the effect from ctl to fun, i.e.

pub module linear

import std/os/env
import std/text/parse

effect fun inc() : int

fun work(iters)
  var acc := 0
  repeat(iters) {acc := (acc + inc())}
  acc

fun main()
  val iters = try {get-args().head.unjust.parse-int.unjust} fn(_) {100}
  with fun inc() 1
  with fun inc() inc() + 1
  println(work(iters))

which results in the following graph and linear-results.txt. The second solution is to move the outer handler into the inner handler, i.e

pub module linear-ctl

import std/os/env
import std/text/parse

effect ctl inc() : int

fun work(iters)
  var acc := 0
  repeat(iters) {acc := (acc + inc())}
  acc

fun main()
  val iters = try {get-args().head.unjust.parse-int.unjust} fn(_) {100}
  with ctl inc()
    val r =
      with ctl inc() resume(1)
      inc() + 1
    resume(r)
  println(work(iters))

which results in the following graph and linear-results-ctl.txt.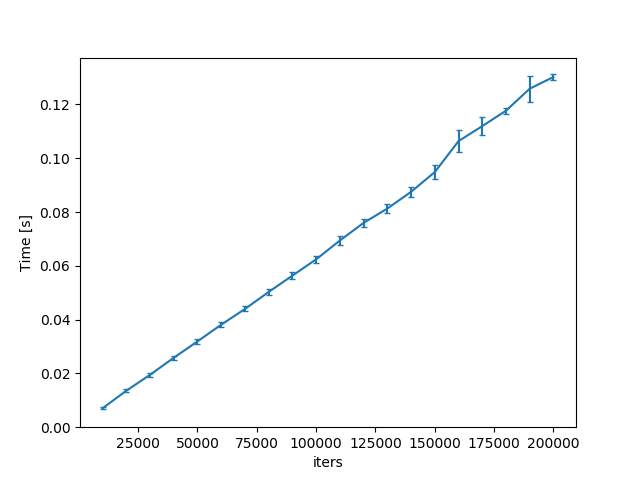

A comparison

I don't think this quadratic behaviour is intrinsically necessary. The following is (hopefully) an equivalent Frank progam to quadratic

interface Inc = inc : Int

work : Int -> Ref Int -> [RefState, Inc] Int
work 0 acc = read acc
work iters acc =
    write acc (read acc + inc!);
    work (iters - 1) acc

inner : <Inc> X -> [Inc] X
inner x = x
inner <inc -> k> = let r = inc! + 1 in inner (k r)

outer : <Inc> X -> X
outer x = x
outer <inc -> k> = outer (k 1)

t1000 : {[RefState] Int}
t1000! = let r = new 0 in outer (inner (work 1000 r))

t2000 : {[RefState] Int}
t2000! = let r = new 0 in outer (inner (work 2000 r))

t3000 : {[RefState] Int}
t3000! = let r = new 0 in outer (inner (work 3000 r))

t4000 : {[RefState] Int}
t4000! = let r = new 0 in outer (inner (work 4000 r))

t5000 : {[RefState] Int}
t5000! = let r = new 0 in outer (inner (work 5000 r))

t6000 : {[RefState] Int}
t6000! = let r = new 0 in outer (inner (work 6000 r))

t7000 : {[RefState] Int}
t7000! = let r = new 0 in outer (inner (work 7000 r))

t8000 : {[RefState] Int}
t8000! = let r = new 0 in outer (inner (work 8000 r))

t9000 : {[RefState] Int}
t9000! = let r = new 0 in outer (inner (work 9000 r))

t10000 : {[RefState] Int}
t10000! = let r = new 0 in outer (inner (work 10000 r))

which results in the following graph and quadratic-frank-results.txt.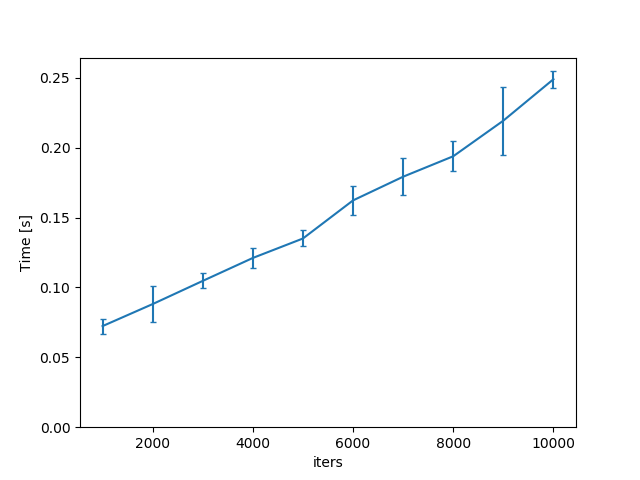

Comments

The reason I care and want this is I'm implementing automatic differentiation in Koka after doing it in Frank. I found that having multiple versions of the same effect and nesting handlers as above is useful, and I can't mark the effect as fun because reverse mode AD requires ctl. I also don't want to use the second solution because I lose compositionality (or at the very least I need to change the design).

[TimWhiting]

The example does not actually use non-linear control, so in this case I would hope that Koka compiles it directly to a linear handler even though it is marked ctl. Apparently it does not? Frank might be doing a similar optimization. So this benchmark might be testing the ability to optimize linear behavior rather than actually testing non-linear behavior. To get a good benchmark comparison consider creating an example with actual non-linear control characteristics.

[jasigal]

Re: optimizing to linear, Frank pretty much does no optimizations AFAIK.

Re: benchmark which uses non-linear control, here is a graph I already have from my thesis for reverse mode automatic differentiation. It runs code in the handler after a resumed continuation.

which shows the sames quadratic behaviour using Koka 2.4.0. Here's a gist of the code, the reverse-taylor-recip-benchmark.kk is the program being to produce the graph. If that's too verbose, I can try to make a smaller example.

So I'd say there are two bugs

• control effects which should be optimized and aren't; and
• unnecessary slowdowns for some non-linear control flow.

[TimWhiting]

I don't know if you knew this, but you can keep the effect definition functions as ctl and use the more restrictive fun when writing the handler functions for the effect.

Doing this for all of the tail resumptive clauses results in the above graph.

Knowing what I know about how Koka implements handlers I would say that the first bug you mention actually is causing the second bug.

Fortunately it is easy for a user to fix now, and with better analysis, Koka should be able to do this automatically.

[TimWhiting]

I will note that you do need to increase the stack space using ulimit. Maybe it is something that Koka could better document and warn users about. And maybe figure out a better way to use stack space. (Though for the majority of the time, it has no trouble - except for with ctl effects)

Also I compile with -O2 for optimizations.

[TimWhiting]

Here are the necessary changes to your handlers from the gist:

val reverse = handler {
  fun ap0(n) -> {
    Prop(op0(n), ref(c(0.0)))
  }
// No changes to the other two
  ...
}

val evaluate = handler {
  fun ap0(n) -> match(n) {Const(i) -> i}
  fun ap1(u,x: float64) -> match(u) {
    Negate -> ~x
    Sin -> sin(x)
    Cos -> cos(x)
    Exp -> exp(x)
  }
  fun ap2(b,x:float64,y: float64) -> match(b) {
    Plus -> x + y
    Subtract -> x - y
    Times -> x * y
    Divide -> x / y
  }
}

[TimWhiting]

I'm curious how the equivalent frank program performs on the same machine. Would be interesting comparison to see.