【Day 29 】2023-03-14 - 997. 找到小镇的法官

[azl397985856]

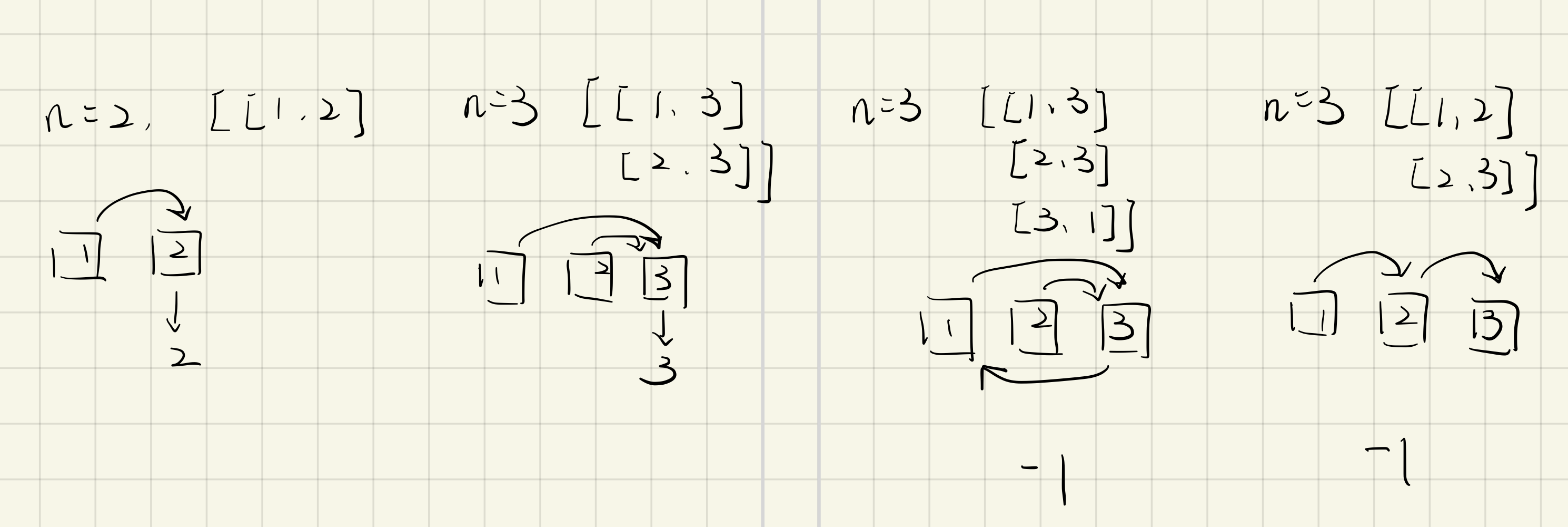
997. 找到小镇的法官

入选理由

暂无

题目地址

https://leetcode-cn.com/problems/find-the-town-judge/

前置知识

• 图

  题目描述

  
  在一个小镇里，按从 1 到 n 为 n 个人进行编号。传言称，这些人中有一个是小镇上的秘密法官。

如果小镇的法官真的存在，那么：

小镇的法官不相信任何人。 每个人（除了小镇法官外）都信任小镇的法官。 只有一个人同时满足条件 1 和条件 2 。

给定数组 trust，该数组由信任对 trust[i] = [a, b] 组成，表示编号为 a 的人信任编号为 b 的人。

如果小镇存在秘密法官并且可以确定他的身份，请返回该法官的编号。否则，返回 -1。

 

示例 1：

输入：n = 2, trust = [[1,2]] 输出：2

示例 2：

输入：n = 3, trust = [[1,3],[2,3]] 输出：3

示例 3：

输入：n = 3, trust = [[1,3],[2,3],[3,1]] 输出：-1

示例 4：

输入：n = 3, trust = [[1,2],[2,3]] 输出：-1

示例 5：

输入：n = 4, trust = [[1,3],[1,4],[2,3],[2,4],[4,3]] 输出：3

 

提示：

1 <= n <= 1000 0 <= trust.length <= 104 trust[i].length == 2 trust[i] 互不相同 trust[i][0] != trust[i][1] 1 <= trust[i][0], trust[i][1] <= n

[Yufanzh]

based on the requirement in the question,\n the judge should have outdegree of 0 and indegree of n-1.

class Solution:
    def findJudge(self, n: int, trust: List[List[int]]) -> int:
        # topologic sort
        graph = collections.defaultdict(list)
        outdegree = collections.defaultdict(int)
        for a, b in trust:
            graph[b].append(a)
            outdegree[a] += 1
        for i in range(1, n+1):
            if outdegree[i] == 0 and len(graph[i]) == n-1:
                return i
        return -1

[JiangyanLiNEU]

• dictionary
• T = O(N)
• S = O(N)

  class Solution:
  def findJudge(self, n: int, trust: List[List[int]]) -> int:
      aTrustb = {}
      bisTrusteda = {}
      for i in range(1, n+1):
          aTrustb[i] = set()
          bisTrusteda[i] = set()
      for a, b in trust:
          aTrustb[a].add(b)
          bisTrusteda[b].add(a)
      for key, value in bisTrusteda.items():
          if len(value) == n-1 and len(aTrustb[key]) == 0:
              return key
      return -1

[snmyj]

class Solution {
public:
    int findJudge(int n, vector<vector<int>>& trust) {
            unordered_map<int,int> hashs,hashs_judge;
            vector<int> res;
            if(trust.size()==0){ 
                if(n==1){ 
                    return 1;
                }
                return -1;
            }
            for(int i=0;i<trust.size();i++){
                hashs[trust[i][0]]++;
                hashs_judge[trust[i][1]]++;
            }
            for(auto x:hashs){

                    res.push_back(x.first);

            }
            sort(res.begin(),res.end());
            for(int i=0;i<res.size();i++){

                if(res[i]!=i+1) {
                    if(hashs_judge[i+1]==n-1)
                    return i+1;
                    else return -1;
                }
                if(i==res.size()-1&&!hashs.count(n)) {
                      if(hashs_judge[n]==n-1) return n;
                      else return -1;
                    }
            }
            return -1;
    }
};

[jmaStella]

思路

trust : edges from vertex a to vertex b Build a graph based on trust. Count the number of in-edge and out-edge if in-edge = n-1 and out-edge =0, it is the judge

代码

public int findJudge(int n, int[][] trust) {
        int[][] count = new int[n+1][n+1];

        for(int i=0; i<trust.length; i++){
            int a = trust[i][0];
            int b = trust[i][1];

            count[b][1]++;
            count[a][0]++;

        }

        for(int i=1; i<count.length; i++){
            if(count[i][0] == 0 && count[i][1] == n-1){
                return i;
            }
        }
        return -1;
    }

复杂度

时间O(E) E is the length of trust 空间O(N) N is the number of vertex(people)

[NorthSeacoder]

/**
 * @param {number} n
 * @param {number[][]} trust
 * @return {number}
 */
var findJudge = function(n, trust) {
    //找到一个有 n-1 个入度,0 个出度的节点
    //入度
    const to = new Array(n + 1).fill(0);
    //出度
    const from = new Array(n + 1).fill(0);
    for (let [a, b] of trust) {
        from[a]++;
        to[b]++;
    }
    for (let i = 1; i <= n; i++) {
        if ((from[i] === 0 && to[i] === n - 1)) return i;
    }
    return -1;
};

• TC:O(trust.length+n)
• SC:O(n)

[954545647]

// 最好还是分开两个数组更加直观一点
// 可以直接统计入度和出度的差，因为我们要找的是入度和出度差为 n -1 的点。这样可以将两个数组降低为一个数组，不过复杂度是一样的。
var findJudge = function (n, trust) {
  const count = new Array(n + 1).fill(0);
  for (const edge of trust) {
    const x = edge[0];
    const y = edge[1];
    count[y]++;
    count[x]--;
  }
  console.log(count)
  for (let i = 1; i <= n; ++i) {
    if (count[i] === n - 1) {
      return i;
    }
  }
  return -1;
};

[tzuikuo]

思路

法官就是被n-1个人信任，信任0个人 用两个map，记录每个人信任几个人和被几个人信任

代码

class Solution {
public:
    int findJudge(int n, vector<vector<int>>& trust) {
        map<int,int> trustcnt,trustedcnt;
        int m=trust.size();
        for(int i=0;i<m;i++){
            trustcnt[trust[i][0]-1]++;
            trustedcnt[trust[i][1]-1]++;
        }
        for(int i=0;i<n;i++){
            if(trustedcnt[i]==n-1&&trustcnt[i]==0) return i+1;
        }

        return -1;
    }
};

复杂度分析

• 时间：O(N)
• 空间：O(N) N=n

[joriscai]

思路

• 根据题意，法官不信任其他人，其他人都信任法官，故法官有n-1个人信任
• 遍历每个人的信任情况，统计每个人的被信任值，当信任值等于n-1时，则此人为法官

代码

javascript

/*
 * @lc app=leetcode.cn id=997 lang=javascript
 *
 * [997] 找到小镇的法官
 */

// @lc code=start
/**
 * @param {number} n
 * @param {number[][]} trust
 * @return {number}
 */
var findJudge = function(n, trust) {
  const counts = new Array(n + 1).fill(0)

  // 计算信任值
  // 被信任就是流入，信任别人就是流出
  for (const [i, j] of trust) {
    counts[i] -= 1
    counts[j] += 1
  }

  for (let i = 1; i < counts.length; i++) {
    if (counts[i] === (n - 1)) {
      return i
    }
  }

  return -1
};
// @lc code=end

复杂度分析

• 时间复杂度：O(n)，遍历一次信任数组，最后再遍历计数的数组，耗时为2n，即O(n)
• 空间复杂度：O(n)，需要存放每个人的信任值

[duke-github]

思路

图 计算每个节点的入度 如果有指向其他节点的 则直接-n代表这个人不是法官

复杂度

时间复杂度O（n ）空间复杂度O（n）

代码

    public static int findJudge(int n, int[][] trust) {
        int[] ans = new int[n];
        for (int[] temp : trust) {
            ans[temp[1] - 1] += 1;
            ans[temp[0] - 1] -= n;
        }
        for (int i = 0; i < n; i++) {
            if (ans[i] == n - 1) {
                return i + 1;
            }
        }
        return -1;
    }

[airwalkers]

\\ 思路，统计出入度

class Solution {
    public int findJudge(int n, int[][] trust) {
        int[] in = new int[n + 1];
        int[] out = new int[n + 1];
        for (int[] t: trust) {
            in[t[1]]++;
            out[t[0]]++;
        }
        for (int i = 1; i <= n; i++) {
            if (in[i] == n - 1 && out[i] == 0) {
                return i;
            }
        }
        return -1;
    }
}

[kofzhang]

思路

用一个列表存放每个人被信任的次数 如果这个人信任别人，把被信任次数变为-1 最后找到最大的被信任次数。如果等于n-1，返回这个人的位置

复杂度

时间复杂度：O(n) 空间复杂度：O(n)

代码

class Solution:
    def findJudge(self, n: int, trust: List[List[int]]) -> int:
        if not trust and n==1:
            return 1
        faguan = [0]*(n+1)
        for a,b in trust:  
            faguan[b]+=1  
            faguan[a]=-1
        res = max(faguan)
        if res == n-1:
            return faguan.index(res)
        return -1

[kofzhang]

思路

用一个列表存放每个人被信任的次数 如果这个人信任别人，把被信任次数变为-1 最后找到最大的被信任次数。如果等于n-1，返回这个人的位置

复杂度

时间复杂度：O(n) 空间复杂度：O(n)

代码

class Solution:
    def findJudge(self, n: int, trust: List[List[int]]) -> int:
        if not trust and n==1:
            return 1
        faguan = [0]*(n+1)
        for a,b in trust:  
            faguan[b]+=1  
            faguan[a]=-1
        res = max(faguan)
        if res == n-1:
            return faguan.index(res)
        return -1

[zpbc007]

思路

被人相信 value + 1，相信别人 value - 1，法官的 value 一定是 n - 1 注意, 编号从 1 开始

代码

export function findJudge(n: number, trust: number[][]): number {
    // 编号从 1 开始
    const trustValue: number[] = new Array(n + 1).fill(0)

    for (const [a, b] of trust) {
        // 相信了别人
        trustValue[a]--
        // 被别人相信
        trustValue[b]++
    }

    return trustValue.findIndex((value, index) => index !== 0 && value === n - 1)
}

复杂度

• 时间复杂度：O(n + m) m 为 trust 长度，trust 和 trustValue 都需要遍历一遍
• 空间复杂度：O(n)

[FlipN9]

class Solution {
    public int findJudge(int N, int[][] trust) {
        if (trust.length < N - 1) 
            return -1;

        int[] trustScores = new int[N + 1]; // 初始信用分都为 0, 包括法官对自己

        for (int[] t : trust) {
            trustScores[t[1]]++;
            trustScores[t[0]]--;
        }

        for (int i = 1; i <= N; i++) {
            if (trustScores[i] == N - 1)
                return i;
        }
        return -1;
    }
}

[linlizzz]

思路

1. 初始化一个长度为n的列表

2. 遍历trust，出现在trust[i][0]位置上对应的列表位置-1的元素置-1（信任别人），出现在trust[i][1]位置上对应的列表位置-1的元素若不为-1（信任过别人）则置+1（被别人信任）

3. 查找列表中是否有元素值为n-1，若有返回其下标（存在法官），否则返回-1（不存在法官）

代码

class Solution:
    def findJudge(self, n: int, trust: List[List[int]]) -> int:
        judge = [0]*n
        for i, j in trust:
            judge[i-1] = -1
            if judge[j-1] != -1:
                judge[j-1] += 1
        if n-1 in judge:
            return judge.index(n-1)+1
        else:
            return -1

复杂度分析

T(n) = O(len(trust))

S(n) = O(n)

[zol013]

class Solution:
    def findJudge(self, n: int, trust: List[List[int]]) -> int:
        indegree = [0] * n
        outdegree = [0] * n
        for relation in trust:
            indegree[relation[1] - 1] += 1
            outdegree[relation[0] - 1] += 1

        for i in range(n):
            if indegree[i] == n - 1 and outdegree[i] == 0:
                return i + 1

        return -1

[Horace7]

var findJudge = function(n, trust) {
    const cnts = new Array(n + 1), out = new Array(n + 1)
    cnts.fill(0)
    out.fill(0)
    for(const t of trust){
        cnts[t[1]]++
        out[t[0]]++
    }
    for(let i = 1; i <= n; i++)
        if(out[i] == 0 && cnts[i] == n - 1)
            return i
    return -1
};

[Abby-xu]

class Solution:
    def findJudge(self, n: int, trust: List[List[int]]) -> int:
        trusts = [0] * (n+1)
        for (a, b) in trust:
            trusts[a] -= 1
            trusts[b] += 1

        for i in range(1, len(trusts)):
            if trusts[i] == n-1: return i
        return -1

[Fuku-L]

思路

n为图的节点，trust[i] 为图的有向边。 依题意，需要找到出度为0，入度为 n-1 的节点。

1. 遍历trust数组，使用两个一维数组 in 和 out 统计节点的入度和出度。
2. 遍历 n，找到符合题意的节点下标返回，否则返回 -1.

代码

class Solution {
    public int findJudge(int n, int[][] trust) {
        int[] in = new int[n];
        int[] out = new int[n];
        for (int[] node : trust) {
            out[node[0]-1]++;
            in[node[1]-1]++;
        }
        for (int i = 0; i < n; i++) {
            if (out[i] == 0 && in[i] == (n-1)){
                return i+1;
            }
        }
        return -1;
    }
}

复杂度分析

• 时间复杂度：O(N+M)，其中,N 为小镇人数， M 为trust数组长度。
• 空间复杂度：O(N)，需要用两个 N 空间统计出度和入度。

[aoxiangw]

class Solution:
    def findJudge(self, n: int, trust: List[List[int]]) -> int:
        count = [0] * (n + 1)
        for a, b in trust:
            count[a] -= 1
            count[b] += 1

        for i in range(1, n + 1):
            if count[i] == n - 1:
                return i

        return -1

Time, Space: O(n)

[Zoeyzyzyzy]

class Solution {
    //Think of this situation as a directed graph,every node has indegree and out degree.
    //If curr node represents judge, we can know its indegree is n-1, outdegree is 0.
    //Time Complexity:O(m + n) m is length of trust, Space Complexity: O(n)
    public int findJudge(int n, int[][] trust) {
        int[] indegree = new int[n + 1];
        int[] outdegree = new int[n + 1];
        for (int i = 0; i < trust.length; i++) {
            outdegree[trust[i][0]]++;
            indegree[trust[i][1]]++;
        }
        for (int i = 1; i < n + 1; i++) {
            if (indegree[i] == n - 1 && outdegree[i] == 0) {
                return i;
            }
        }
        return -1;
    }

    //Optimize: use only one array to represent both indegree and outdegree.
    public int findJudge1(int n, int[][] trust) {
        int[] record = new int[n + 1];
        for (int[] cur : trust) {
            record[cur[0]]--;
            record[cur[1]]++;
            if (record[cur[1]] == n - 1)
                return cur[1];
        }
        return -1;
    }
}

[chanceyliu]

代码

function findJudge(n: number, trust: number[][]): number {
  const inDegrees = new Array(n + 1).fill(0);
  const outDegrees = new Array(n + 1).fill(0);
  for (const edge of trust) {
    const x = edge[0],
      y = edge[1];
    ++inDegrees[y];
    ++outDegrees[x];
  }
  for (let i = 1; i <= n; ++i) {
    if (inDegrees[i] === n - 1 && outDegrees[i] === 0) {
      return i;
    }
  }
  return -1;
}

复杂度分析

• 时间复杂度：O(n)
• 空间复杂度：O(n)

[FireHaoSky]

思路：

"""
按照讲义中的思路，先构建领接矩阵，然后将信任关系存入矩阵相应位置中，
然后统计当前节点的出度和入度，如果入度为n-1，出度为0，就是秘密法官，
这种情况下，存入时间复杂度O(m),统计时间复杂度O(n^2)
所以，领接矩阵改为两个单独列表，分别统计入度和出度，最后找到符合条件的下标。
"""

代码：python

class Solution:
    def findJudge(self, n: int, trust: List[List[int]]) -> int:
        in_trust = [0]*(n+1)
        out_trust = [0]*(n+1)
        for a,b in trust:
            in_trust[b] += 1
            out_trust[a] += 1

        for i in range(1,n+1):
            if in_trust[i] == n-1 and out_trust[i] == 0:
                return i
        return -1

复杂度分析

"""
时间复杂度：O(n+m),m为trust长度
空间复杂度：O(n)
"""

[csthaha]

/**
 * @param {number} n
 * @param {number[][]} trust
 * @return {number}
 */
var findJudge = function(n, trust) {
    const inDegrees = new Array(n + 1).fill(0);
    const outDegrees = new Array(n + 1).fill(0);
    for (const edge of trust) {
        const x = edge[0], y = edge[1];
        inDegrees[y]++;
        outDegrees[x]++;
    }
    for (let i = 1; i <= n; ++i) {
        if (inDegrees[i] === n - 1 && outDegrees[i] === 0) {
            return i;
        }
    }
    return -1;
};

[jiujingxukong]

解题思路

原来这个是图的题。我们可以将小镇中的人们之间的信任关系抽象为图的边，那么图中的点自然就是小镇中的人。这样问题就转化为求图中入度（或出度）为 n - 1 并且出度（或入度）为 0的点。
算法：

1. 初始化长度为 n 的两个数组 in_degree 和 out_degree，分别表示入度和出度信息，比如 in_degree[i] 表示顶点 i 的入度为 in_degress[i]。其中 n 为人数，也就是图中的顶点数。
2. 接下来根据题目给的 trust 关系建图。由于我们定义图的方式为a 信任 b 表示图中有一条从顶点 a 到顶点 b 的有向边。因此如果 a 信任 b，那么 a 的出度 + 1，b 的入度 +1 。
3. 最后遍历 in_degree 和 out_degree 找到满足 in_degree[i] 为 n - 1，并且 out_degress[i] 为 0 的点，返回即可。如果没有这样的点返回 -1。

解题代码

/**
 * @param {number} n
 * @param {number[][]} trust
 * @return {number}
 */
var findJudge = function (n, trust) {
  const count = new Array(n + 1).fill(0);
  for (const edge of trust) {
    const x = edge[0];
    const y = edge[1];
    count[y]++;
    count[x]--;
  }
  for (let i = 1; i < n + 1; i++) {
    if (count[i] === n - 1) {
      return i;
    }
  }
  return -1;
};

复杂度分析

时间复杂度：O（n） 空间复杂度：O（n）

[huifeng248]

class Solution:
    def findJudge(self, n: int, trust: List[List[int]]) -> int:
        dict_trust = {}
        has_trust = {}
        for i in range(1, n+1, 1):
            dict_trust[i] = []
            has_trust[i] = []
        for pair in trust:
            a, b = pair[0], pair[1]
            dict_trust[a].append(b)
            has_trust[b].append(a)

        for item in dict_trust.items():
            value = item[1]
            key = item[0]
            if len(value) == 0 and len(has_trust[key]) == n-1:
                return key

        return -1

# time complexity: O(Max(n, e)) n is the no of people, e is the no of trust pair.
# space complexity: O(n) n is the no of people

[aswrise]

class Solution:
    def findJudge(self, n, trust):
        rec = [[0, 0] for _ in range(n+1)]
        for s, e in trust:
            rec[e][0] += 1
            rec[s][1] += 1
        ans = -1
        for i in range(1, n+1):
            if rec[i][0] == n-1 and rec[i][1] == 0:
                if ans == -1:
                    ans = i
                else:
                    return -1
        return ans

[X1AOX1A]

0997. 找到小镇的法官

题目

小镇里有 n 个人，按从 1 到 n 的顺序编号。传言称，这些人中有一个暗地里是小镇法官。

如果小镇法官真的存在，那么：

小镇法官不会信任任何人。
每个人（除了小镇法官）都信任这位小镇法官。
只有一个人同时满足属性 1 和属性 2 。
给你一个数组 trust ，其中 trust[i] = [ai, bi] 表示编号为 ai 的人信任编号为 bi 的人。

如果小镇法官存在并且可以确定他的身份，请返回该法官的编号；否则，返回 -1 。

示例 1：
输入：n = 2, trust = [[1,2]]
输出：2

示例 2：
输入：n = 3, trust = [[1,3],[2,3]]
输出：3

示例 3：
输入：n = 3, trust = [[1,3],[2,3],[3,1]]
输出：-1

思路1：哈希表

• 从题目可知，judge: 被所有人信任但不信任任何人
• 因此可以用哈希表保存潜在的 judge，
  • 若其相信其他人，则不是 judge
  • 最终如果被其他所有人信任，则是 judge

代码1

class Solution:
    def findJudge(self, n: int, trust: List[List[int]]) -> int:
        # judge: 被所有人信任，但不信任任何人
        judges = {}
        for i in range(1, n+1):
            judges[i] = set()
        for [Out, In] in trust:
            # 小镇法官不会信任任何人
            if Out in judges: del judges[Out]
            if In in judges: judges[In].add(Out)
        if not judges: return -1
        # 只有一个人同时满足属性 1 和属性 2 
        judge = list(judges.keys())[0]
        supporters = list(judges.values())[0]        
        # 每个人（除了小镇法官）都信任这位小镇法官
        if supporters == set(range(1, n+1))-set([judge]): return judge
        else: return -1

• 时间复杂度：O(N)
• 空间复杂度：O(N)

思路2：图

• 将小镇的人抽象为图的点，信任关系抽象为边
• 法官：被其他所有人信任，即入度为 n-1

代码2

class Solution:
    def findJudge(self, n: int, trust: List[List[int]]) -> int:
        count = [0]*n
        for [Out, In] in trust:
            count[Out-1] -= 1
            count[In-1] += 1
        for i in range(n):
            if count[i]==n-1: return i+1
        return -1

• 时间复杂度：O(N)
• 空间复杂度：O(N)

[chocolate-emperor]

//求入度为n-1，出度位0的点，题目中已知没有重边，可以变成求 入度 + 出度之和为n-1的点。入度是正，出度是负。
class Solution {
public:
    int trusted[1000+5];
    int findJudge(int n, vector<vector<int>>& trust) {

        for(int i = 1; i <= n; i++){
            trusted[i] = 0;
        }

        for(auto person:trust){
            trusted[person[0]] -= 1;
            trusted[person[1]] += 1;
        }

        int town_judge = -1;
        for(int i = 1; i <= n; i++){
            if(trusted[i] == n-1)     town_judge = i;
        }
        return town_judge;
    }
};

[harperz24]

class Solution:
    def findJudge(self, n: int, trust: List[List[int]]) -> int:
        if len(trust) < n - 1:
            return -1

        if len(trust) <= 1:
            return trust[0][1] if trust else 1

        scores = [0] * (n + 1)

        for a, b in trust:
            scores[a] -= 1
            scores[b] += 1

        for i, score in enumerate(scores):
            if score == n - 1:
                return i

        return -1

    # time: O(n)
    # space: O(n)

[bookyue]

TC: O(n)
SC: O(n)

    public int findJudge(int n, int[][] trust) {
        int[] degrees = new int[n + 1];

        for (int[] t : trust) {
            degrees[t[0]]--;
            degrees[t[1]]++;
        }

        for (int i = 1; i <= n; i++)
            if (degrees[i] == n - 1) return i;

        return -1;
    }

[Bochengwan]

思路

法官的入度为n-1，出度为0

代码

class Solution {
    public int findJudge(int n, int[][] trust) {
        int[] inDegrees = new int[n + 1];
        int[] outDegrees = new int[n + 1];
        for (int[] edge : trust) {
            int x = edge[0], y = edge[1];
            ++inDegrees[y];
            ++outDegrees[x];
        }
        for (int i = 1; i <= n; ++i) {
            if (inDegrees[i] == n - 1 && outDegrees[i] == 0) {
                return i;
            }
        }
        return -1;
    }
}

复杂度分析

• 时间复杂度：O(N+M)，其中 N 为人数，M为trust长度
• 空间复杂度：O(N)

[Meisgithub]

class Solution {
public:
    int findJudge(int n, vector<vector<int>>& trust) {
        if (n == 1)
        {
            return 1;
        }
        unordered_map<int, pair<int, int>> mp;
        for (const auto &v : trust)
        {
            mp[v[0]].first += 1;
            mp[v[1]].second += 1;
        }
        for (const auto &[key, value] : mp)
        {
            if (value.first == 0 && value.second == n - 1)
            {
                return key;
            }
        }
        return -1;
    }
};

[Hughlin07]

class Solution {

public int findJudge(int n, int[][] trust) {
    int[] arr = new int[n+1];
    for(int [] tmp : trust){
        arr[tmp[0]]--;
        arr[tmp[1]]++;
    }

    for(int i = 1; i < n+1; i++){
        if(arr[i] == n-1){
            return i;
        }
    }
    return -1;
}

}

Time: O(n)

Space: O(n)

[JasonQiu]

• Find the node with n - 1 indegree and 0 outdegree

  class Solution:
  def findJudge(self, n: int, trust: List[List[int]]) -> int:
      out_d = defaultdict(int)
      in_d = defaultdict(int)
      for i in range(len(trust)):
          out_d[trust[i][0]] += 1
          in_d[trust[i][1]] += 1
      for i in range(1, n + 1):
          if out_d[i] == 0 and in_d[i] == n - 1:
              return i
      return -1

  Time: O(E) Space: O(n)

[RestlessBreeze]

code

class Solution {
public:
    int findJudge(int n, vector<vector<int>>& trust) {
        vector<int> indegree(n + 1);
        vector<int> outdegree(n + 1);

        for (int i = 0; i < trust.size(); i++)
        {
            outdegree[trust[i][0]]++;
            indegree[trust[i][1]]++;
        }

        int ans = 0;
        int flag = -1;
        for (int i = 1; i <= n; i++)
        {
            if (indegree[i] == n - 1 && outdegree[i] == 0)
            {
                ans++;
                flag = i;
            }

        }

        return ans == 1 ? flag : -1;
    }
};

[wangqianqian202301]

思路

用一个数组进行记录

代码

class Solution:
    def findJudge(self, n: int, trust: List[List[int]]) -> int:
        if len(trust) == 0:
            if n == 1:
                return 1
            else:
                return -1
        arr = [0 for i in range(10000)]
        for p in trust:
            a, b = p
            arr[a] = -1
            if arr[b] >= 0:
                arr[b] = arr[b] + 1
        for i, c in enumerate(arr):
            if c == n - 1:
                return i
        return -1

复杂度

O(n) O(n)

[xiaoq777]

class Solution {
    public int findJudge(int n, int[][] trust) {
        int[] in = new int[n];
        int[] out = new int[n];
        for (int[] t: trust) {
            in[t[1] - 1]++;
            out[t[0] - 1]++;
        }
        for (int i = 0; i < n; i++) {
            if (in[i] == n - 1 && out[i] == 0) {
                return i + 1;
            }
        }
        return -1;
    }
}

[GuitarYs]

··· python class Solution { public int findJudge(int n, int[][] trust) { int[] in = new int[n]; int[] out = new int[n]; for (int[] t: trust) { in[t[1] - 1]++; out[t[0] - 1]++; } for (int i = 0; i < n; i++) { if (in[i] == n - 1 && out[i] == 0) { return i + 1; } } return -1; } } ···

[yingchehu]

思路

找出 in degree = N-1， out degree = 0 的點

Code

class Solution:
    def findJudge(self, n: int, trust: List[List[int]]) -> int:
        in_degree = collections.defaultdict(int)
        out_degree = collections.defaultdict(int)
        for edge in trust:
            out_degree[edge[0]] += 1
            in_degree[edge[1]] += 1
        for i in range(1, n+1):
            if in_degree[i] == n - 1 and out_degree[i] == 0:
                return i
        return -1

複雜度

Time: O(N) Space: O(N)

[kangliqi1]

public int findJudge(int n, int[][] trust) { int[] in = new int[n]; int[] out = new int[n]; for (int[] node : trust) { out[node[0]-1]++; in[node[1]-1]++; } for (int i = 0; i < n; i++) { if (out[i] == 0 && in[i] == (n-1)){ return i+1; } } return -1; }

[wangzh0114]

思路

• 有向图中节点的入度和出度

  代码

  class Solution {
  public:
  int findJudge(int n, vector<vector<int>>& trust) {
      vector<int> inDegree(n + 1);
      vector<int> outDegree(n + 1);
  
      for(auto& edge : trust){
          int x = edge[0];
          int y = edge[1];
          inDegree[y]++;
          outDegree[x]++;
      }
      for(int i = 1; i <= n; i++){
          if(inDegree[i] == n - 1 && outDegree[i] == 0)
              return i;
      }
      return -1;
  }
  };

  ---

  复杂度分析

• TC:O(N)
• SC:O(N)

[franciszq]

思路

图的知识，被信任的人当作input，信任的人当作output

注意点

代码

class Solution {
public:
    int findJudge(int n, vector<vector<int>>& trust)
{
        if (trust.size() == 0 && n == 1) {
        return 1;
    }
    vector<int> in_array(n + 1);
    vector<int> out_array(n + 1);
    for (int i = 0; i < trust.size(); ++i) {
        int out_num = trust[i][0];
        int in_num = trust[i][1];
        in_array[in_num]++;
        out_array[out_num]++;
    }
    for (int i = 0; i <= n; ++i) {
        if (in_array[i] == n - 1 && out_array[i] == 0) {
            return i;
        }
    }
    return -1;
}
};

复杂度

时间复杂度：O(n)

空间复杂度：O(1)

[SoSo1105]

class Solution: def findJudge(self, n: int, trust: List[List[int]]) -> int: in_degree = collections.defaultdict(int) out_degree = collections.defaultdict(int) for edge in trust: out_degree[edge[0]] += 1 in_degree[edge[1]] += 1 for i in range(1, n+1): if in_degree[i] == n - 1 and out_degree[i] == 0: return i return -1

[KrabbeJing]

思路

出度为0，入度为n-1

代码

class Solution:
    def findJudge(self, n: int, trust: List[List[int]]) -> int:
        in_degree = [0] * (n + 1)
        out_degree = [0] * (n + 1)
        for a, b in trust:
            out_degree[a] += 1
            in_degree[b] += 1
        for i in range(1, n+1):
            if in_degree[i] == n-1 and out_degree[i] == 0:
                return i
        return -1 

[Lydia61]

997. 找到小镇的法官

思路

利用图的出入度，只有法官是入度 n-1 出度 0

代码

class Solution {
public:
    int findJudge(int n, vector<vector<int>>& trust) {
        vector<int> inDegrees(n + 1);
        vector<int> outDegrees(n + 1);
        for (auto& edge : trust) {
            int x = edge[0], y = edge[1];
            ++inDegrees[y];
            ++outDegrees[x];
        }
        for (int i = 1; i <= n; ++i) {
            if (inDegrees[i] == n - 1 && outDegrees[i] == 0) {
                return i;
            }
        }
        return -1;
    }
};

复杂度分析

• 时间复杂度：O(m+n)
• 空间复杂度：O(n)

[lp1506947671]

代码

class Solution:
     def findJudge(self, N, trust):
        count = [0] * (N + 1)
        for i, j in trust:
            count[i] -= 1
            count[j] += 1
        for i in range(1, N + 1):
            if count[i] == N - 1:
                return i
        return -1

复杂度分析

令 n 为数组长度。

• 时间复杂度：O(n)
• 空间复杂度：O(n)

[joemonkeylee]

思路

初始都是0 信任别人-1 被信任+1 所有 除了n-1 其他都是-1

代码

     public int FindJudge(int n, int[][] trust)
        {
            int[] other = new int[n + 1];

            for (int i = 0; i < trust.Length; i++)
            {
                //前面的人相信后面的人
                other[trust[i][0]]--;
                other[trust[i][1]]++;
            }

            int res = -1;
            for (int i = 1; i <= n; i++)
            {
                if (other[i] == (n - 1)) return i;
            }
            return res;
        }

复杂度分析

• 时间复杂度：O(n+trust.length)
• 空间复杂度：O(n)

[Jetery]

class Solution {
public:
    int a[1001];
    int findJudge(int n, vector<vector<int>>& trust) {
        for (vector<int> t : trust) {
            a[t[0]]--;
            a[t[1]]++;
        }
        for (int i = 1; i <= n; i++) {
            if (a[i] == n - 1) return i;
        }
        return -1;
    }
};

[AstrKing]

思路

图，也是经典题了，考虑到法官的出入度即可

代码

class Solution {
    public int findJudge(int n, int[][] trust) {
        int[] count = new int[n + 1];
        for (int[] edge : trust) {
            int x = edge[0];
            int y = edge[1];
            ++count[y];
            --count[x];
        }
        for (int i = 1; i < n + 1; i++) {
            if (count[i] == n - 1) {
                return i;
            }
        }
        return -1;
    }
}

复杂度分析

时间复杂度：O(n)

空间复杂度：O(n)