Idea
BFS
Code
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def verticalTraversal(self, root: Optional[TreeNode]) -> List[List[int]]:
seen = collections.defaultdict(list)
left, right = 0, 0
depth = 0
def bfs(root, row, col):
nonlocal left, right, depth
stack = collections.deque()
stack.append((root, 0, 0))
while stack:
l = len(stack)
depth+=1
for _ in range(l):
cur, row, col = stack.popleft()
left = min(left, col)
right = max(right, col)
seen[(col,row)].append(cur.val)
if cur.left:
stack.append((cur.left, row+1, col-1))
if cur.right:
stack.append((cur.right, row+1, col+1))
bfs(root, 0, 0)
ans = [[]for _ in range(right - left+1)]
for i in range(left, right+1):
for j in range(depth):
ans[i-left].extend(sorted(seen[(i,j)]))
return ansComplexity:
Time: O(N) Space: O(N)
987. 二叉树的垂序遍历
入选理由
暂无
题目地址
https://leetcode-cn.com/problems/vertical-order-traversal-of-a-binary-tree
前置知识
题目描述
对位于 (X, Y) 的每个结点而言,其左右子结点分别位于 (X-1, Y-1) 和 (X+1, Y-1)。
把一条垂线从 X = -infinity 移动到 X = +infinity ,每当该垂线与结点接触时,我们按从上到下的顺序报告结点的值(Y 坐标递减)。
如果两个结点位置相同,则首先报告的结点值较小。
按 X 坐标顺序返回非空报告的列表。每个报告都有一个结点值列表。
示例 1:
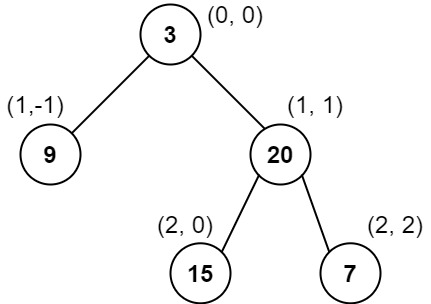
输入:[3,9,20,null,null,15,7] 输出:[[9],[3,15],[20],[7]] 解释: 在不丧失其普遍性的情况下,我们可以假设根结点位于 (0, 0): 然后,值为 9 的结点出现在 (-1, -1); 值为 3 和 15 的两个结点分别出现在 (0, 0) 和 (0, -2); 值为 20 的结点出现在 (1, -1); 值为 7 的结点出现在 (2, -2)。 示例 2:
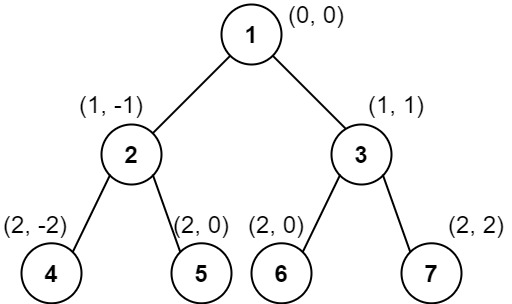
输入:[1,2,3,4,5,6,7] 输出:[[4],[2],[1,5,6],[3],[7]] 解释: 根据给定的方案,值为 5 和 6 的两个结点出现在同一位置。 然而,在报告 "[1,5,6]" 中,结点值 5 排在前面,因为 5 小于 6。
提示:
树的结点数介于 1 和 1000 之间。 每个结点值介于 0 和 1000 之间。