Thoughts Treat each point as the mid point, and calculate the distance between current point with all other points. Mapping the distance and the counts. Then traverse the keySet of map to get the total count of different pairs(EACH TIME WE SELECT TWO, so it's A(N, 2) = n * (n - 1))
Code
class Solution {
public int numberOfBoomerangs(int[][] points) {
int n = points.length;
int ans = 0;
for (int i = 0; i < n; i++) {
Map<Integer, Integer> map = new HashMap<>();
for (int j = 0; j < n; j++) {
if (i == j) continue;
int x = points[i][0] - points[j][0];
int y = points[i][1] - points[j][1];
int dist = x * x + y * y;
map.put(dist, map.getOrDefault(dist, 0) + 1);
}
for (int dis: map.keySet()) {
int count = map.get(dis);
ans += count * (count - 1);
}
}
return ans;
}
}Complexity Time: O(n ^ 2) Space: O(n)
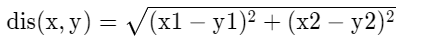 思路:
采用哈希表的方式存储,欧式算法的结果。过程如下
思路:
采用哈希表的方式存储,欧式算法的结果。过程如下
447. 回旋镖的数量
入选理由
暂无
题目地址
https://leetcode-cn.com/problems/number-of-boomerangs/
前置知识
题目描述
找到所有回旋镖的数量。你可以假设 n 最大为 500,所有点的坐标在闭区间 [-10000, 10000] 中。
示例:
输入: [[0,0],[1,0],[2,0]]
输出: 2
解释: 两个回旋镖为 [[1,0],[0,0],[2,0]] 和 [[1,0],[2,0],[0,0]]