I haven't done any formal tests (anyone care to instruct how to?) but here is a quick test against the yin implementation of #1063 - pyin was very similar, so I didn't include it separately:
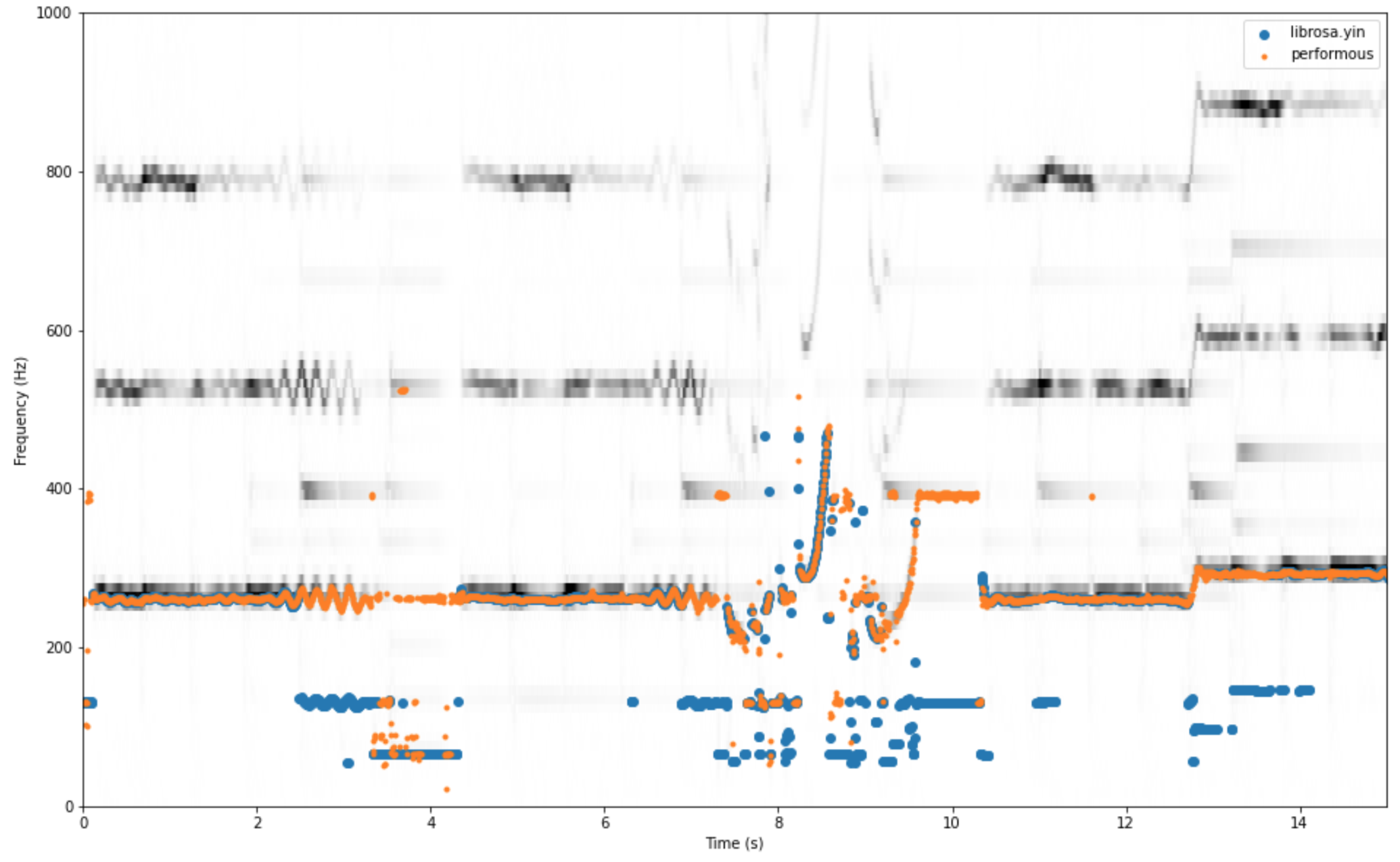
The audio file contains singing (with vibrato clearly seen on its fundamental and harmonics), and quieter piano sounds that are completely solid.
Hello,
I arrived to librosa while looking for libraries that could host my pitch detection algorithm. The algorithm is the third revision of the Performous vocal pitch detector, based on FFT reassignment method for finding precise frequencies, which are then combined into tones with most likely fundamental frequencies and their corresponding harmonics, and the third one I rewrote in Python/Numpy instead of C++ like the earlier ones. It can now detect one or few simultaneous tones with very little noise and accuracy better than 1 Hz, in real time (low latency, moderate CPU usage).
The question is, are you willing to take such non-standard algorithms into this library? FFT reassignment method could be one function and combination of harmonics another. Neither is specific to singing vocals, and as such could be used to detect any tonal signal. If that sounds good, I'll make a PR.
One consideration is that the algorithm needs to keep temporal state (overlapping FFTs and calculating phase differences). The current implementation is in class form so that such state can be preserved across incoming audio frames. If reduced to free function form like existing librosa algorithms, this cannot work in real time. If preferred, I could still restructure the algorithm into plain functions.