How to obtain the correct corr dim for Lorenz attractor.

[ricardofrantz]

Hi,

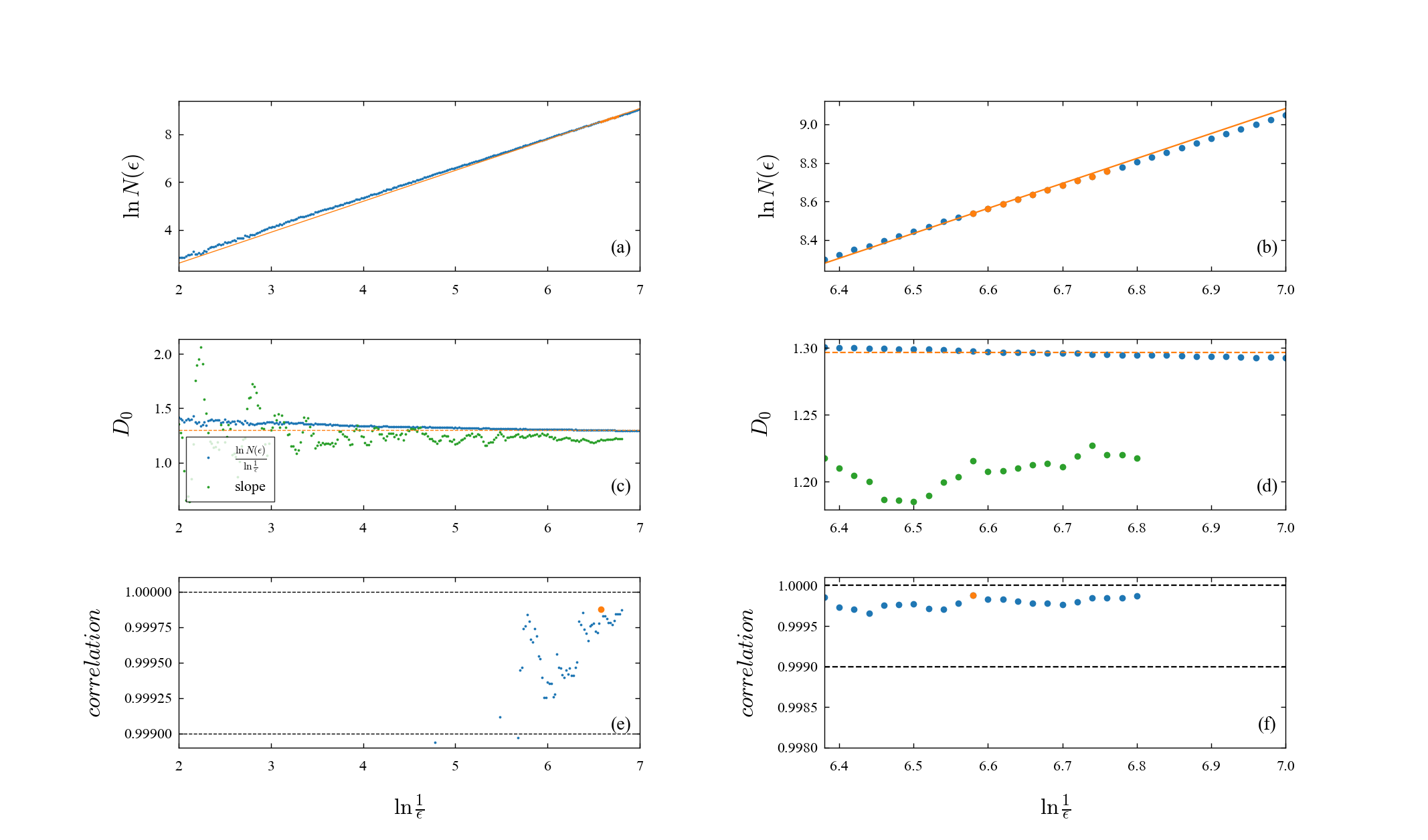
I'd like to extend my gratitude for developing such a library. I've chosen to raise a topic in the issues section, anticipating that others may also find it relevant. I aim to utilize your package to calculate the correlation dimension of various dynamical systems. However, to have confidence in the outcomes, I need to be able to replicate the commonly referenced dimension value of d=2.05±0.01 for the Lorenz attractor with (sigma, rho, beta)=(10, 28, 8/3). Ideally, my goal is to generate a figure akin to the one attached. I find it perplexing that most packages, despite claims of this capability, seldom demonstrate this value in their documentation or examples. Could you provide any guidance or examples that successfully achieve this benchmark?

Thanks for your time, Ricardo

[ricardofrantz]

So far I managed to obtain:

from hundun.exploration import calc_dimension_correlation, calc_dimension_information, calc_dimension_capacity
from hundun.equations import Lorenz
u_seq = Lorenz.get_u_seq(20000)

D_0 = calc_dimension_capacity(u_seq, depsilon=0.02, base=7, loop=250, min_correlation=0.999, scale_down=True, batch_ave=10, plot=True, path_save_plot='./capacity.png')
print('D_0=',D_0) # capacity dimension
D_1 = calc_dimension_information(u_seq, depsilon=0.02, base=7, loop=250, min_correlation=0.999, scale_down=True, batch_ave=10, plot=True, path_save_plot='./information.png')
print('D_1=',D_1) # information dimension
D_2 = calc_dimension_correlation(u_seq, depsilon=0.02, base=7, loop=250, min_correlation=0.999, scale_down=True, batch_ave=10, plot=True, path_save_plot='./correlation.png')
print('D_2=',D_2) # correlation dimension

D_0= 1.9669881090760062
D_1= 1.9044696394480827
D_2= 2.0757415161772044

Questions: Is the value of 20000 the final time or the number of steps? How do we know the time series is long enough? How can we know that the value we obtain is realistic when I have no reference value?

Thanks for your time, Ricardo

[llbxg]

Thank you for opening this issue! I would like to answer a few questions :bowtie:

Is the value of 20000 the final time or the number of steps?

This library treats equations as a class called Differential . When solving Differential, RK4 is used by default [^1].

So, here the 20000 refers to the number of steps.

The function get_u_seq in Lorenz obtains the time series by two steps. First, it generates a random number near the origin ^2, from which it calculates 5000 steps and puts the trajectory on the attractor ^3. Next, assuming that the trajectory is on the attractor, a time series of 20000 steps is generated.

How do we know the time series is long enough?

Each function has certain evaluation criteria.

For example, in calc_dimension_capacity, a condition is that the value of the correlation coefficient within the batch interval must be 0.999 or higher. If this condition is not met, it may indicate that there is an insufficient number of data points, or the data sampling interval is too large, leading to a lack of information.

)

Detailed certain evaluation criteria on wiki [^4][^5].

How can we know that the value we obtain is realistic when I have no reference value?

This is a very difficult question :pensive:

Personally, I believe that for unknown time series, it is good to check the graph and certain evaluation criteria their appropriateness. For example, if the amount of information in the time series data is obviously insufficient, it can be understood instantly.

It is very difficult to establish appropriate batch sizes, thresholds, etc. for time series. Therefore, we can only plot the actual measured data and determine that the results seem to be correct.

I currently have no ideas other than empirical judgments, but if you have any ideas, please share them with us.

About Others

To obtain better results, the data sampling interval is crucial [^6]. A certain level of detail is necessary, but if it's too fine, it requires a larger amount of data. This, in turn, leads to an increase in computation time [^7].

If the sampling interval is too short, it will not sufficiently cover the entire attractor.

If you have any more questions, please feel free to ask :wave:

[^1]: That is, use a fixed time step. The step size is set to h=0.01 by default.

[^5]: Unfortunately, the service we used to post the equations seems to have been terminated. It needs to be updated :construction_worker: [^6]: Sample: Lorenz.get_u_seq(200000, h=0.001) [^7]: Unfortunately, as this library is not optimized for computation, please be aware that it can be very time-consuming.

[ricardofrantz]

Thanks for taking the time to respond. I will run more tests and try to digest your suggestions!