Hi. For the future, you can directly add references (hyperlink) to pieces of code in github that will help assisting you. For instance https://github.com/loco-3d/sl1m/blob/64dca822a2fddddb8ed5fd089f67d494a836ea96/problem_definition.py#L33
Just to be clear you are currently looking that constraint files that have been defined for humanoid robots in an ad doc way used only for the biped robot. For the anymal files look here:
https://github.com/loco-3d/sl1m/blob/quadruped/stand_alone_scenarios/constraints_anymal.py
1) Given the surface normal and current root orientation, we compute the foot orientation matrix that corresponds to the foot being aligned on the surface. The z orientation of the foot is aligned with the one of the root orientation. Thus the kinematic constraints with respect to this foot will be expressed in this frame. Note that this only matters for the humanoid robot. For the Quadruped the contacts are considered to be 3D and this the surface orientation is not relevant for the kinematic constraints.
2) This function expresses the COM constraints in the frame of the contacting foot as a set of linear inequalities.
3) Suppose the COM x position, called cx, is constrained to be 1 meter away from the foot position px.
The constraint is written with 2 inequalities: (cx - px) <= 1 (cx - px) >= -1
The inequality constraints are valid for a foot position located a 0,0,0. if the position is different from the origin the constraints must be "translated" by the x position
Dear professor,
Currently, I am studying an example of bipedal (escaliers.py), because it is difficult to understand the quadruped example (flat_ground.py) directly.
I have some questions on the SL1M code
default_transform_from_posnormal(rotation[index], zero3, normals[LF])
genKinematicConstraints(left_foot_constraints,right_foot_constriants) I understood that the obtained inequality equation which represented as a OBJ file was written as a local frame of the foot.
surfacePointsToIneq(s, n, eqAsIneq)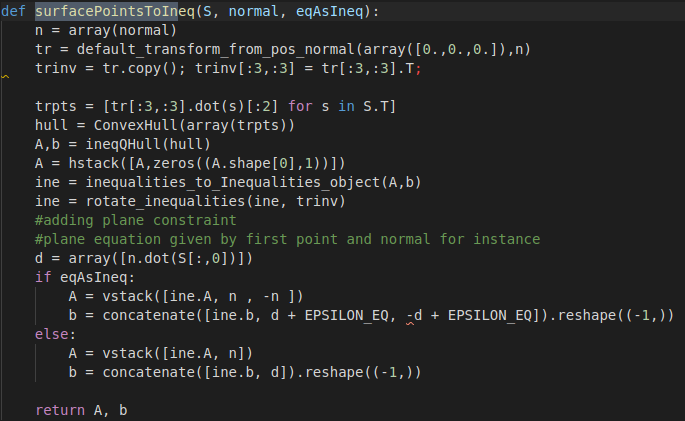
def MovingFootCOMConstraintInitPhase(pb, phaseDataT, A, b, startCol, endCol, startRow):