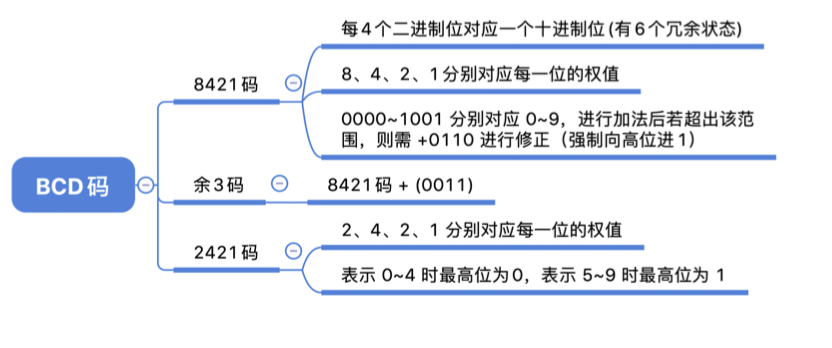
BCD码
BCD :Binary-Coded Decimal,用二进制编码的十进制
二进制:0,1 方便计算机处理
十进制:0,1,2,3,4,5,6,7,8,9 符合人类习惯
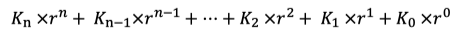 转换麻烦
转换麻烦
快速转换:一一对应
8421码的映射关系:

 手算方法
手算方法
 机算方法
机算方法
不在映射表里 8421码中 1010~1111 没有定义
+6 +0110进行修正
注:若相加结果在合法范围内,则无需修正。
余三码(无权码)

2421码:改变权值定义

总结
Closed loyio closed 3 years ago
BCD :Binary-Coded Decimal,用二进制编码的十进制
二进制:0,1 方便计算机处理
十进制:0,1,2,3,4,5,6,7,8,9 符合人类习惯
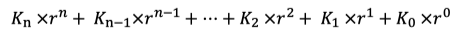 转换麻烦
转换麻烦
快速转换:一一对应
8421码的映射关系:

 手算方法
手算方法
 机算方法
机算方法
不在映射表里 8421码中 1010~1111 没有定义
+6 +0110进行修正
注:若相加结果在合法范围内,则无需修正。
余三码(无权码)

2421码:改变权值定义


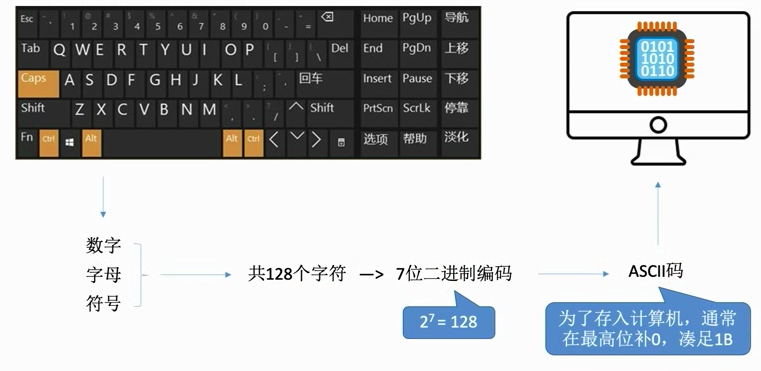
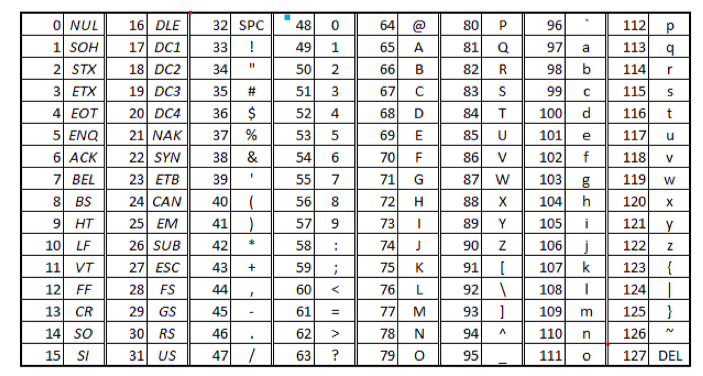
可印刷字符:32~126,其余为控制、通信字符
数字:48(0011 0000)~57(0011 1001)
大写字母:65(0100 0001)~90(0101 1010)
小写字母:97(0110 0001)~122(0111 1010)
GB 2312-80 : 汉字+各种符号共7445个
区位码:94个区,每区94个位置
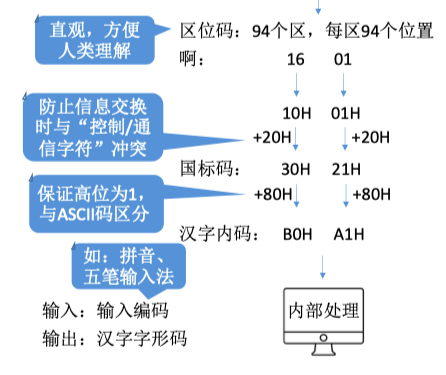
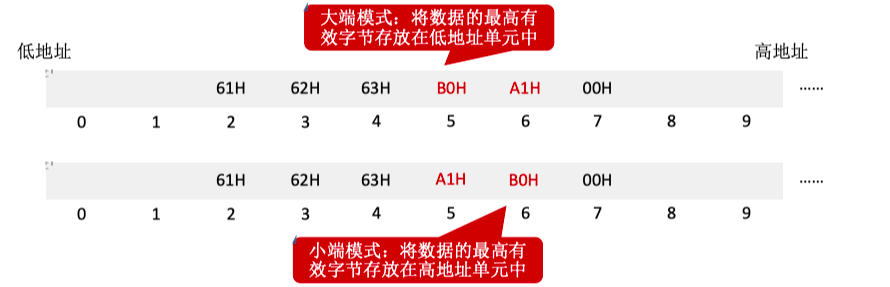
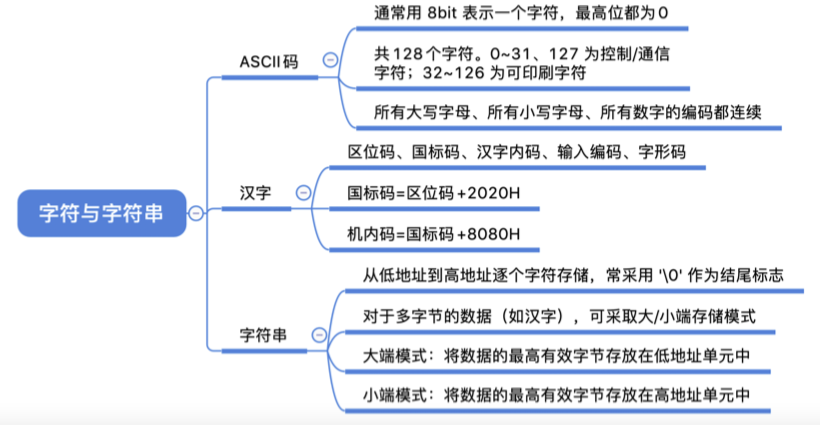
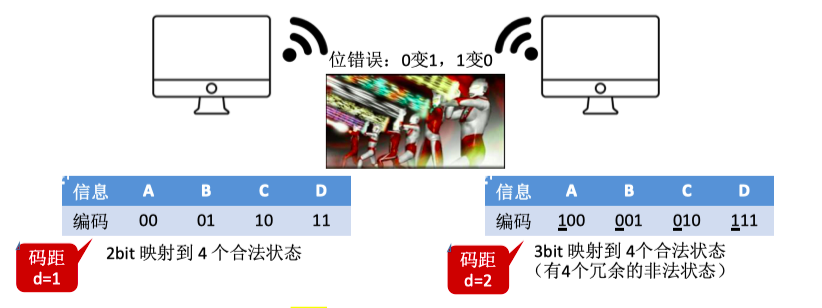
由若干位代码组成的一个字叫码字。
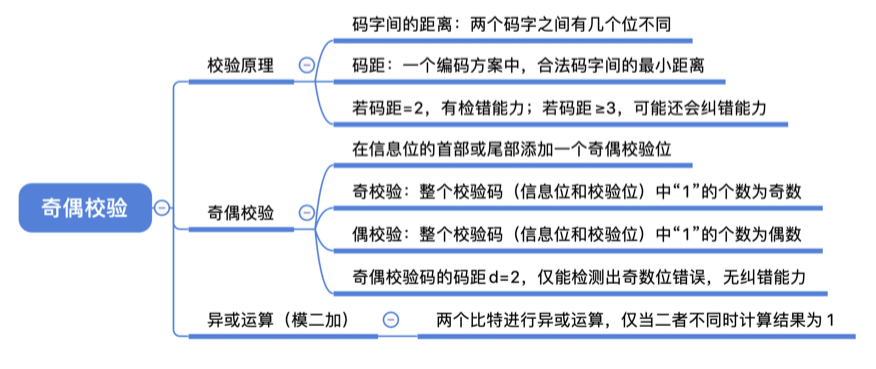
将两个码字逐位进行对比,具有不同的位的个数称为两个码字间的距离。 一种编码方案可能有若干个合法码字,各合法码字间的最小距离称为“码距”。
当d=1时,无检错能力;当d=2时,有检错能力;当d≥3时,若设计合理,可能具有检错、纠错能力
奇校验码:整个校验码(有效信息位和校验位)中“1”的个数为奇数。
偶校验码:整个校验码(有效信息位和校验位)中“1”的个数为偶数。
偶校验的硬件实现:各信息进行异或(模2加)运算,得到的结果即为偶校验位


奇校验码:整个校验码(有效信息位和校验位)中“1”的个数为奇数。
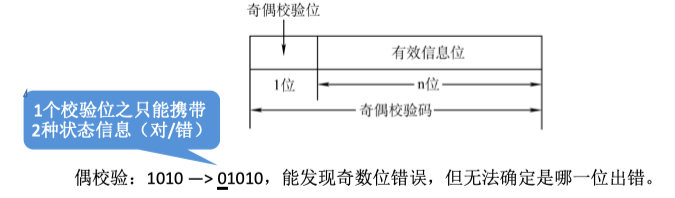
偶校验码:整个校验码(有效信息位和校验位)中“1”的个数为偶数。
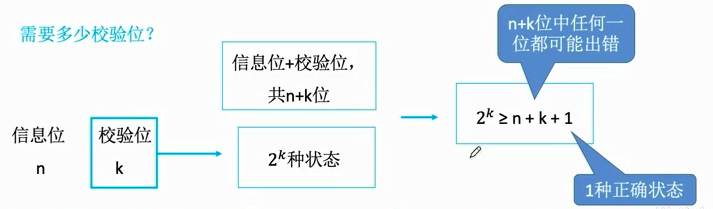
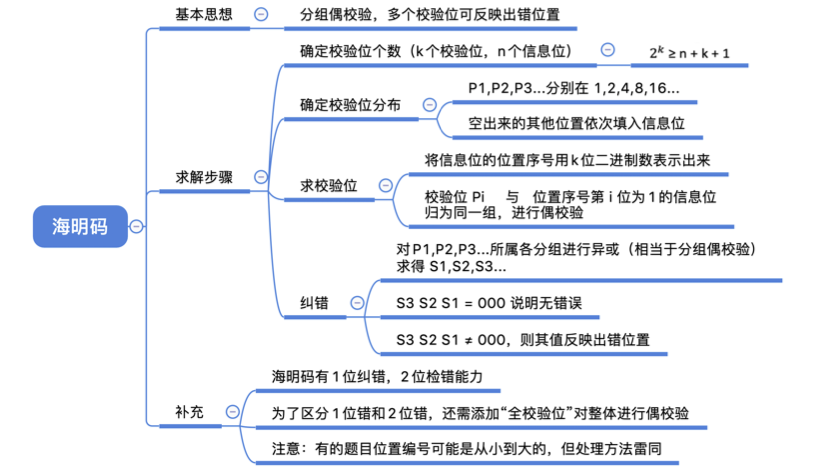
海明码设计思路:将信息位分组进行偶校验 —> 多个校验位—>多个校验位标注出错位置
多个校验位能携带多种状态信 息,(对/错,错在哪)

信息位:1010
1.确定海明码的位数: 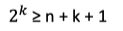
n=4—>k=3
设信息位D4 D3 D2 D1 (1010),共4位,校验位P3 P2 P1 , 共3位,对应的海明码为H7 H6 H5 H4 H3 H2 H1。
2.确定校验位的分布
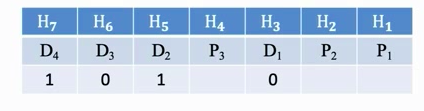
校验位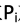 放在海明位号为
放在海明位号为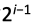 的位置上
的位置上
信息位按顺序放到其余位置
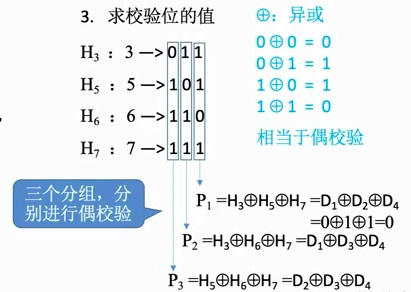
3.求检验位的值
4.纠错
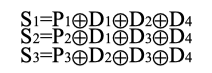
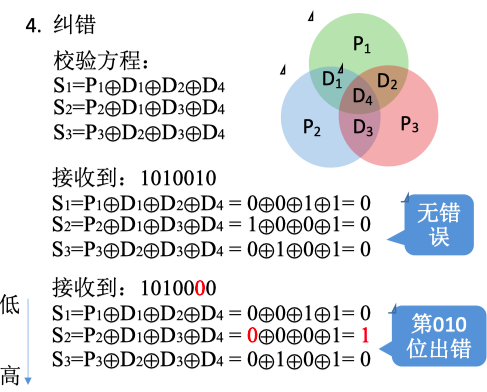
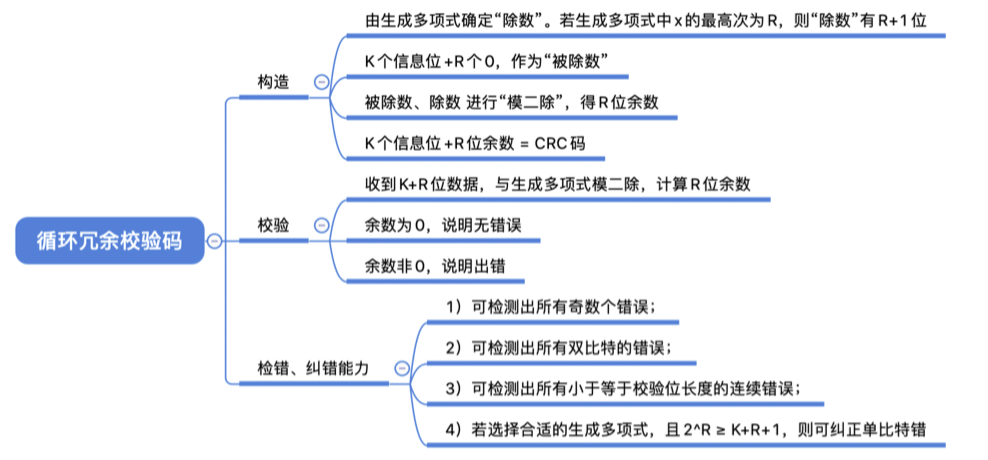
海明码的检错、纠错能力:
纠错能力——1位
检错能力——2位
无法区分到底是1 位错还是2位错

需加上“全校验位”,对整体进行偶校验
循环冗余校验(Cyclic Redundancy Check, CRC)
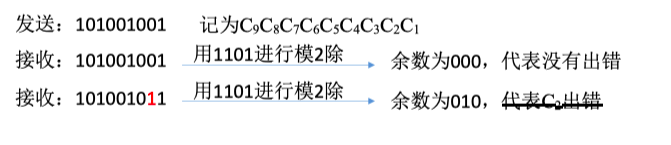
数据出错导致余数改变——检测到错误
循环冗余校验码的思想:
数据发送、接受方约定一个“除数”(二进制)
K个信息位+R个校验位 作为“被除数”,添加校验位后需保证除法的余数为0
收到数据后,进行除法检查余数是否为0
若余数非0说明出错,则进行重传或纠错

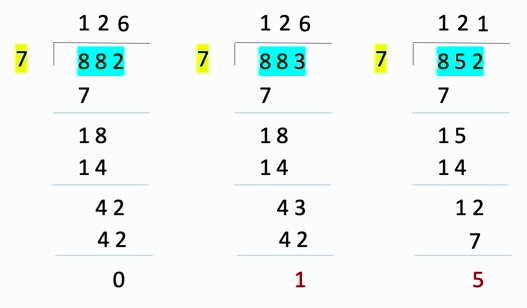
模2除法
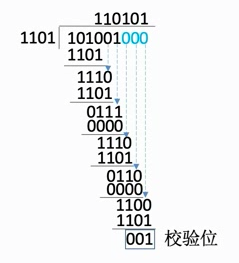
对应的CRC码: 101001 001
4.检错和纠错


进位计数制
最古老的计数方法
十进制计数法
古印度人发明的阿拉伯数字:0,1,2,3,4,5,6,7,8,9 符号反映权重
符号所在的位置也反映权重
推广:r进制计数法
基数:每个数码位所用到的不同符号的个数,r 进制的基数为 r
二进制:
任意进制→十进制
二进制←→八进制、十六进制
二进制→八进制
3位一组,毎组转换成对应的八进制符号
二进制→十六进制
4位一组,毎组转换成对应的十六进制符号
八进制→二进制
每位八进制对应的3位二进制
十六进制→二进制
每位十六进制对应的4位二进制
各种进制的常见书写方式
十进制→任意进制
真值和机器数
真值:符合人类习惯的数字
机器数:数字实际存到机器里的形式,正负号需要被“数字化”