See "Q: I failed to train the network, e.g., the training loss is large." at "Questions & Answers" at the webpage.
Note: net.outputs_modify() is renamed to net.apply_output_transform()
Closed wangcj05 closed 4 years ago
See "Q: I failed to train the network, e.g., the training loss is large." at "Questions & Answers" at the webpage.
Note: net.outputs_modify() is renamed to net.apply_output_transform()
I think you should normalize you PDE or apply network output transform, the scales of your parameters differ a lot.
@lululxvi @qizhang94 Thanks a lot for your answers. I have tried to scale the problem. Since the solution for this problem is between [300, 1000]. I have rescaled the problem by 100. In addition, I have also tried to use the loss_weight to rescale the weight. However, the problem does not converge. Do you have any suggestions?
The updated code is provided:
mport numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
import deepxde as dde
from scipy.interpolate import griddata
import matplotlib.gridspec as gridspec
from mpl_toolkits.mplot3d import axes3d
# geometry parameters
xdim = 200
ydim = 100
xmin = 0.0
ymin = 0.0
xmax = 0.04
ymax = 0.02
# input parameters
rho = 8000
cp = 500
k = 200
T0 = 300
Tinit = 1000
t0 = 0.0
te = 30.0
x_start = 0.0 # laser start position
# dnn parameters
num_hidden_layer = 3 # number of hidden layers for DNN
hidden_layer_size = 40 # size of each hidden layers
num_domain=1000 # number of training points within domain Tf: random points (spatio-temporal domain)
num_boundary=1000 # number of training boundary condition points on the geometry boundary: Tb
num_initial= 1000 # number of training initial condition points: Tb
num_test=None # number of testing points within domain: uniform generated
epochs=10000 # number of epochs for training
lr=0.001 # learning rate
def main():
def pde(x, T):
dT_x = tf.gradients(T, x)[0]
dT_x, dT_y, dT_t = dT_x[:,0:1], dT_x[:,1:2], dT_x[:,2:]
dT_xx = tf.gradients(dT_x, x)[0][:, 0:1]
dT_yy = tf.gradients(dT_y, x)[0][:, 1:2]
return rho*cp*dT_t - k*dT_xx - k*dT_yy
def boundary_x_l(x, on_boundary):
return on_boundary and np.isclose(x[0], xmin)
def boundary_x_r(x, on_boundary):
return on_boundary and np.isclose(x[0], xmax)
def boundary_y_b(x, on_boundary):
return on_boundary and np.isclose(x[1], ymin)
def boundary_y_u(x, on_boundary):
return on_boundary and np.isclose(x[1], ymax)
def func(x):
return np.ones((len(x),1), dtype=np.float32)*T0
def func_n(x):
return np.zeros((len(x),1), dtype=np.float32)
def func_init(x):
return np.ones((len(x),1), dtype=np.float32)*Tinit
geom = dde.geometry.Rectangle([0, 0], [xmax, ymax])
timedomain = dde.geometry.TimeDomain(t0, te)
geomtime = dde.geometry.GeometryXTime(geom, timedomain)
bc_x_l = dde.DirichletBC(geomtime, func, boundary_x_l)
bc_x_r = dde.DirichletBC(geomtime, func, boundary_x_r)
bc_y_b = dde.DirichletBC(geomtime, func, boundary_y_b)
bc_y_u = dde.NeumannBC(geomtime, func_n, boundary_y_u)
ic = dde.IC(geomtime, func_init, lambda _, on_initial: on_initial)
data = dde.data.TimePDE(
geomtime,
pde,
[bc_x_l, bc_x_r, bc_y_b, bc_y_u, ic],
num_domain=num_domain,
num_boundary=num_boundary,
num_initial=num_initial,
# train_distribution="uniform",
num_test=num_test
)
net = dde.maps.FNN([3] + [hidden_layer_size] * num_hidden_layer + [1], "tanh", "Glorot uniform")
# net.apply_output_transform(lambda x, y: y*1000)
net.apply_output_transform(lambda x, y: y*100)
model = dde.Model(data, net)
model.compile("adam", lr=lr, loss_weights=[1e-12, 1e-2, 1e-2, 1e-2, 1, 1e-3])
# model.compile("adam", lr=lr)
losshistory, train_state = model.train(epochs=epochs)
# model.compile("L-BFGS-B")
# losshistory, train_state = model.train()
dde.saveplot(losshistory, train_state, issave=False, isplot=False)
if __name__ == "__main__":
main()
Try to train for more iterations.
Try to train for more iterations.
@lululxvi, I have tried your suggestion, but the problem still does not converge (see the attached picture):

There are some problems of the scaling:
te first, e.g., 1T, which is easy for your problem, instead of using net.apply_output_transform.@lululxvi I Thanks for your quick response. have tried different orders, i.e. 100 and 1000 using the net.apply_output_transform, the problem still suffers the convergence issue. I will try your suggestions to rescale the geometry and T with small end of time.
Hello @wangcj05 ! I am trying to solve a similar problem. Did you achieve convergence?
@Huzaifg Unfortunately, I do not get the problem converged.
@wangcj05 I actually got this to work a while back but forgot to update here.
This is the equation I solved
 First, I normalized the equation
First, I normalized the equation
 And made some modifications to the boundary conditions
And made some modifications to the boundary conditions
 I also applied a output transform to ensure that the tempretures that the DNN was outputing were positive using
I also applied a output transform to ensure that the tempretures that the DNN was outputing were positive using
net.apply_output_transform(lambda x, y: abs(y))
Given below is the complete code
import deepxde as dde
import matplotlib.pyplot as plt
import numpy as np
from deepxde.backend import tf
# Some useful functions
t1 = 0
t2 = 1
end_time = 1
def pde(X,T):
dT_xx = dde.grad.hessian(T, X ,j=0)
dT_yy = dde.grad.hessian(T, X, j=1)
dT_t = dde.grad.jacobian(T, X, j=2)
# Dividing by rhoc to make it 1
rhoc = (3.8151 * 10**3) / (3.8151 * 10**3)
kap = (385 / (3.8151 * 10**3))
# no forcing function
return ((rhoc * dT_t) - (kap * (dT_xx + dT_yy)))
def r_boundary(X,on_boundary):
x,y,t = X
return on_boundary and np.isclose(x,1)
def l_boundary(X,on_boundary):
x,y,t = X
return on_boundary and np.isclose(x,0)
def up_boundary(X,on_boundary):
x,y,t = X
return on_boundary and np.isclose(y,1)
def down_boundary(X,on_boundary):
x,y,t = X
return on_boundary and np.isclose(y,0)
def boundary_initial(X, on_initial):
x,y,t = X
return on_initial and np.isclose(t, 0)
def init_func(X):
x = X[:, 0:1]
y = X[:, 1:2]
t = np.zeros((len(X),1))
for count,x_ in enumerate(x):
if x_ < 0.5:
t[count] = t1
else:
t[count] = t1 + (2) * (x_ - 0.5)
return t
def dir_func_l(X):
return t1 * np.ones((len(X),1))
def dir_func_r(X):
return t2 * np.ones((len(X),1))
def func_zero(X):
return np.zeros((len(X),1))
def hard(X, T):
x,y,t = x[:, 0:1], x[:, 1:2],x[:,2:3]
return (r - r_in) * y + T_star
num_domain = 30000
num_boundary = 8000
num_initial = 20000
layer_size = [3] + [60] * 5 + [1]
activation_func = "tanh"
initializer = "Glorot uniform"
lr = 1e-3
# Applying Loss weights as given below
# [PDE Loss, BC1 loss - Dirichlet Left , BC2 loss - Dirichlet Right, BC3 loss- Neumann up, BC4 loss - Neumann down, IC Loss]
loss_weights = [10, 1, 1, 1, 1, 10]
epochs = 10000
optimizer = "adam"
batch_size_ = 256
geom = dde.geometry.Rectangle(xmin=[0, 0], xmax=[1, 1])
timedomain = dde.geometry.TimeDomain(0, end_time)
geomtime = dde.geometry.GeometryXTime(geom, timedomain)
bc_l = dde.DirichletBC(geomtime, dir_func_l, l_boundary)
bc_r = dde.DirichletBC(geomtime, dir_func_r, r_boundary)
bc_up = dde.NeumannBC(geomtime, func_zero, up_boundary)
bc_low = dde.NeumannBC(geomtime, func_zero, down_boundary)
ic = dde.IC(geomtime, init_func, boundary_initial)
data = dde.data.TimePDE(
geomtime, pde, [bc_l, bc_r, bc_up, bc_low, ic], num_domain=num_domain, num_boundary=num_boundary, num_initial=num_initial)
net = dde.maps.FNN(layer_size, activation_func, initializer)
net.apply_output_transform(lambda x, y: abs(y))
## Uncomment below line to apply hard Dirichlet Boundary Conditions
# net.outputs_modify(lambda x, y: x[:,0:1]*t2 + x[:,0:1] * (1 - x[:,0:1]) * y)
model = dde.Model(data, net)
model.compile(optimizer, lr=lr,loss_weights=loss_weights)
# To save the best model every 1000 epochs
checker = dde.callbacks.ModelCheckpoint(
"model/model1.ckpt", save_better_only=True, period=1000
)
losshistory, trainstate = model.train(epochs=epochs,batch_size = batch_size_,callbacks = [checker])
model.compile("L-BFGS-B")
dde.optimizers.set_LBFGS_options(
maxcor=50,
)
losshistory, train_state = model.train(epochs = epochs, batch_size = batch_size_)
dde.saveplot(losshistory, trainstate, issave=True, isplot=True)The best results achieved,

 I also predicted the temperature for a paticular time frame using the code given below
I also predicted the temperature for a paticular time frame using the code given below
import matplotlib.animation as animation
from matplotlib.animation import FuncAnimation
ax = fig.add_subplot(111)
nelx = 100
nely = 100
timesteps = 101
x = np.linspace(0,1,nelx+1)
y = np.linspace(0,1,nely+1)
t = np.linspace(0,1,timesteps)
delta_t = t[1] - t[0]
xx,yy = np.meshgrid(x,y)
x_ = np.zeros(shape = ((nelx+1) * (nely+1),))
y_ = np.zeros(shape = ((nelx+1) * (nely+1),))
for c1,ycor in enumerate(y):
for c2,xcor in enumerate(x):
x_[c1*(nelx+1) + c2] = xcor
y_[c1*(nelx+1) + c2] = ycor
Ts = []
for time in t:
t_ = np.ones((nelx+1) * (nely+1),) * (time)
X = np.column_stack((x_,y_))
X = np.column_stack((X,t_))
T = model.predict(X)
T = T*30
T = T.reshape(T.shape[0],)
T = T.reshape(nelx+1,nely+1)
Ts.append(T)
def plotheatmap(T,time):
# Clear the current plot figure
plt.clf()
plt.title(f"Temperature at t = {time*delta_t} unit time")
plt.xlabel("x")
plt.ylabel("y")
plt.pcolor(xx, yy, T,cmap = 'RdBu_r')
plt.colorbar()
return plt
def animate(k):
plotheatmap(Ts[k], k)
anim = animation.FuncAnimation(plt.figure(), animate, interval=1, frames=len(t), repeat=False)
anim.save("trial1.gif")You can also find the gif converted to a mp4 file at the Gdrive link https://drive.google.com/file/d/1t_uWzJT6ks1uMT0EKChcw7b-HqPJGtzW/view?usp=sharing
Please do let me know if I could have done something better or some mistakes that you find, I am only starting out and would love to learn!
@Huzaifg Thank you for an excellent explanation and code upload. Works perfectly. Speaking as an IoT engineer this would have taken months to understand and problem solve. has given a much deeper understanding of practical uses for deepXDE.
thanks again.
Hey @MINE0126
Can you post your loss vs Epochs graph for the above result?
Hello, @Huzaifg Thank you for your answer. I have solved this question.Thank again. But I have a new problem https://github.com/lululxvi/deepxde/discussions/874. Hope you can help me, thank you.
Hi~ @MINE0126 Would you mind posting the correct code here? Thans in advance!
@Huzaifg Hi. I would like to know the parameters and region normalization about PDE. I see that the space-time regions in your model are all from 0 to 1, and divide rhoc and kap by 3.8E3. Is this related to the problem scaling described in the above discussion? I wanted to explore this aspect to see if it would help my model. Below are my PDE and space-time region codes. I hope you can give me some suggestions on normalization or scaling.
`a1=1.67e-4 a2=0.45 a3=5e-4 a4=0.45 def pde(x, u): p,s = u[:, 0:1], u[:, 1:2]
dp_xx = dde.grad.hessian(u, x, component=0, i=0, j=0)
dp_yy = dde.grad.hessian(u, x, component=0, i=1, j=1)
ds_t = dde.grad.jacobian(u, x, i=1, j=2)
f_o=a1*(dp_xx+dp_yy)-a2*ds_t
f_w=a3*(dp_xx+dp_yy)+a4*ds_t
return [f_o,f_w]geom = dde.geometry.Rectangle(xmin=[0,0], xmax=[5,5]) timedomain=dde.geometry.TimeDomain(0,30) geomtime=dde.geometry.GeometryXTime(geom,timedomain)`
Thanks!
Hello @123new-net , Yes, this was done to encounter the scaling problem as described above. I am unsure how you should go about scaling your problem, its been a while since I have solved a problem like this.
Hi~ @Huzaifg The initial function needs to be 2 dimensional. But you just use "np.zeros((len(X),1))" here. So I'm wondering about this. Hope for your reply. Thanks!
Hey @Huzaifg, Your code above has been really helpful. Thank you for sharing with the community. I am quite new to DeepXDE, and have a few doubts. I was wondering if you might have any answers for them.
num_domain = 30000, how many points are actually created ? Is it 30000 in each space. So since we are having a 3D problem, it would be 30000*3 or it is 30000/3 ? Hope for your reply. Thanks Hannan
- When you define
num_domain = 30000, how many points are actually created ? Is it 30000 in each space. So since we are having a 3D problem, it would be 30000*3 or it is 30000/3 ?
Hi None of the above. There will be 30000 points in your training. 30000 x and 30000 y and 30000 t. it's like: [0,0.5,0], [0.1,0.5,0.3], .....
Hello everyone,
Does anyone have any experience with plotting the above solution $T$ versus time $t$, i.e. time (t) on the x-axis and temperature (T) on the y-axis.
Thank you in advance.
@wangcj05 I actually got this to work a while back but forgot to update here. This is the equation I solved
First, I normalized the equation
And made some modifications to the boundary conditions
I also applied a output transform to ensure that the tempretures that the DNN was outputing were positive using
net.apply_output_transform(lambda x, y: abs(y))Given below is the complete code
import deepxde as dde import matplotlib.pyplot as plt import numpy as np from deepxde.backend import tf # Some useful functions t1 = 0 t2 = 1 end_time = 1 def pde(X,T): dT_xx = dde.grad.hessian(T, X ,j=0) dT_yy = dde.grad.hessian(T, X, j=1) dT_t = dde.grad.jacobian(T, X, j=2) # Dividing by rhoc to make it 1 rhoc = (3.8151 * 10**3) / (3.8151 * 10**3) kap = (385 / (3.8151 * 10**3)) # no forcing function return ((rhoc * dT_t) - (kap * (dT_xx + dT_yy))) def r_boundary(X,on_boundary): x,y,t = X return on_boundary and np.isclose(x,1) def l_boundary(X,on_boundary): x,y,t = X return on_boundary and np.isclose(x,0) def up_boundary(X,on_boundary): x,y,t = X return on_boundary and np.isclose(y,1) def down_boundary(X,on_boundary): x,y,t = X return on_boundary and np.isclose(y,0) def boundary_initial(X, on_initial): x,y,t = X return on_initial and np.isclose(t, 0) def init_func(X): x = X[:, 0:1] y = X[:, 1:2] t = np.zeros((len(X),1)) for count,x_ in enumerate(x): if x_ < 0.5: t[count] = t1 else: t[count] = t1 + (2) * (x_ - 0.5) return t def dir_func_l(X): return t1 * np.ones((len(X),1)) def dir_func_r(X): return t2 * np.ones((len(X),1)) def func_zero(X): return np.zeros((len(X),1)) def hard(X, T): x,y,t = x[:, 0:1], x[:, 1:2],x[:,2:3] return (r - r_in) * y + T_star num_domain = 30000 num_boundary = 8000 num_initial = 20000 layer_size = [3] + [60] * 5 + [1] activation_func = "tanh" initializer = "Glorot uniform" lr = 1e-3 # Applying Loss weights as given below # [PDE Loss, BC1 loss - Dirichlet Left , BC2 loss - Dirichlet Right, BC3 loss- Neumann up, BC4 loss - Neumann down, IC Loss] loss_weights = [10, 1, 1, 1, 1, 10] epochs = 10000 optimizer = "adam" batch_size_ = 256 geom = dde.geometry.Rectangle(xmin=[0, 0], xmax=[1, 1]) timedomain = dde.geometry.TimeDomain(0, end_time) geomtime = dde.geometry.GeometryXTime(geom, timedomain) bc_l = dde.DirichletBC(geomtime, dir_func_l, l_boundary) bc_r = dde.DirichletBC(geomtime, dir_func_r, r_boundary) bc_up = dde.NeumannBC(geomtime, func_zero, up_boundary) bc_low = dde.NeumannBC(geomtime, func_zero, down_boundary) ic = dde.IC(geomtime, init_func, boundary_initial) data = dde.data.TimePDE( geomtime, pde, [bc_l, bc_r, bc_up, bc_low, ic], num_domain=num_domain, num_boundary=num_boundary, num_initial=num_initial) net = dde.maps.FNN(layer_size, activation_func, initializer) net.apply_output_transform(lambda x, y: abs(y)) ## Uncomment below line to apply hard Dirichlet Boundary Conditions # net.outputs_modify(lambda x, y: x[:,0:1]*t2 + x[:,0:1] * (1 - x[:,0:1]) * y) model = dde.Model(data, net) model.compile(optimizer, lr=lr,loss_weights=loss_weights) # To save the best model every 1000 epochs checker = dde.callbacks.ModelCheckpoint( "model/model1.ckpt", save_better_only=True, period=1000 ) losshistory, trainstate = model.train(epochs=epochs,batch_size = batch_size_,callbacks = [checker]) model.compile("L-BFGS-B") dde.optimizers.set_LBFGS_options( maxcor=50, ) losshistory, train_state = model.train(epochs = epochs, batch_size = batch_size_) dde.saveplot(losshistory, trainstate, issave=True, isplot=True)The best results achieved,

I also predicted the temperature for a paticular time frame using the code given below
import matplotlib.animation as animation from matplotlib.animation import FuncAnimation ax = fig.add_subplot(111) nelx = 100 nely = 100 timesteps = 101 x = np.linspace(0,1,nelx+1) y = np.linspace(0,1,nely+1) t = np.linspace(0,1,timesteps) delta_t = t[1] - t[0] xx,yy = np.meshgrid(x,y) x_ = np.zeros(shape = ((nelx+1) * (nely+1),)) y_ = np.zeros(shape = ((nelx+1) * (nely+1),)) for c1,ycor in enumerate(y): for c2,xcor in enumerate(x): x_[c1*(nelx+1) + c2] = xcor y_[c1*(nelx+1) + c2] = ycor Ts = [] for time in t: t_ = np.ones((nelx+1) * (nely+1),) * (time) X = np.column_stack((x_,y_)) X = np.column_stack((X,t_)) T = model.predict(X) T = T*30 T = T.reshape(T.shape[0],) T = T.reshape(nelx+1,nely+1) Ts.append(T) def plotheatmap(T,time): # Clear the current plot figure plt.clf() plt.title(f"Temperature at t = {time*delta_t} unit time") plt.xlabel("x") plt.ylabel("y") plt.pcolor(xx, yy, T,cmap = 'RdBu_r') plt.colorbar() return plt def animate(k): plotheatmap(Ts[k], k) anim = animation.FuncAnimation(plt.figure(), animate, interval=1, frames=len(t), repeat=False) anim.save("trial1.gif")You can also find the gif converted to a mp4 file at the Gdrive link https://drive.google.com/file/d/1t_uWzJT6ks1uMT0EKChcw7b-HqPJGtzW/view?usp=sharing
Please do let me know if I could have done something better or some mistakes that you find, I am only starting out and would love to learn!
here if we reduce num_initial points to 400. then we get absurd result. so can you tell the approach to solve 2d heat equation with less initial points
Hello,
I tried to using DeepXDE to solve 2D time-dependent heat equations, i.e.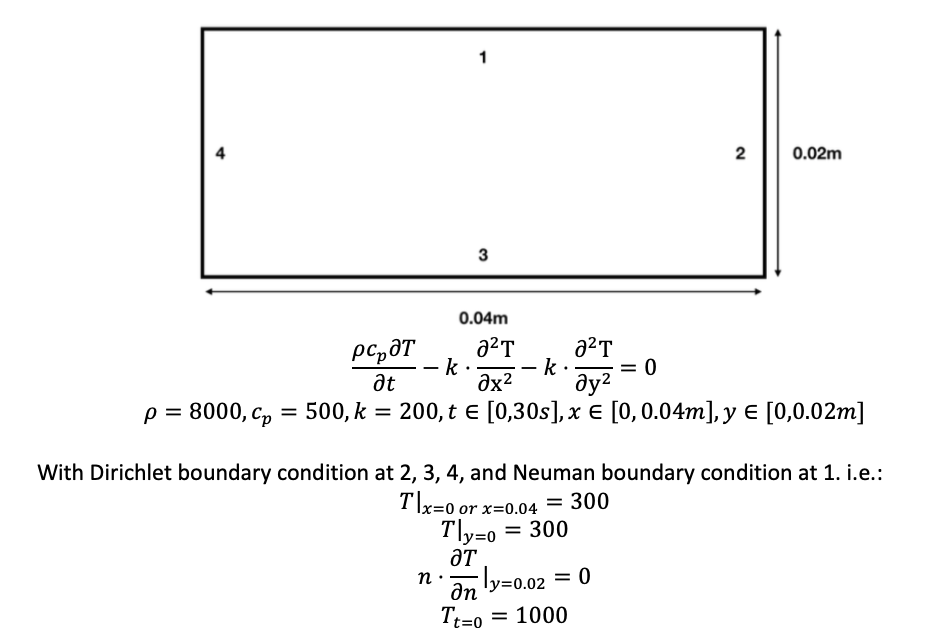
The following is my script:
However, I could not get the converged solution. Basically, the errors on the boundary are not converging. See the following:
Do you have any suggestion how to fix this problem?
Thank you in advance!