Convergence issue on Navier-Stokes equation

[inunarun]

Thanks for the great package.

I am attempting to validate / learn the framework on a simple incompressible steady state fluid mechanics problem, but seem to be having trouble with the convergence. The problem I am attempting to solve is (taken from Elmer tutorials (Tutorial 9)):

The true velocity profile from CFD is as follows:

The one I get from the neural network is: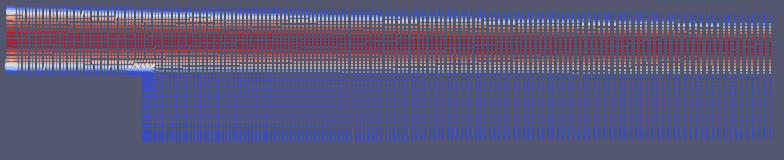

Analyzing the residuals, I see that the continuity and x-momentum residuals are at best ~1e-1 regardless of the number of epochs, network size, network architecture, etc. Would you have any recommendation on how to improve the convergence behavior?

Thanks.

My script is as follows for your reference:

from deepxde.boundary_conditions import DirichletBC
from deepxde.geometry.geometry_2d import Polygon
from deepxde.callbacks import EarlyStopping
from importlib import import_module
from deepxde.maps.fnn import FNN
from deepxde.data.pde import PDE
from deepxde.model import Model
import matplotlib.pyplot as plt
from deepxde.backend import tf
import numpy as np

def plot_points(points, color="k", marker="."):
    figure = plt.figure()
    axis = figure.add_subplot(111)
    axis.scatter(points[:, 0], points[:, 1], color=color, marker=marker)
    plt.show()

def wall_top_boundary(x, on_boundary):
    """Checks for points on top wall boundary"""
    return on_boundary and np.isclose(x[1], 2.0)

def wall_bottom_boundary(x, on_boundary):
    """Checks for points on bottom wall boundary"""
    return on_boundary and np.isclose(x[1], 0.0)

def wall_mid_horizontal_boundary(x, on_boundary):
    """Check for points on step horizontal boundary"""
    return on_boundary and (np.isclose(x[1], 1.0) and x[0] < 2.0)

def wall_mid_vertical_boundary(x, on_boundary):
    """Check for points on step horizontal boundary"""
    return on_boundary and (x[1] < 1.0 and np.isclose(x[0], 2.0))

def outlet_boundary(x, on_boundary):
    """Implements the outlet boundary with zero y-velocity component"""
    return on_boundary and np.isclose(x[0], 12.0)

def inlet_boundary(x, on_boundary):
    """Implements the inlet boundary with parabolic x-velocity component"""
    return on_boundary and np.isclose(x[0], 0.0)

def parabolic_velocity(x):
    """Parabolic velocity"""
    return (6 * (x[:, 1] - 1) * (2 - x[:, 1])).reshape(-1, 1)

def zero_velocity(x):
    """Zero velocity"""
    return np.zeros((x.shape[0], 1))

def navier_stokes(x, y):
    """Navier-Stokes equation"""
    rho = 1.0
    nu = 0.01
    eps = 1e-8

    u, v, p = y[:, 0:1], y[:, 1:2], y[:, 2:3]

    du = tf.gradients(u, x)[0]
    dv = tf.gradients(v, x)[0]
    dp = tf.gradients(p, x)[0]

    p_x, p_y = dp[:, 0:1], dp[:, 1:2]
    u_x, u_y = du[:, 0:1], du[:, 1:2]
    v_x, v_y = dv[:, 0:1], dv[:, 1:2]

    u_xx = tf.gradients(u_x, x)[0][:, 0:1]
    u_yy = tf.gradients(u_y, x)[0][:, 1:2]

    v_xx = tf.gradients(v_x, x)[0][:, 0:1]
    v_yy = tf.gradients(v_y, x)[0][:, 1:2]

    continuity = u_x + v_y + eps * p
    x_momentum = u * u_x + v * u_y + 1 / rho * p_x - nu * (u_xx + u_yy)
    y_momentum = u * v_x + v * v_y + 1 / rho * p_y - nu * (v_xx + v_yy)

    return [continuity, x_momentum, y_momentum]

if __name__ == '__main__':
    geom = Polygon([
        [0.0, 2.0], [12.0, 2.0], [12.0, 0.0], [2.0, 0.0], [2.0, 1.0],
        [0.0, 1.0]
    ])

    inlet_x = DirichletBC(geom, parabolic_velocity, inlet_boundary,
                          component=0)
    inlet_y = DirichletBC(geom, zero_velocity, inlet_boundary, component=1)
    outlet = DirichletBC(geom, zero_velocity, outlet_boundary, component=1)
    wallt_x = DirichletBC(geom, zero_velocity, wall_top_boundary, component=0)
    wallt_y = DirichletBC(geom, zero_velocity, wall_top_boundary, component=1)
    wallb_x = DirichletBC(geom, zero_velocity, wall_bottom_boundary,
                          component=0)
    wallb_y = DirichletBC(geom, zero_velocity, wall_bottom_boundary,
                          component=1)
    wallsh_x = DirichletBC(geom, zero_velocity, wall_mid_horizontal_boundary,
                           component=0)
    wallsh_y = DirichletBC(geom, zero_velocity, wall_mid_horizontal_boundary,
                           component=1)
    wallsv_x = DirichletBC(geom, zero_velocity, wall_mid_vertical_boundary,
                           component=0)
    wallsv_y = DirichletBC(geom, zero_velocity, wall_mid_vertical_boundary,
                           component=1)

    data = PDE(
        geom, navier_stokes,
        [inlet_x, inlet_y, outlet, wallb_x, wallb_y, wallsh_x, wallsh_y,
         wallsv_x, wallsv_y, pres_outlet, wallt_x, wallt_y],
        num_domain=1000, num_boundary=3000,
        num_test=5000
    )

    layer_size = [2] + [50] * 3 + [3]
    net = FNN(layer_size, "relu", "Glorot uniform",
              dropout_rate=0.1)

    model = Model(data, net)
    model.compile("adam", lr=0.001)

    early_stopping = EarlyStopping(min_delta=1e-8, patience=10000)
    model.train(epochs=25000, display_every=100,
                disregard_previous_best=True, callbacks=[early_stopping])

[lululxvi]

Here are some suggestions:

• Don't use relu, which is not second order differentiable. Use smooth activations, e.g., tanh.
• Try a small domain first.
• Don't use dropout.
• Some BCs can be imposed exactly, see "Q: By default, initial/boundary conditions are enforced in DeepXDE as soft constraints. How can I enforce them as hard constraints?" at FAQ.

[inunarun]

Thanks a lot for your recommendations. They help out a lot. Getting quite good results now. Residuals on order of ~1e-4.

It is likely I can reduce the residuals further by optimizing the network architecture.

Once more, thanks a lot for the amazing framework. It is truly revolutionary.

[jethromoses]

Hi inunarun ,

Is it possible for you to share the final code that you got working?

[inunarun]

@jethromoses: Here is the code that I gave me 1e-5 residuals. I attempted the output transforms as well, but with the output transformation, the residual was at best 1e-2. In the end, just changing the activation function and the size of the network worked for me.

Hope this helps.

from deepxde.boundary_conditions import DirichletBC
from deepxde.geometry.geometry_2d import Polygon
from tensorflow.keras.backend import set_floatx
from deepxde.callbacks import EarlyStopping
from deepxde.maps.fnn import FNN
from deepxde.data.pde import PDE
from deepxde.model import Model
from deepxde.backend import tf
import numpy as np

set_floatx("float64")

def wall_top_boundary(x, on_boundary):
    """Checks for points on top wall boundary"""
    return on_boundary and np.isclose(x[1], 2.0)

def wall_bottom_boundary(x, on_boundary):
    """Checks for points on bottom wall boundary"""
    return on_boundary and np.isclose(x[1], 0.0)

def wall_mid_horizontal_boundary(x, on_boundary):
    """Check for points on step horizontal boundary"""
    return on_boundary and (np.isclose(x[1], 1.0) and x[0] < 2.0)

def wall_mid_vertical_boundary(x, on_boundary):
    """Check for points on step horizontal boundary"""
    return on_boundary and (x[1] < 1.0 and np.isclose(x[0], 2.0))

def outlet_boundary(x, on_boundary):
    """Implements the outlet boundary with zero y-velocity component"""
    return on_boundary and np.isclose(x[0], 12.0)

def inlet_boundary(x, on_boundary):
    """Implements the inlet boundary with parabolic x-velocity component"""
    return on_boundary and np.isclose(x[0], 0.0)

def parabolic_velocity(x):
    """Parabolic velocity"""
    return (6 * (x[:, 1] - 1) * (2 - x[:, 1])).reshape(-1, 1)

def zero_velocity(x):
    """Zero velocity"""
    return np.zeros((x.shape[0], 1))

def output_transformer(inputs, outputs):
    """Apply output transforms to strictly enforce boundary conditions"""

    top_line = inputs[:, 1] - 2.0
    bottom_line = inputs[:, 1]
    mid_hor_line = inputs[:, 1] - 1.0
    mid_ver_line = inputs[:, 0] - 2.0
    outlet_line = inputs[:, 0] - 12.0
    inlet_line = inputs[:, 0]
    # velocity_profile = 6.0 * (inputs[:, 1] - 1.0) * (2.0 - inputs[:, 1])
    velocity_profile = 1.0

    u_multiplier = (top_line * bottom_line * mid_hor_line * mid_ver_line *
                    velocity_profile)
    v_multiplier = (top_line * bottom_line * mid_hor_line * mid_ver_line *
                    outlet_line * inlet_line)
    p_multiplier = 1.0

    return tf.transpose(
        tf.stack((
            u_multiplier * outputs[:, 0],
            v_multiplier * outputs[:, 1],
            p_multiplier * outputs[:, 2]
        ))
    )

def navier_stokes(x, y, X):
    """Navier-Stokes equation"""
    rho = 1.0
    nu = 0.01
    eps = 1e-8

    u, v, p = y[:, 0:1], y[:, 1:2], y[:, 2:3]

    du = tf.gradients(u, x)[0]
    dv = tf.gradients(v, x)[0]
    dp = tf.gradients(p, x)[0]

    p_x, p_y = dp[:, 0:1], dp[:, 1:2]
    u_x, u_y = du[:, 0:1], du[:, 1:2]
    v_x, v_y = dv[:, 0:1], dv[:, 1:2]

    u_xx = tf.gradients(u_x, x)[0][:, 0:1]
    u_yy = tf.gradients(u_y, x)[0][:, 1:2]

    v_xx = tf.gradients(v_x, x)[0][:, 0:1]
    v_yy = tf.gradients(v_y, x)[0][:, 1:2]

    continuity = u_x + v_y + eps * p
    x_momentum = u * u_x + v * u_y + 1 / rho * p_x - nu * (u_xx + u_yy)
    y_momentum = u * v_x + v * v_y + 1 / rho * p_y - nu * (v_xx + v_yy)

    return [continuity, x_momentum, y_momentum]

if __name__ == '__main__':
    """
    Geometry
    --------
             (0, 2)       (12, 2)
              *------------*
        in -> |            |
        (0, 1)*--*(2,1)    . -> out
                 |         |
            (2,0)*---------*(12, 0)
    """
    geom = Polygon([
        [0.0, 2.0], [12.0, 2.0], [12.0, 0.0], [2.0, 0.0], [2.0, 1.0],
        [0.0, 1.0]
    ])

    inlet_x = DirichletBC(geom, parabolic_velocity, inlet_boundary,
                          component=0)
    inlet_y = DirichletBC(geom, zero_velocity, inlet_boundary, component=1)
    outlet = DirichletBC(geom, zero_velocity, outlet_boundary, component=1)
    wallt_x = DirichletBC(geom, zero_velocity, wall_top_boundary, component=0)
    wallt_y = DirichletBC(geom, zero_velocity, wall_top_boundary, component=1)
    wallb_x = DirichletBC(geom, zero_velocity, wall_bottom_boundary,
                          component=0)
    wallb_y = DirichletBC(geom, zero_velocity, wall_bottom_boundary,
                          component=1)
    wallsh_x = DirichletBC(geom, zero_velocity, wall_mid_horizontal_boundary,
                           component=0)
    wallsh_y = DirichletBC(geom, zero_velocity, wall_mid_horizontal_boundary,
                           component=1)
    wallsv_x = DirichletBC(geom, zero_velocity, wall_mid_vertical_boundary,
                           component=0)
    wallsv_y = DirichletBC(geom, zero_velocity, wall_mid_vertical_boundary,
                           component=1)

    data = PDE(
        geom, navier_stokes,
        [inlet_x, inlet_y, outlet, wallt_x, wallt_y, wallb_x,
         wallb_x, wallsh_x, wallsh_y, wallsv_x, wallsv_y], num_domain=10000,
        num_boundary=10000, num_test=10000
    )

    layer_size = [2] + [50] * 6 + [3]
    net = FNN(layer_size, "tanh", "Glorot uniform")
    # net.apply_output_transform(output_transformer)

    model = Model(data, net)
    model.compile("adam", lr=0.001)

    early_stopping = EarlyStopping(min_delta=1e-8, patience=40000)
    model.train(epochs=80000, display_every=1000, callbacks=[early_stopping],
                disregard_previous_best=True)

[sumantkrsoni]

Hello @jethromoses How much time generally it took for 80000 iterations?

[sumantkrsoni]

Why, in PDE definition wallb_x appears twice,

data = PDE( geom, navier_stokes, [inlet_x, inlet_y, ... wallb_x,wallb_x, .... wallsv_x, wallsv_y], .........., num_test=10000 )

I think, it must be: data = PDE( geom, navier_stokes, [inlet_x, inlet_y, ... wallb_x, wallb_y , .... wallsv_x, wallsv_y], .........., num_test=10000 )

Also, could you (@lululxvi ) please suggest me,

• after enforcing the exact boundary condition, the maximum columns of BC in the training process become zero. Why is it so? & Is it obvious after enforcing the exact BC?

[lululxvi]

Maybe wallb_x is just a typo.

Enforcing the exact boundary condition means the corresponding loss is 0.

[sumantkrsoni]

Thanks @lululxvi

[ghost]

Hi, i have a question about the implementation of the continuity equation:

continuity = u_x + v_y + eps * p

why do you consider the pressure in there? i know that the eps parameter is very small but it doesn't make much sense to me.

Thanks!

[inunarun]

it is in order to introduce numerical stability. since we are operating with differential operators in a discretized environment, there are usually more local instabilities which is not an issue in CFD. although, I don't think it impacts this particular case too much as it is laminar flow.

[ghost]

@inunarun thanks for your answer! so you think it's important to have the pressure there if i'm working with more turbulent flows?

also, there is an article talking about introducing numerical stability this way? or it's a conclusion about your own experience programming PINN's?

[hchoiz]

How could I impose "pressure=0" and "du/dy=0" boundary conditions simultaneously at the exit?

[lululxvi]

@hchoiz You simply write two BCs for these two.

[hchoiz]

Dear lulu,

I appreciate your quick response.^^

As following line, I guess the component should be '2' for pressure condition. Am I correct?

outlet1 = DirichletBC(geom, zero_pressure, outlet_boundary, component=2) outlet2 = DirichletBC(geom, zero_velocity, outlet_boundary, component=1)

def zero_pressure(x): return np.zeros((x.shape[0], 1))

Thank you.

[lululxvi]

Yes.

[SimonZeng7108]

@inunarun @lululxvi Dear OP and Author,

I tried to add a simple hole in the geometry, but the performance is rather poor. Please see the images attached below. The velocity field doesn't look right as the flow should pass by the hole, otherwise, the momentum equation will not be met. However, when I look at the residual of the whole domain, it is relatively very low everywhere, which does not make sense as the momentum loss term should be quite high(Although the residual map is the average of all loss terms). I wonder what may cause this issue.

Velocity

Residual

#https://github.com/lululxvi/deepxde/issues/80

from deepxde.icbc import DirichletBC
from deepxde.geometry.geometry_2d import Polygon
from deepxde.callbacks import EarlyStopping
from deepxde.nn import FNN
from deepxde.data.pde import PDE
from deepxde.model import Model
from deepxde.backend import tf
import numpy as np
import deepxde as dde
import matplotlib.pyplot as plt
import torch

def wall_top_boundary(x, on_boundary):
    """Checks for points on top wall boundary"""
    return on_boundary and np.isclose(x[1], 2.0)

def wall_bottom_boundary(x, on_boundary):
    """Checks for points on bottom wall boundary"""
    return on_boundary and np.isclose(x[1], 0.0)

def wall_mid_horizontal_boundary(x, on_boundary):
    """Check for points on step horizontal boundary"""
    return on_boundary and (np.isclose(x[1], 1.0) and x[0] < 2.0)

def wall_mid_vertical_boundary(x, on_boundary):
    """Check for points on step horizontal boundary"""
    return on_boundary and (x[1] < 1.0 and np.isclose(x[0], 2.0))

def outlet_boundary(x, on_boundary):
    """Implements the outlet boundary with zero y-velocity component"""
    return on_boundary and np.isclose(x[0], 12.0)

def inlet_boundary(x, on_boundary):
    """Implements the inlet boundary with parabolic x-velocity component"""
    return on_boundary and np.isclose(x[0], 0.0)

def boundary_circle(x, on_boundary):
    #centre (4, 1), radius 0.3
    return on_boundary and disk_domain.on_boundary(x)

def parabolic_velocity(x):
    """Parabolic velocity"""
    return (6 * (x[:, 1] - 1) * (2 - x[:, 1])).reshape(-1, 1)

def zero_velocity(x):
    """Zero velocity"""
    return np.zeros((x.shape[0], 1))

def navier_stokes(x, u):
    #x - x, y coordinates
    #u - u, v, p
    rho = 1
    mu = 0.01
    eps = 1e-8
    u_vel, v_vel, p = u[:, 0:1], u[:, 1:2], u[:, 2:]
    u_vel_x = dde.grad.jacobian(u, x, i=0, j=0)
    u_vel_y = dde.grad.jacobian(u, x, i=0, j=1)
    u_vel_xx = dde.grad.hessian(u, x, component=0, i=0, j=0)
    u_vel_yy = dde.grad.hessian(u, x, component=0, i=1, j=1)

    v_vel_x = dde.grad.jacobian(u, x, i=1, j=0)
    v_vel_y = dde.grad.jacobian(u, x, i=1, j=1)
    v_vel_xx = dde.grad.hessian(u, x, component=1, i=0, j=0)
    v_vel_yy = dde.grad.hessian(u, x, component=1, i=1, j=1)

    p_x = dde.grad.jacobian(u, x, i=2, j=0)
    p_y = dde.grad.jacobian(u, x, i=2, j=1)

    momentum_x = (
        rho * (u_vel * u_vel_x + v_vel * u_vel_y) + p_x - mu * (u_vel_xx + u_vel_yy)
    )
    momentum_y = (
        rho * (u_vel * v_vel_x + v_vel * v_vel_y) + p_y - mu * (v_vel_xx + v_vel_yy)
    )
    continuity = u_vel_x + v_vel_y

    return [momentum_x, momentum_y, continuity]

def output_transformer(inputs, outputs):
    """Apply output transforms to strictly enforce boundary conditions"""

    top_line = inputs[:, 1] - 2.0
    bottom_line = inputs[:, 1]
    mid_hor_line = inputs[:, 1] - 1.0
    mid_ver_line = inputs[:, 0] - 2.0
    outlet_line = inputs[:, 0] - 12.0
    inlet_line = inputs[:, 0]
    velocity_profile = 6.0 * (inputs[:, 1] - 1.0) * (2.0 - inputs[:, 1])
    # velocity_profile = 1.0

    u_multiplier = (top_line * bottom_line * mid_hor_line * mid_ver_line *
                    velocity_profile)
    v_multiplier = (top_line * bottom_line * mid_hor_line * mid_ver_line *
                    outlet_line * inlet_line)
    p_multiplier = 1.0

    return torch.cat([(u_multiplier * outputs[:, 0]).reshape(-1, 1), (v_multiplier * outputs[:, 1]).reshape(-1, 1), (p_multiplier * outputs[:, 2]).reshape(-1, 1)], dim=1)

if __name__ == '__main__':
    """
    Geometry
    --------
                (0, 2)       (12, 2)
                  *------------*
        in -> |            |
        (0, 1)*--*(2,1)    . -> out
                    |         |
            (2,0)*---------*(12, 0)
    """
    geom = Polygon([
        [0.0, 2.0], [12.0, 2.0], [12.0, 0.0], [2.0, 0.0], [2.0, 1.0],
        [0.0, 1.0]
    ])
    disk_domain = dde.geometry.Disk([4, 1], 0.3)
    geom = geom - disk_domain

    inlet_x = DirichletBC(geom, parabolic_velocity, inlet_boundary,
                          component=0)
    inlet_y = DirichletBC(geom, zero_velocity, inlet_boundary, component=1)
    outlet = DirichletBC(geom, zero_velocity, outlet_boundary, component=1)
    wallt_x = DirichletBC(geom, zero_velocity, wall_top_boundary, component=0)
    wallt_y = DirichletBC(geom, zero_velocity, wall_top_boundary, component=1)
    wallb_x = DirichletBC(geom, zero_velocity, wall_bottom_boundary,
                          component=0)
    wallb_y = DirichletBC(geom, zero_velocity, wall_bottom_boundary,
                          component=1)
    wallsh_x = DirichletBC(geom, zero_velocity, wall_mid_horizontal_boundary,
                           component=0)
    wallsh_y = DirichletBC(geom, zero_velocity, wall_mid_horizontal_boundary,
                           component=1)
    wallsv_x = DirichletBC(geom, zero_velocity, wall_mid_vertical_boundary,
                           component=0)
    wallsv_y = DirichletBC(geom, zero_velocity, wall_mid_vertical_boundary,
                           component=1)
    circle = DirichletBC(geom, zero_velocity, boundary_circle)

    data = PDE(
        geom, navier_stokes,
        [inlet_x, inlet_y, outlet, wallt_x, wallt_y, wallb_x,
        wallb_x, wallsh_x, wallsh_y, wallsv_x, wallsv_y, circle], num_domain=50000,
        num_boundary=50000, num_test=10000
    )

    layer_size = [2] + [50] * 6 + [3]
    net = FNN(layer_size, "tanh", "Glorot uniform")
    # net.apply_output_transform(output_transformer)

    model = Model(data, net)
    model.compile("adam", lr=0.001)

    # early_stopping = EarlyStopping(min_delta=1e-8, patience=40000)
    checker = dde.callbacks.ModelCheckpoint("model/bend_model.ckpt", save_better_only=True, period=1000)
    # model.train(iterations=5000, display_every=1000, callbacks=[checker])

    model.compile("L-BFGS")
    # losshistory, train_state = model.train(model_save_path = "./model/bend_model.ckpt")

    model.restore("model/bend_model.ckpt-20000.pt", verbose=1)  # Replace ? with the exact filename
    X = geom.random_points(100000)
    output = model.predict(X)

    u_pred = output[:, 0]
    v_pred = output[:, 1]
    velocity_pred = np.sqrt(u_pred**2 + v_pred**2)
    p_pred = output[:, 2]

    fig = plt.figure(figsize=(12,2))
    plt.scatter(X[:, 0], X[:, 1], c=velocity_pred, cmap='jet',vmin=0, vmax=1, marker = '.')
    plt.colorbar().ax.set_ylabel('z', rotation=270)

    #residual plot 
    f = model.predict(X, operator=navier_stokes)
    print("f shape:", f[0].shape)

    fig = plt.figure(figsize=(12,2))
    plt.scatter(X[:, 0], X[:, 1], c=f[0], cmap='jet',vmin=0, vmax=1, marker = '.')
    plt.colorbar().ax.set_ylabel('z', rotation=270)
    plt.show()

    residual = np.mean(np.absolute(f))

    print("Mean residual:", residual)

[ghost]

Hello @lululxvi , how can I implement for DeepONets this code navier-stokes?